滲透數學思想于課堂

姜炅祺 劉君

【摘要】初中是學生發展的重要階段，如何將數學思想滲透在教學之中，培養學生應用數學思想解決數學問題，將所學知識內化，是每一位教師需要思考的問題.本文從“完全平方公式”這一教學課例出發，探討如何在數學課堂的教學中滲透數學思想.

【關鍵詞】數學思想;完全平方公式;教學方法

一、引 言

所謂數學思想，是指現實世界的空間形式和數量關系反映到人們的意識之中，經過思維活動而產生的結果.數學思想是對數學事實與理論經過概括后產生的本質認識，在整個數學教學過程中，數學思想方法的傳授應是每個數學教師重要的授課內容之一.數學思想方法是數學的精髓，是數學素養的重要構成之一，只有讓學生領會了數學思想方法，學生才能有效地應用知識，并形成能力.

“數與代數”在數學教學中占有重要地位，完全平方公式是其中因式分解的一個重要分支，是整式乘法的重點內容，也是初中階段學生學習分式、一元二次方程、二次函數等知識的基礎，應用十分廣泛.

筆者在教學中發現，不同的教師對于完全平方公式的授課處理方式都有所不同.怎樣讓學生經歷獲得及提煉的過程，感悟其作為公式的合理性，體會其中所蘊含的數學思想，并在深入理解基礎上靈活運用，這是教師教學研究的重點.

二、在新授課程中滲透數學思想

（一）幾何直觀思想的滲透

幾何直觀是指憑借圖形的直觀性特點將抽象的數學語言與直觀的圖形語言有機地結合起來，即將抽象思維同形象思維結合起來，充分展現問題的本質，突破數學理解上的難點.

在完全平方公式的新授教學過程中，很多教師采用幾何直觀的方式將完全平方公式展現給學生，以此方法引入能使學生對于完全平方公式有直觀的了解.

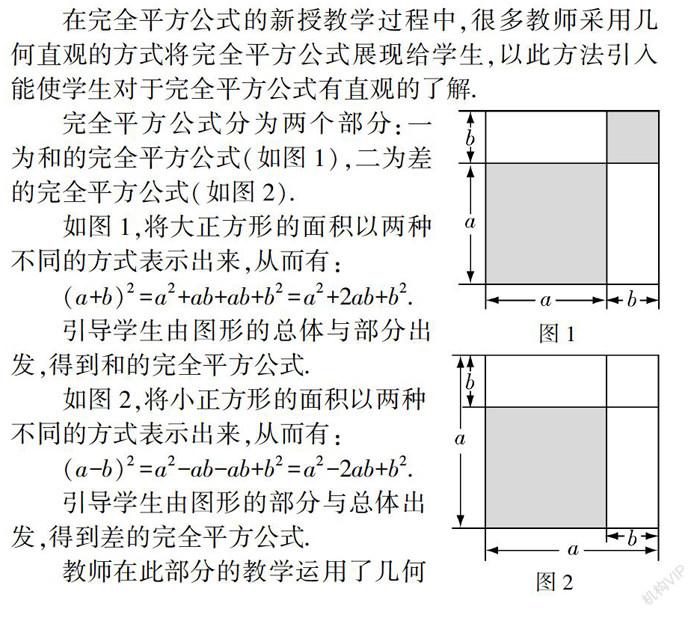
圖2完全平方公式分為兩個部分：一為和的完全平方公式（如圖1），二為差的完全平方公式（如圖2）.

如圖1，將大正方形的面積以兩種不同的方式表示出來，從而有：

（a+b）2=a2+ab+ab+b2=a2+2ab+b2.

引導學生由圖形的總體與部分出發，得到和的完全平方公式.

如圖2，將小正方形的面積以兩種不同的方式表示出來，從而有：

（a-b）2=a2-ab-ab+b2=a2-2ab+b2.

引導學生由圖形的部分與總體出發，得到差的完全平方公式.

圖3教師在此部分的教學運用了幾何直觀思想.當然，在完全平方公式的綜合應用中，也可以運用幾何直觀的思想解決.如圖3，外圍由四個長為a、寬為b的矩形圍成，那么中間小正方形的邊長即為（a-b），從而大正方形的面積也有兩種方式表示，聯立可得：

（a+b）2=（a-b）2+4ab.

教師在課堂上滲透幾何直觀的數學思想方法，將完全平方公式這樣的代數形式轉化為直觀上的幾何圖形，幾何直觀的數學思想滲透在教學過程中，達到了良好的教學效果.

誠然，光有幾何直觀上的教學方法是遠遠不夠的，還需要回歸本質.在人教版第十四章的第一節，學生已經學習到了整式乘法的一般性質，教師可以引導學生運用多項式與多項式相乘的性質得到結論.

在此方面，不同教師處理的方式也有所不同，也滲透了多種數學思想.

（二）從一般到特殊思想的滲透

從一般到特殊思想是指在理論指導下，用已有的規律解決此類事物中的新問題的過程.

在完全平方公式這節課的教學過程中，有的教師從引導學生回憶多項式的乘法的運算法則、運算的依據出發，讓學生自行計算（x+b）（x+d），學生可以利用公式直接寫出結果，同時，學生在討論時發現，這是（a+b）（c+d）在a=c=x時候的特殊情況.由此出發，讓學生再進行自由討論：你認為在（a+b）（c+d）=ac+ad+bc+bd中，還有哪些特殊情形？你能得到什么？教師此時完全放手讓學生探究.學生由于采用方法不同，經過討論可得出的結論也多種多樣.

在這個過程中，教師向學生滲透了從一般到特殊的數學思想，引導學生在多項式乘法基礎上探究特例，使學生通過自己的探究與討論發現完全平方公式的發展過程和內在的邏輯線索，符合學生的認知規律.

（三）從特殊到一般思想的滲透

從特殊到一般的思想是指通過列舉特殊情況來找到共同點，從而總結規律并將規律推廣到所有情況.

在完全平方公式的教學中，由于學生已經學習了多項式的乘法法則，所以，有些教師在新授課程中直接舉出一些例子，讓學生自己進行計算，一步步地引導學生掌握完全平方公式.滲透從特殊到一般的思想，以培養學生歸納演繹的能力.

教師先引出了一系列的問題：請同學們計算下列各式，從中你能發現什么規律？

①（m+2）2=（m+2）m+2=;

②（2x+3y）2=;

③（m-2）2=.

經過學生討論后，教師將情況推廣到一般，引導學生歸納得出運算公式，并探討完全平方公式的特征，用語言進行描述.

學生在學習乘法公式前已經學習了多項式的乘法運算，兩個完全相同的多項式相乘在計算和實際應用中較為常見.在此課中，教師先讓學生自己進行兩個完全相同的多項式相乘的運算，并總結發現規律，最后推廣歸納一般結論——完全平方公式.學生真正經歷了由特殊到一般的思想過程，其歸納演繹的能力得到了培養.

（四）比較思想的滲透

比較思想是指抓住定義中的相似的特征進行比較，有利于學生進行歸納和記憶.

在講解完完全平方公式的課程后需要總結完全平方公式的特點，教師引導學生通過觀察、比較公式（a+b）2=a2+2ab+b2與（a-b）2=a2-2ab+b2的關系，進行總結它們的共同特點：①二次三項式;②首末是平方項;③中間項是首末項底數積的2倍;二者的區別是前者是兩數和的平方加上乘積的2倍，后者是兩數和的平方減去乘積的2倍.教師用語言分析完后還可以框架的形式進行總結，進一步突出公式的特征.