一類非均勻傳輸逆散射問題的混合交互關系研究

葉建國

(喀什大學數學與統計學院，新疆喀什 844000)

0 引言

在逆散射問題中，交互關系刻畫了散射場或遠場的某種對稱性（包括散射場與散射場、散射場與遠場、遠場與遠場），通過交互關系，在數學上揭示了交換源（source）和接收器（receiver）的角色的合理性[1-2].混合交互關系在傳輸逆散射問題的理論研究中起著非常重要的作用，如在礦產資源的勘探、材料的無損檢測、醫學成像、雷達和聲吶的探測等實際應用中，當目標障礙物或介質有一部分無法使用接收器搜集數據時，必須通過混合交互關系來簡化問題[3-6].本文研究了一類帶有傳導邊界條件的非均勻傳輸逆散射問題的混合交互關系，并給出問題對應的Green函數的遠場G∞與全場u、穿透場v的交互關系刻畫，為重構散射體做好理論準備.

1 問題的描述

設可穿透障礙物Ω∈?3為開的單連通區域具有C2邊界S.設障礙物Ω內外介質不一樣且表面涂有阻抗率為λ＞0 電導涂層,電場極化為TM 模式,當入射方向為d∈S2?{x∈?3：|x|=1}的入射平面波ui=eik0x·d遇到電介質時,在介質的邊界?Ω產生傳導邊界條件,記該非均勻可穿透散射問題的模型可用全場u和穿透場v的Helmholtz方程的傳導邊值問題描述為

其中：波數kj＞0（j=0，1），傳輸系數η＞0 為Ω內外介質密度比，n 表示邊界S的外單位法向量，i=全場u?ui+us是給定的入射場ui和與之相應的散射場us之和，“±”表示x沿法線方向n從Ω的外（內）逼近邊界S.此外，假設散射場us滿足Sommerfeld衰減條件[1]

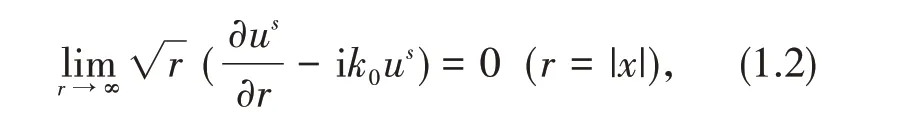
滿足衰減條件（1.2）的Helmholtz 方程的解稱為輻射解（radiating solution）.當|x|→∞時，散射場us(x)有出射球面波（outgoing spherical wave）漸近表示

傳導邊值問題（1.1）—（1.2）的適定性鄧霞等在文獻[7]中應用積分方程的方法已經研究，文獻[8]研究了該問題邊值算子的非單射性.

2 混合交互關系

設G(x，y)是問題（1.1）—（1.2）對應的Green函數[8]，則G(x，y)滿足邊值問題

綜合（1）和（2），定理得證.

注2：由文獻[9]—[11]可知，表示式（2.9）和（2.14）可以由經典的Green 表示公式中的基本解Φj(x,y)換成問題對應的Green 函數G得到.事實上，基本解Φj(x,y)是Helmholtz 方程的特殊Green函數.