帶時變高階矩的已實現GAS 模型及其實證研究

吳鑫育,王海運

（安徽財經大學 金融學院，安徽 蚌埠 233030）

0 引言

波動率在衍生產品定價、資產配置以及風險管理等眾多金融應用中發揮著重要的作用.因此，波動率建模和預測一直是金融計量經濟學研究的焦點和熱點.傳統上，學者們最常使用GARCH 模型[1]和隨機波動率模型[2]對資產收益率的動態性建模.由于波動率具有不可觀測性，通常將波動率看作是時變參數引入到模型中，因此，GARCH 模型和隨機波動率模型又被看作是時變參數模型.Creal 等[3]將時變參數模型分為觀測驅動（obervation-driven）模型和參數驅動（pa‐rameter-driven）模型.參數驅動模型參數的時變性通過一階自回歸過程描述，參數估計時通常需要借助模擬方法進行計算，模型的估計較為復雜，隨機波動率模型屬于參數驅動模型.觀測驅動模型參數的時變性基于過去的信息驅動，簡化了似然估計，模型可以直接使用極大似然方法估計.因此，觀測驅動模型在對波動率的動態性進行建模與應用時受到學者的青睞，GARCH 模型即屬于觀測驅動模型.

Creal 等[3]和Harvey[4]將觀測驅動模型與時變參數的得分函數相結合，構建了廣義自回歸得分（gener‐alized autoregressive score，GAS）模 型.GAS 模 型 將 條 件密度函數得分作為時變參數的主要驅動，能夠充分利用觀測變量條件分布的信息，與此同時，具備其他觀 測 驅 動 模 型 優 點.Creal 等[5]、Lucas 等[6]和Harvey[4]和Luati[7]驗證了GAS 模型在金融市場中應用的有效性.后續一些學者對GAS 模型進行擴展并運用到金融實踐中[8-10].

一些學者基于GAS 模型框架，構建了時變波動率模型，例如Creal 等[11]、Blasques[12]以及Nystrup[13].國內學者對GAS 波動率模型的相關研究還較為少見，例如姚萍等人[14]的研究.傳統GAS 模型與GARCH 模型相同，利用日度收盤價數據對波動率模型進行建模，忽略了日內價格變動的信息，從而影響波動率估計的準確性.隨著計算機技術與信息儲存技術的發展，利用日內高頻數據對波動率建模受到了學者們的廣泛關注.例如Hansen 等[15]提出了已實現GARCH 模型，Koopman 和Scharth[16]提出已實現隨機波動率模型，Hansen 和Huang[16]提出了已實現EGARCH（REGARCH）模型，但是這些模型都未能充分利用觀測變量條件分布的信息.基于此，一些學者基于GAS 模型引入日內高頻數據.Opschoor 等[18]將已實現測度引入HEAVY GAS 模型，提出了一個新的多元波動率模型；Hansen等[19]基于得分驅動框架構建了已實現Wishart-GARCH模型.在國內，王天一和黃卓[20]將GAS 模型框架引入厚尾已實現GARCH 模型，提出了已實現GAS-GARCH（RGAS-GARCH）模型，沈根祥和鄒欣悅[21]提出了RGAS-HEAVY 模型；上述研究表明引入已實現測度的GAS 模型相對于傳統已實現波動率模型具有更好的實證效果.

然而，上述研究還沒有將高階矩特征納入波動率模型中，Amaya 等[22]、Do 等[23]和Shen[24]的研究表明，考慮高階矩特征有助于提升資產收益率預測的精確性.最近，朱鵬飛[25]提出了集成EEMD-SJC Copula-GARCHSK 套期保值比率估計模型，研究表明引入高階矩后的套期保值模型具有更好的參數估計效果.上述研究中高階矩被當作常數納入模型中，越來越多的研究表明高階矩具有時變性.León[26]、王鵬[27]以及呂永健和王鵬[28]的研究表明考慮高階矩的時變性能更好地測度金融市場風險.同時考慮已實現測度以及高階矩時變性的研究較為少見，Wu[29]提出了REGARCH-SK 模型.上述研究表明，對于資產收益率序列表現出尖峰厚尾特征的金融市場，考慮時變高階矩能夠更有效地預測風險值.但是，這些研究未能充分利用觀測變量條件分布的信息，且對極端值的預測不夠穩健.

鑒于此，本文結合GAS 模型框架，對資產收益率以及已實現測度聯合建模，假設金融資產收益率服從時變學生t分布，構建能夠捕獲時變高階矩特征的TVPRGAS 波動率模型.模型同時引入已實現測度，能夠更好地利用價格變動包含的日內信息.TVP-RGAS 波動率模型通過對時變參數得分函數的設定，能夠充分利用觀測變量條件分布信息，且對極端值的預測較為穩健.由于該模型屬于觀測驅動模型，可用極大似然方法直接估計參數，模型具有易于實現的優點.本文采用上證綜合指數，對TVP-RGAS 波動率模型進行實證研究，與其他已實現波動率模型在條件方差預測以及VaR 預測上進行實證比較分析.

1 模型構建

TVP-RGAS 波動率模型對資產收益率rt和對數已實現測度xt聯合建模：

其中，μ表示資產收益率的條件均值，σt表示資產收益率的條件波動率，zt表示與度量誤差ut相互獨立標準化的信息.Zhu 和Galbraith[30]、楊興林和王鵬[31]研究發現學生t分布能夠很好地捕獲資產收益率序列的尖峰厚尾特征.因此，本文假設rt服從學生t分布.對于已實現測度，本文使用Hansen等[32]在已實現GARCH 中使用的方法，假定對數已實現測度xt服從正態分布，可以得到rt和xt的條件概率密度函數為：

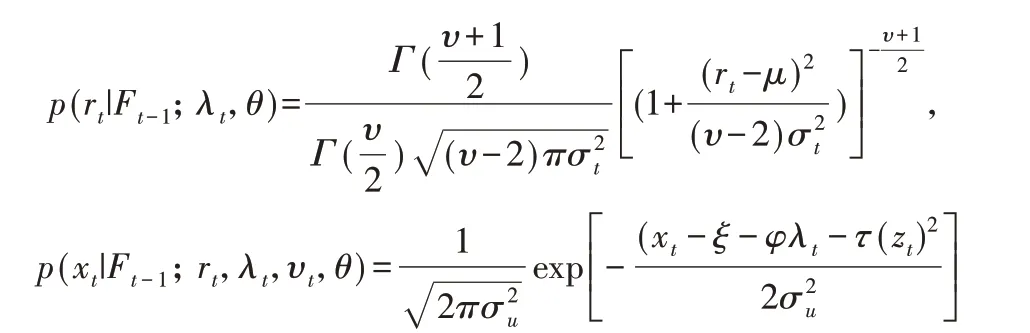
已有大量研究表明，波動率以及高階矩具有時變性[32,33].此 外，Gómez[34]以 及Lacus 等[35]驗 證 了 學 生t分布的自由度υ（υ＞2）是時變的.因此，除了假設波動率是時變的，本文還假設自由度參數υt也是時變的.

為了刻畫時變波動率以及時變自由度參數的動態性，本文采用Creal 等[3]提出的GAS 得分框架.具體地，令ft=(f1，t，f2，t)'，其中f1，t=λt，υt=2+exp(f2，t).在此設定下可以確保時變參數υt＞2，因此學生t分布的方差總是存在，時變參數ft基于GAS 模型框架下的動態性為：

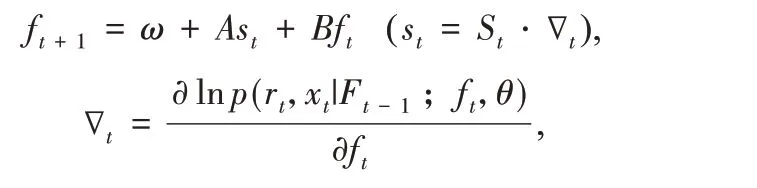
其中，參數A表示時變參數對得分新息的反應，參數B表示時變參數的持續性，st是條件分布的得分，St是標度矩陣.本文使用Russell 和Engle[36]在得分驅動模型中設定標度矩陣的方法，假設St=I，I是一個單位矩陣.lt是rt和xt的對數聯合條件概率密度函數，Ft-1是t-1 時刻可觀測的信息集，θ是非時變參數向量.可以看到，GAS 框架對時變參數動態性的設定充分利用了條件分布的信息，保證了模型設定的合理性.

由此，可以得到時變參數f1，t以 及f2，t的動態過程為：

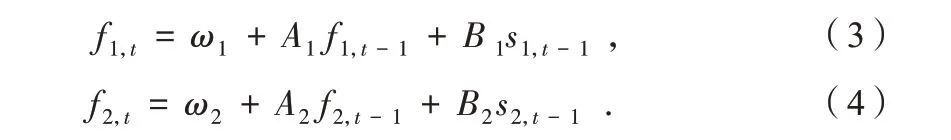
據此可以得到時變參數f1，t以 及f2，t的得分s1，t以及s2，t為：

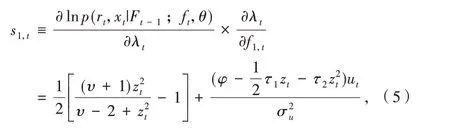
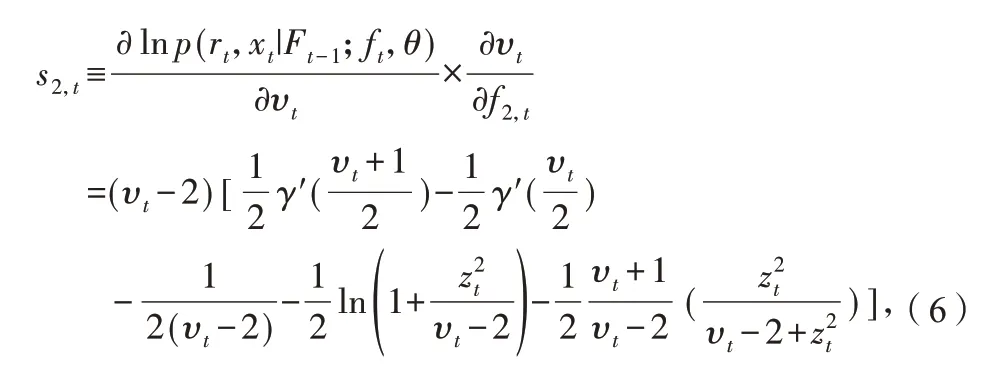
其中，γ(υ)=lnΓ(υ).

方程（1）-（6）即構成TVP-RGAS 波動率模型.TVPRGAS 波動率模型對資產收益率和已實現測度聯合建模，引入已實現測度充分利用資產收益率日內變動信息，同時可以捕獲時變高階矩信息，是一個較為靈活的模型.通過約束A2=B2=0，此時時變參數υ變為常數，TVP-RGAS 波動率模型退化成帶常數高階矩的RGAS 波動率模型，進一步令ω2=0 得到不包含高階矩信息的RGAS 波動率模型.

由于TVP-RGAS 波動率模型屬于觀測驅動模型，具有易于實現的特點，可用極大似然方法直接估計參數.其對數似然函數的形式如下：

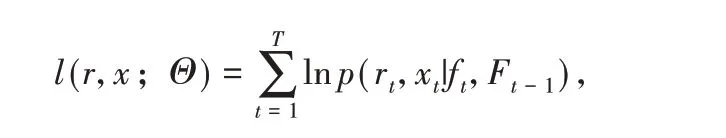
其中，Θ是模型的參數向量，通過最大化似然函數可得到TVP-RGAS 波動率模型參數的極大似然估計

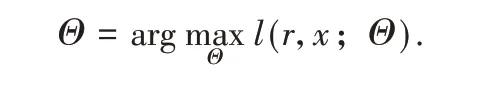
2 實證分析

2.1 數 據

本文選取上證綜合指數（SSE）從2005 年1 月4 日至2020 年9 月30 日共3642 個交易日的5 分鐘高頻交易價格數據和日收盤價數據進行實證分析.所有數據均來源于wind 資訊.

定義第t個交易日的指數收益率為rt=pt-pt-1，其中pt是第t交易日的指數對數收盤價格.本文選取已實現方差作為已實現測度，其優勢是可以充分利用高頻數據所包含的日內信息，使模型可以更好地擬合數據.然而，實際中由于受到非交易時間和微觀結構噪聲的影響，RV 往往是真實日度波動率的有偏估計，需要進行偏差修正.

表1 給出了上證綜合指數的日度指數資產收益率rt以及對數已實現測度log(RVt)的描述性統計量.從表1的結果來看，上證綜合指數的日度指數資產收益率rt的均值大于0，偏度小于0，峰度大于3，呈現出左偏以及尖峰厚尾特征.Jarque-Bera 統計量顯著，拒絕其為正態性的假定.上證綜合指數的對數已實現方差log(RVt)的偏度接近于0，峰度接近于3，Jarque-Bera統計值接近于正態分布.

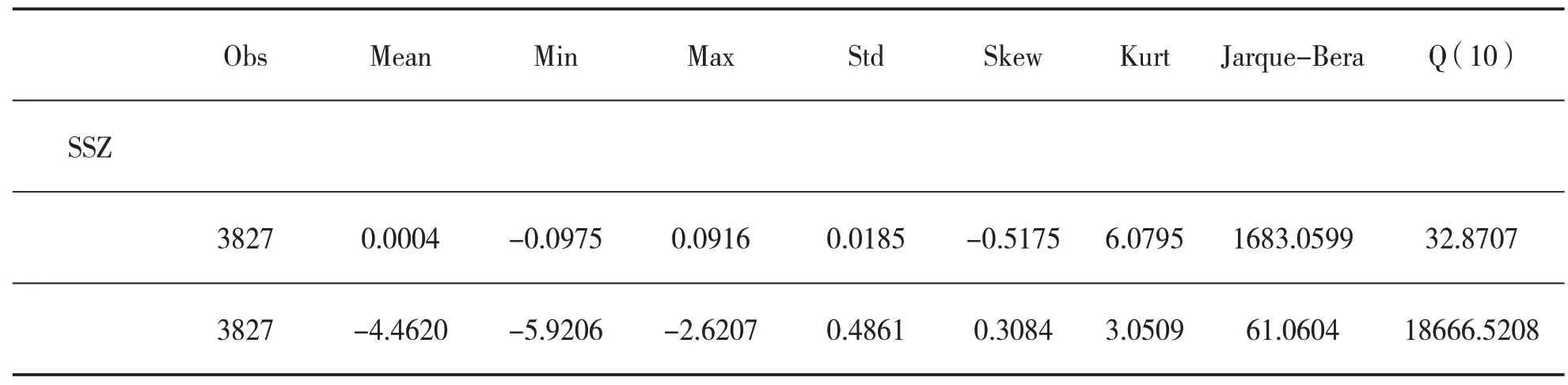
表1 指數日度資產收益率以及對數已實現測度描述性統計量

圖1 給出了上證綜合指數的日度指數資產收益率rt的QQ 圖.從上證綜合指數的日度指數資產收益率rt的QQ 圖可以看出，上證綜合指數的日度指數資產收益率rt不服從正態分布.這和Jarque-Bera 統計量得出的結論一致.

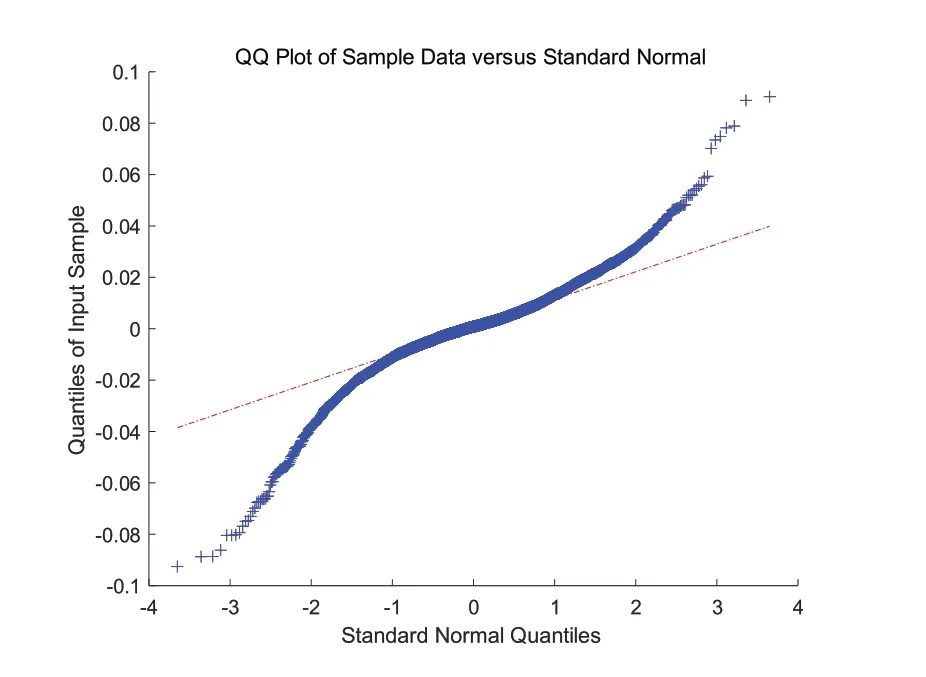
圖1 上證綜合指數的日度指數資產收益率rtQQ 圖

2.2 參數估計結果

運用極大似然方法得到TVP-RGAS 波動率模型以及RGAS 波動率模型的參數估計結果以及標準誤差、對數似然（Log-lik）和赤池信息準則（AIC）如表2所示.

由表2的結果可以看出，上證綜合指數中RGAS 波動率模型與TVP-RGAS 波動率模型中的杠桿系數τ1和τ2十分顯著，且τ1的估計值小于0，τ2的估計值大于0.說明國內股市存在明顯的杠桿效應（波動率的非對稱性）.上證綜合指數中參數A1，A2的值接近于1，說明波動率和自由度參數的持續性較強.上證綜合指數已實現方差的偏差調整系數ξ的估計值明顯小于零，表明上證綜合指數代表的股市已實現方差RV 是真實日度波動率的下偏估計，市場非交易時間效應強于微觀結構噪聲效應.從RGAS 估計出的υ的結果來看，上證綜合指數具有明顯的尖峰厚尾特征.因此，在對我國金融市場進行風險管理與控制時，需要充分考慮到收益率分布尖峰厚尾特征，從而更加有效度量市場風險.

表2 基于RGAS 波動率模型以及TVP-RGAS波動率模型參數的估計結果

比較RGAS 波動率模型的Log-lik 值和TVP-RGAS 波動率模型的AIC 值，可以判斷模型對數據的擬合效果，其中對數似然值越大、赤池信息準則值越小說明模型對數據的擬合效果越好；TVP-RGAS 波動率模型相較于RGAS 波動率模型擁有更大的對數似然值以及更小AIC值，說明TVP-RGAS 波動率模型對數據的擬合效果要優于RGAS 波動率模型.

圖2 給出了上證綜合指數的收益率序列圖、TVPRGAS 波動率模型對上證綜合指數的已實現方差RV 樣本內擬合圖以及自由度參數υ序列圖.由圖2 可以看出，上證綜合指數的收益率序列圖呈現出尖峰厚尾特征，上證綜合指數在抽樣階段內展現出明顯的波動率時變性和波動率聚集性特征.TVP-RGAS 波動率模型對上證綜合指數所代表的股票市場抽樣區間內的已實現方差RV擬合效果較好.

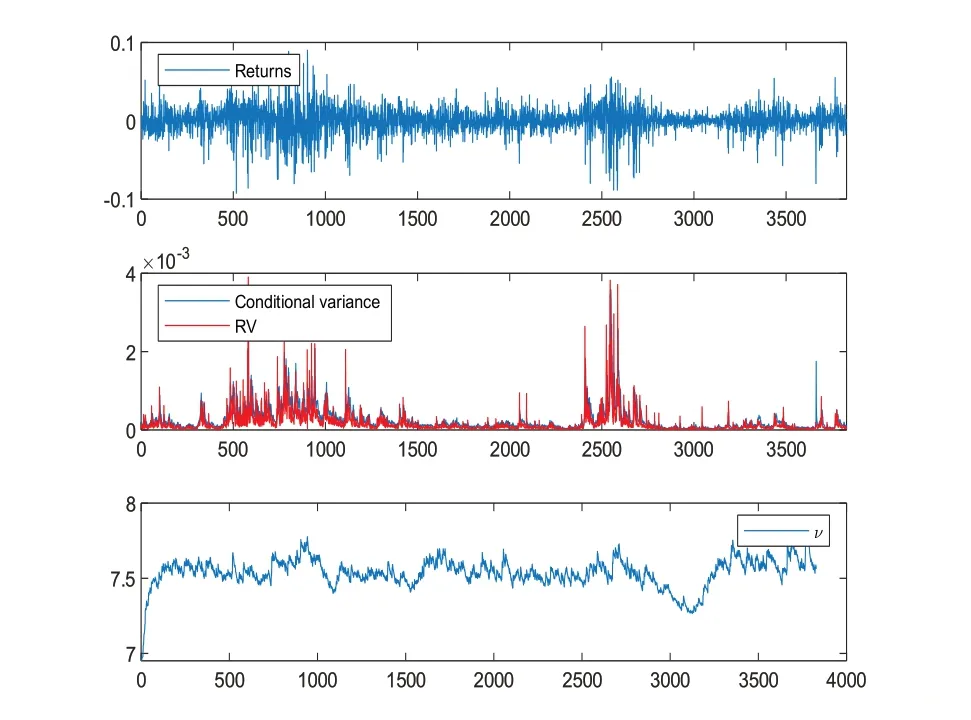
圖2 上證綜合指數日度收益率rt 序列圖、TVP-RGAS波動率模型對已實現方差RV的擬合圖以及自由度參數υ 序列圖

2.3 條件方差預測結果

為了考察TVP-RGAS 波動率模型的條件方差預測，本文采用RGARCH 模型、RGAS 波動率模型作為基準模型，比較TVP-RGAS 波動率模型和RGARCH 模型、RGAS波動率模型對條件方差預測精確性.為了能更好地比較TVP-RGAS 波動率模型以及RGARCH 模型對模型波動率預測精確性，選取均方根誤差（RMSE）、平均絕對誤差（MAE）以及均方誤差（MSE）以三個損失函數作為評價指標：

其中，RV是觀測的已實現方差，FV(m)是模型預測的波動率，m是波動率模型RGAS、TVP-RGAS 或RGARCH 模型.

表3 給出各模型波動率預測精確性評價結果，由表3可以看出相較于RGARCH 模型與RGAS 波動率模型，TVP-RGAS 波動率模型在三個損失函數評價指標下，均擁有最小的預測誤差，因此TVP-RGAS 波動率模型對數據的條件方差預測要強于RGARCH 模型以及RGAS 模型.在多數情況下RGAS 波動率模型的預測效果要優于RGARCH 模型，說明結合GAS 模型框架能夠在一定程度上提升模型對數據的預測效果.利用樣本內數據估計模型，基于估計結果可以獲得條件方差的預測值.在TVP-RGAS 波動率模型下，圖3 給出上證綜合指數基于TVP-RGAS 波動率模型得到的條件方差的預測結果.

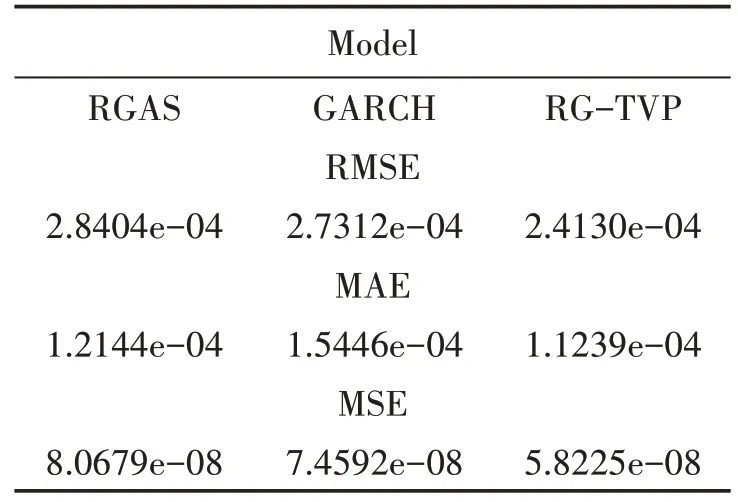
表3 上證綜合指數的波動率預測結果

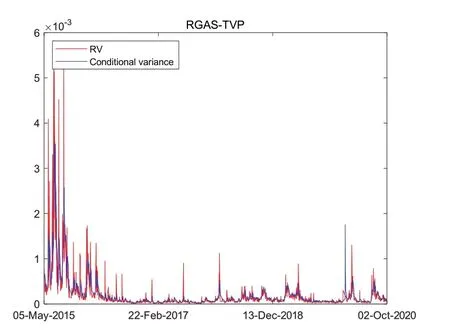
圖3 上證綜合指數指數條件方差預測結果

2.4 VaR 預測及后驗分析

準確測量金融市場風險對于金融機構的生存和發展乃至整個金融系統的穩定至關重要.VaR 是市場風險管理中最廣泛使用的工具，它因其概念簡單、直觀和易于計算等優點，成為許多風險管理者和金融機構計算市場風險的首選工具.下面基于TVP-RGAS 波動率模型的VaR 預測，討論后驗分析檢驗模型風險預測準確性.

VaR 是指在一定的置信度水平之下，某一金融資產或資產組合在未來特定時期的最大損失.t+1 時刻給定置信度水平1-α下的VaR定義為：

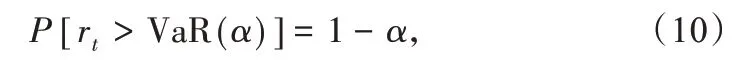
其中，P為概率，定義VaR 為負值，負號表示損失，rt≤VaR(α)定義為“失敗事件”.由上式可得TVP-RGAS 波動率模型的VaR的計算公式為：

其中，zα是資產收益率新息分布的α左尾分位數.實際上在TVP-RGAS波動率模型的假定下，zα是標準化t分布的分位數.

為了檢驗VaR 預測的準確性，我們采用了文獻中常用的后驗分析方法，即失敗率檢驗、Kupiec[37]引入的非條件覆蓋的似然比檢驗和Christoffersen[38]引入的條件覆蓋的似然比檢驗.非條件覆蓋的似然比檢驗的具體形式為：

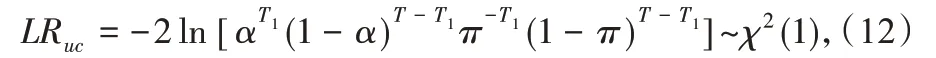
其中，T表示VaR 預測的總次數，T1表示“失敗事件”發生的次數，記為“失敗次數”，失敗率π=T1/T.非條件覆蓋的似然比檢驗LRuc不能保證“失敗事件”不受到前一次“失敗事件”的影響，因此Christoffersen[38]構建了獨立檢驗.該檢驗假設“失敗事件”發生與其上一次“失敗事件”發生是獨立的，假設成立時，似然函數比值LRind的形式為：

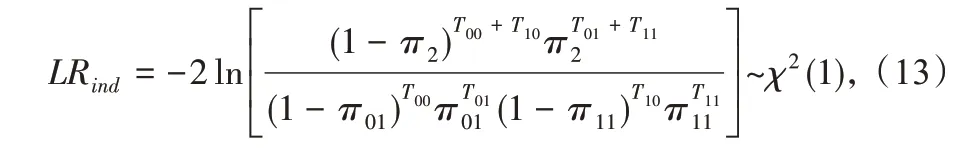
其中，π01=T01/(T00+T01)，π11=T11/(T10+T11)，π2=T01+T11/(T00+T01+T10+T11)，Tij表示兩次事件的發生，若i，j=0表示本次測度成功，即rt＞VaR(α)，i，j=1則表示本次測度失敗.Christoffersen[38]將非條件覆蓋的似然比檢驗與獨立檢驗相結合，建立了條件覆蓋的似然比檢驗LRcc，其形式如下：

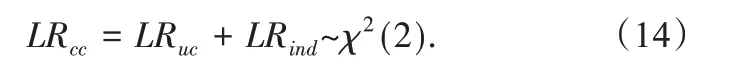
2.5 VaR預測及后驗分析結果

利用樣本內數據估計模型，基于估計結果可獲得條件方差的預測值.利用（10）式以及條件方差的預測值，可以得到上證綜合指數的VaR 結果.本文選取置信度水平為97.5%和95%（或顯著性概率水平2.5%和5%），得到TVPRGAS波動率模型下VaR預測結果如圖4所示.

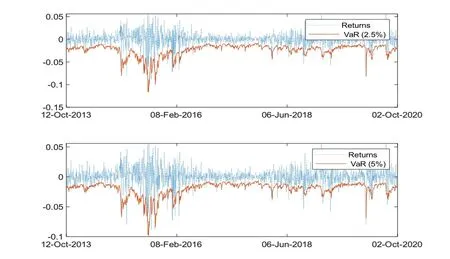
圖4 上證綜合指數VaR 預測結果

表4 給出了RGARCH 模型、RGAS 波動率模型與TVP-RGAS 波動率模型下的后驗分析結果，包括失敗率（FR）以及非條件覆蓋似然比統計量LRuc和條件覆蓋測試的似然比統計量LRcc.從表4 可以看出，TVP-RGAS 波動率模型的預測效果要優于RGAS 以及RGARCH 模型的VaR 預測效果.TVP-RGAS 波動率模型在α=0.025 和α=0.05 時通過了顯著性為5%的所有非條件覆蓋（LRuc）和條件覆蓋（LRcc）的似然比測試，而RGAS 波動率模型在α=0.025 時沒能通過非條件覆蓋（LRuc）和條件覆蓋（LRcc）的似然比測試，RGARCH 模型在α=0.05 時沒能通過非條件覆蓋（LRuc）和條件覆蓋（LRcc）的似然比測試.此外，TVP-RGAS 波動率模型總是擁有最接近顯著性概率水平的FR 值.由此可以看出，與RGAS 波動率模型相比，引入了高階矩特征的TVP-RGAS 波動率模型擁有更好的VaR 預測效果；與RGARCH 模型相比，可以描述厚尾分布的TVP-RGAS 波動率模型的VaR 預測更充分地利用了市場信息，更加合理地刻畫了資產收益率的尾部分布及波動性，從而改進了VaR 預測精確性.

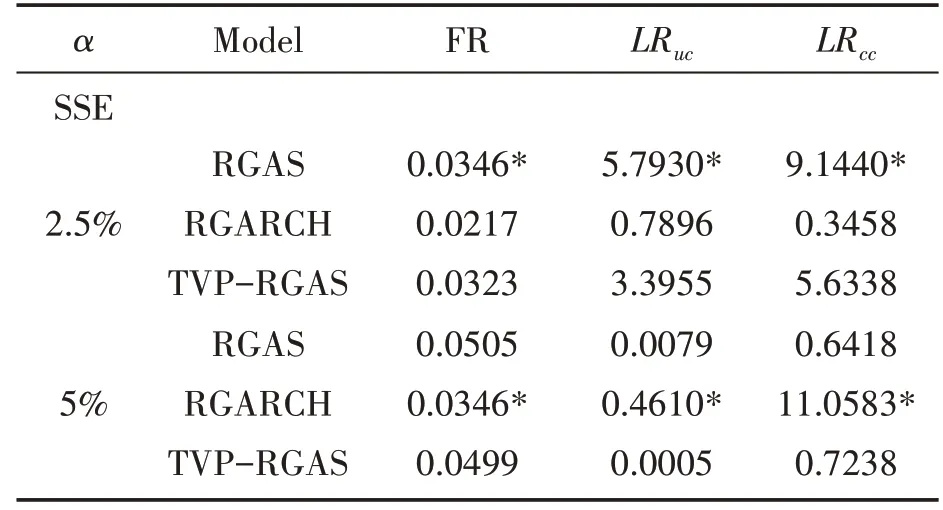
表4 上證綜合指數的VaR 預測的后驗分析

3 結語

本文基于傳統的GAS 模型框架，引入包含日內信息的已實現測度，假設資產收益率服從能夠捕獲尖峰厚尾特征的學生t分布，構建能夠捕獲時變高階矩信息的TVP-RGAS 波動率模型.采用上證綜合指數的5 分鐘高頻數據進行實證研究，得到以下研究結論：

（1）上證綜合指數日度指數收益率rt序列的偏度小于0，峰度大于3，呈現出左偏以及尖峰厚尾特征.同時Jarque-Bera 統計量顯著，說明日度指數收益率rt序列不服從正態分布.

（2）滬市已實現波動率的偏差修正參數ξ的估計值明顯小于0,表明已實現波動率是真實日度波動率的有偏估計,存在明顯下偏，滬市非交易時間效應強于微觀結構噪聲效應.

（3）根據極大似然值以及AIC 對模型進行比較分析，TVP-RGAS 波動率模型比RGAS 波動率模型擁有更好的數據擬合效果.

（4）根據三個損失函數得到的各模型波動率預測精確性評價結果，相較于RGAS 波動率模型以及RGARCH模型，TVP-RGAS 波動率模型總是擁有最小的計算誤差，即擁有更好的波動率預測效果.

（5）基于VaR的估計結果表明，相較于RGAS 波動率模型和RGARCH 模型，TVP-RGAS 波動率模型能夠更好地測量金融市場風險.

本文的研究工作為時變高階矩視角下對波動率建模提供了一種原理簡單且效果較好的方法，同時豐富了市場風險測量的實證結果.值得注意的是，本文的工作還有待進一步的擴展與完善，例如將能夠包含多種情況的偏斜廣義t分布（SGT）引入到TVP-RGAS 波動率模型中，在多個市場進行實證分析.當然，將模型運用在資產組合管理與衍生產品定價等問題中，也是切實可行的研究方向.