化整式為分式 證明整式不等式

江西省共青城市國科共青城實驗學校(332020) 姜坤崇

代數不等式從形式上大體可分為整式不等式、分式不等式及無理不等式等三類.整式不等式與分式不等式在證明中可以考慮互相轉化,文獻[1]闡述了將分式不等式轉化為整式不等式的重要作用,而轉化是相互的,因此對于某些整式不等式的證明,我們也可另辟蹊徑,將其轉化為分式不等式來證明,這種轉化經常會收到意想不到的證明效果,下面分類舉出數例說明之.

一、證明三元輪換對稱不等式

在一個含有三元a,b,c的不等式中,若同時將a換成b,b換成c,c換成a且不等式不發生改變,則稱這個不等式是關于a,b,c輪換對稱不等式.顯然,一個關于a,b,c對稱的不等式(任意對調其中的兩個字母不等式都不發生改變)的不等式一定是輪換對稱不等式,反之則不然.對于許多關于a,b,c輪換對稱的整式不等式化為分式不等式來證,可起到化繁為簡、化難為易的效果.

例1已知a,b,c ＞0, 求證:a3b+b3c+c3a≥abc(a+b+c).

分析這個整式不等式從表面上看不難,但保持整式的形式進行證明卻有一定困難,下面我們將其轉化為分式不等式來證明可化難為易.

證明原不等式可化為

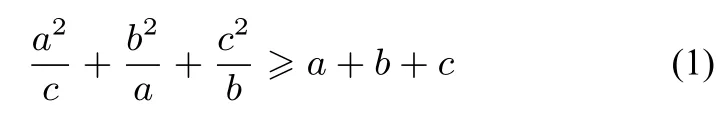
說明例1 也可以采用下面的方法來證明: 由7 元均值不等式得a3b+a3b+a3b+a3b+b3c+c3a+c3a≥= 7a2bc, 即4a3b+b3c+2c3a≥7a2bc, 同理,4b3c+c3a+2a3b≥7b2ca,4c3a+a3b+2b3c≥7c2ab,以上三個不等式相加得7(a3b+b3c+c3a)≥7(a2bc+ab2c+abc2),即a3b+b3c+c3a≥abc(a+b+c).

顯然,以上證明是不簡單也不易一下子想到的(為什么用7 元均值不等式? ),兩種證法比較,化為分式證明的方法要簡單得多.

有了對例1 解決問題方法的指引,以下例2、3、4、5 的解決就變得輕松多了.

例2(自編題)設a,b,c ＞0,求證:a3b2+b3c2+c3a2≥abc(ab+bc+ca).

證明將所證不等式化為分式不等式得

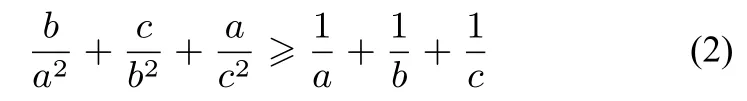
例3(自編題)設x,y,z是正實數,求證:x3y2(y+z)+y3z2(z+x)+z3x2(x+y)≥2xyz(xy2+yz2+zx2).

證明將所證不等式化為分式不等式得

例4(自編題)已知a,b,c ＞0,求證:a5b2+b5c2+c5a2≥a2b2c2(a+b+c).

證明原不等式可化為)

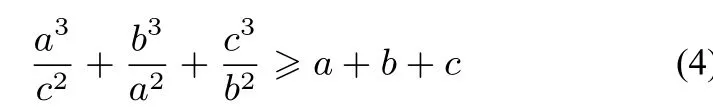
例5(自編題)已知a,b,c ＞0,求證:a8b3+b8c3+c8a3≥a3b3c3(a2+b2+c2).

證明原不等式可化為

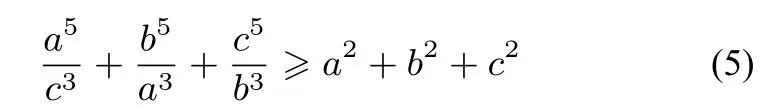
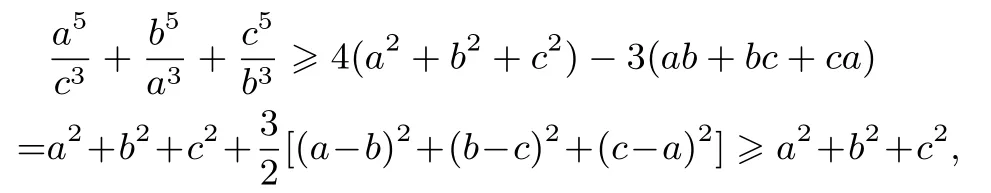
即(5)式成立,從而原不等式得證.

二、證明二元三元對稱不等式

例6已知x、y、z是正實數,求證:

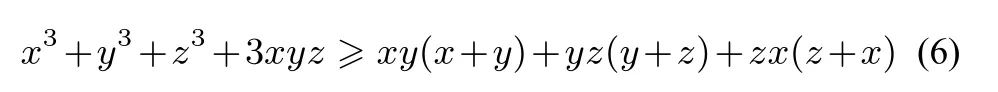
證明將不等式(6)等價轉化為一分式不等式得

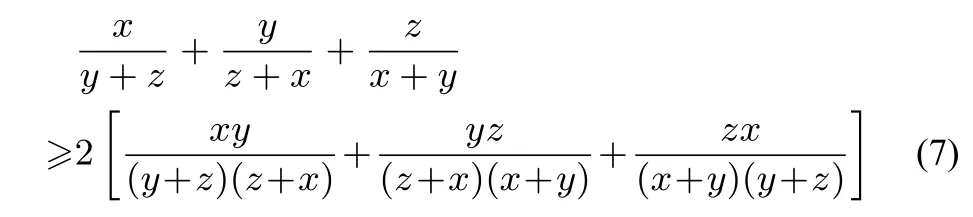
由二元均值不等式得

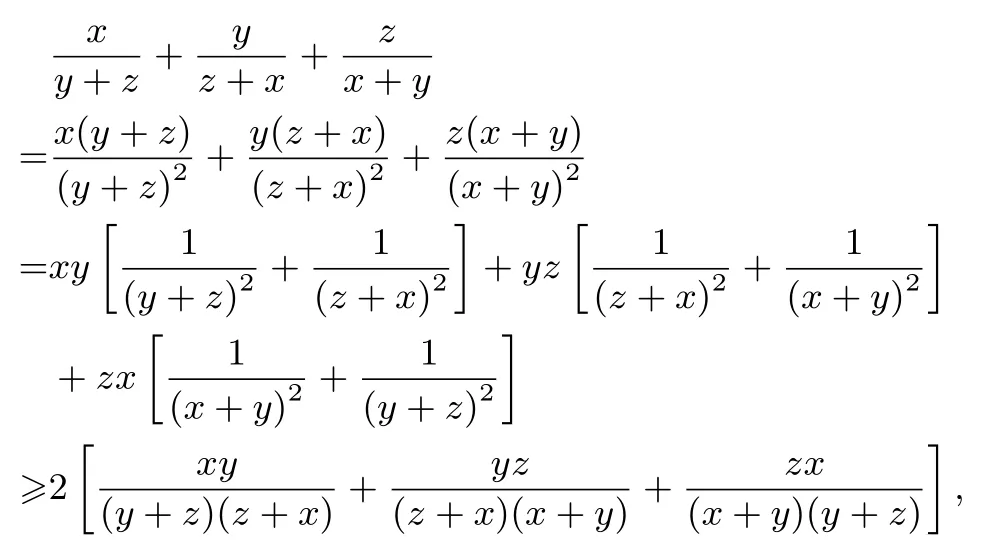
即(7)式成立,從而(6)式得證.

說明不等式(6)即著名的舒爾不等式:xr(x-y)(xz)+yr(y-z)(y-x)+zr(z-x)(z-y)≥0(其中x、y、z、r ＞0)當r= 1 時的一種等價形式,以上提供了一種證明舒爾不等式的新方法.

例7(自編題)設a,b,c ＞0, 求證:a2b2(a+b)4+b2c2(b+c)4+c2a2(c+a)4≥16a2b2c2(a2+b2+c2).

證明將不等式化為分式不等式得

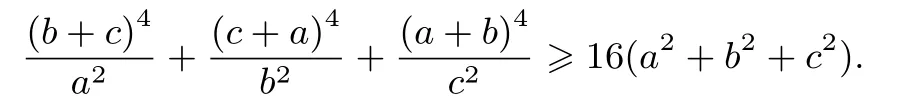
由三元均值不等式得

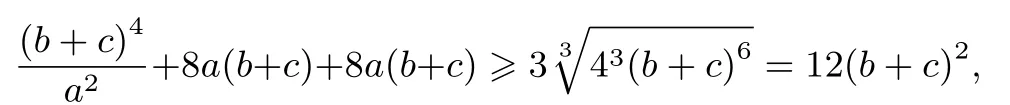
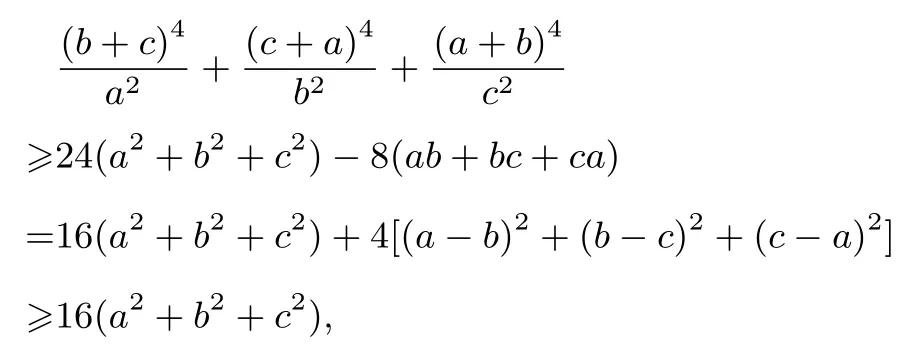
例8(自編題)設a ＞1,b ＞1,求證:a3+b3+8(a+b)≥a2+b2+8ab+8.

分析這個不等式直接證明不好證,而轉化為分式不等式證明則容易進行.

證明因為a ＞1,b ＞1,所以

由二元均值不等式得

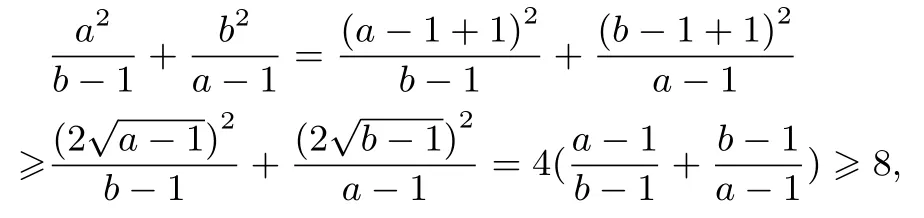
當且僅當a=b=2 時等號成立,所以原不等式成立.

說明不等式(8)為第26 屆獨聯體數學奧林匹克競賽題: 證明: 對任意a ＞1,b ＞1,有不等式≥8.

例9(自編題)設a ＞1,b ＞1,求證: 2(a4+b4)+27(a+b)≥2(a3+b3)+27ab+27.

證明因為a ＞1,b ＞1,所以

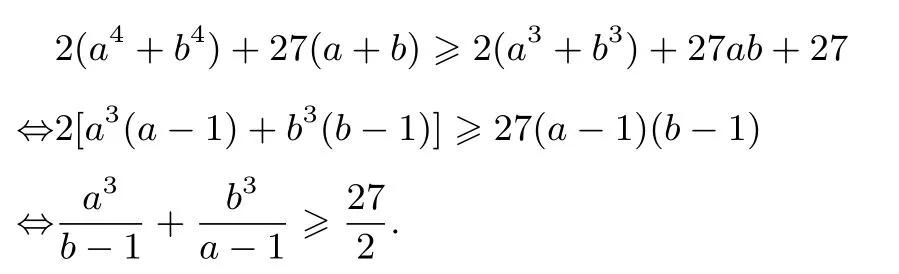
由二、三元均值不等式得

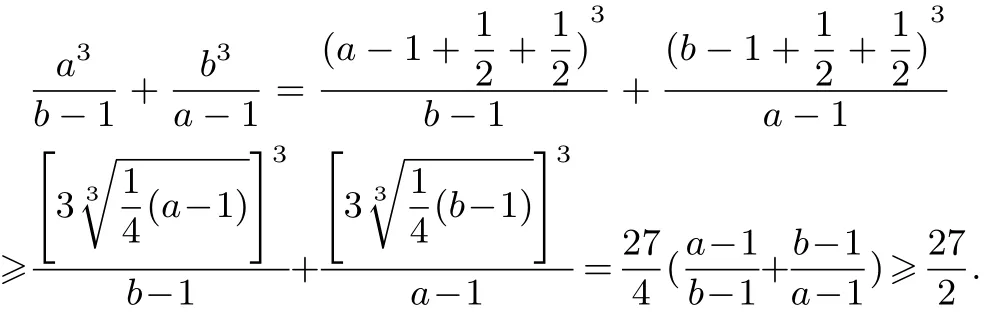
當且僅當a=b=時等號成立,所以原不等式成立.

例10(自 編 題)設a,b,c ＞0, 求證: (ab+bc+ca)[(a+b)2+(b+c)2+(c+a)2]≥12abc(a+b+c).

證明不等式可化為

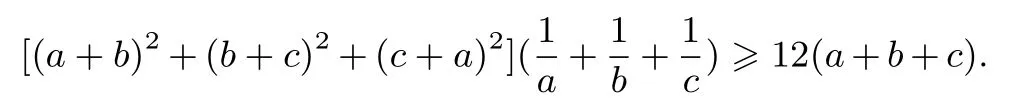
三、證明條件不等式

例11(自編題)已知實數a ＞1,b ＞1,c ＞1, 且a2+b2+c2=9,求證:a3+b3+c3≥

證明由a ＞1 得a-1＞0,a2-1＞0,由三元均值不等式得

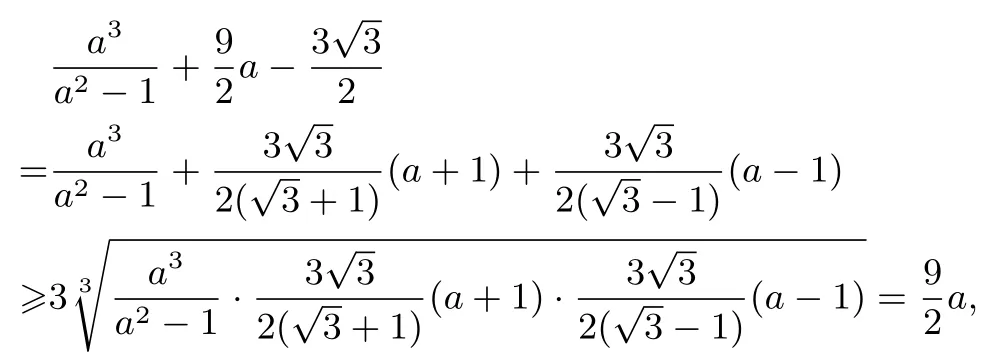
例12(自編題)已知實數a ＞1,b ＞1,c ＞1, 且a2+b2+c2=5,求證:a5+b5+c5≥

證明由a ＞1 得a-1＞0,a2-1＞0,由五元均值不等式得

當且僅當a=時上式等號成立.所以即同理,

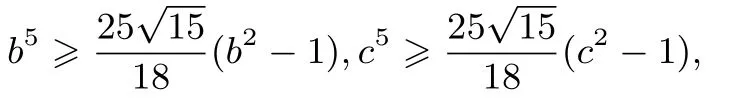
以上三式相加得

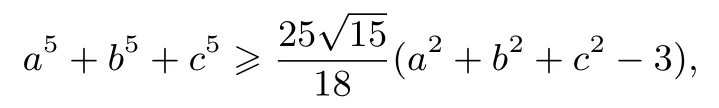
即a5+b5+c5≥

四、證明多元對稱不等式

例13(自編題)已知λ為正實數,xi ＞ λ(i=1,2,··· ,n,n≥3),k為整數,且k≥n,求證:

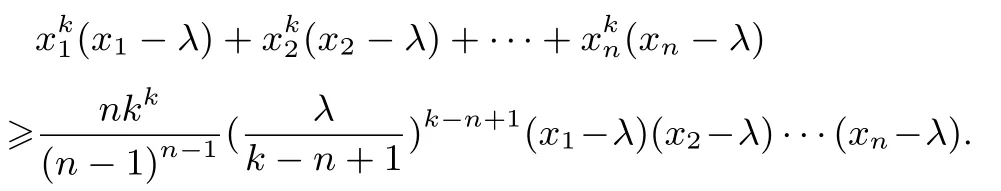
證明原不等式可化為

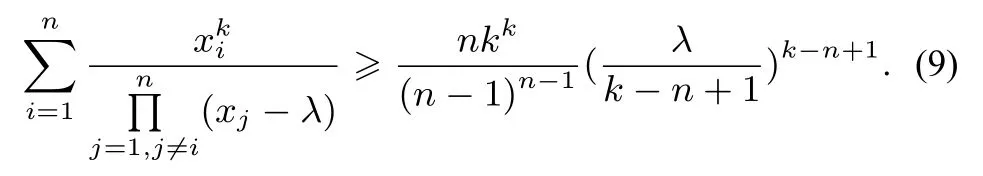
記Ai=

則由k元均值不等式得:

即

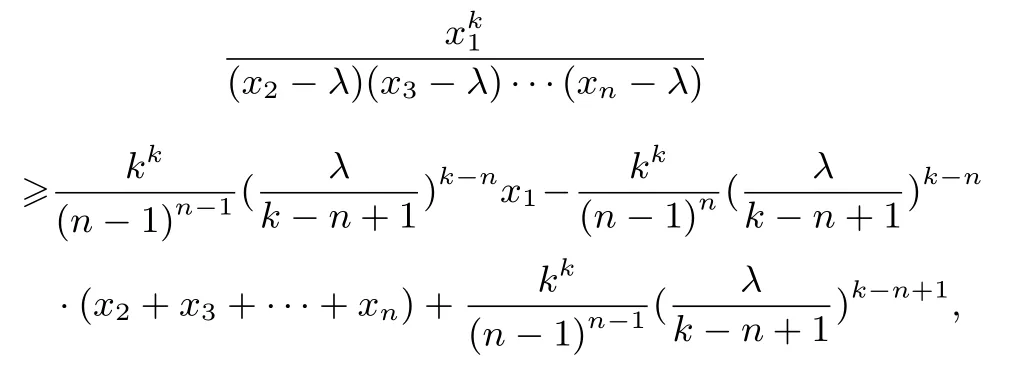
同理可證,

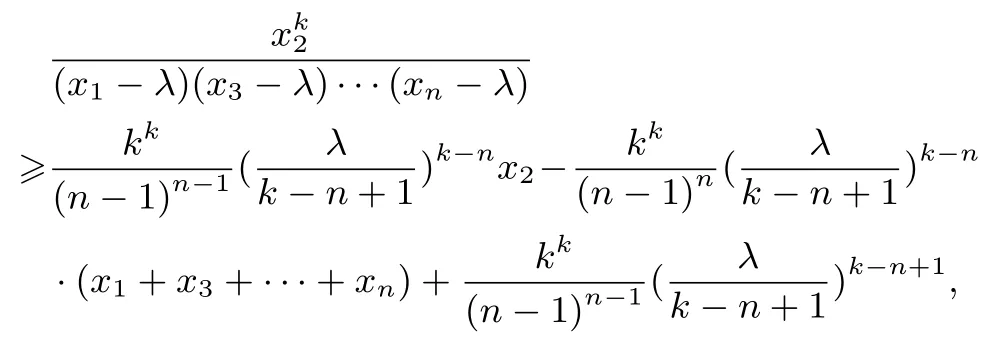
以上n個不等式相加即得不等式(9).

從以上的證明可以看出, 當且僅當xi=(i= 1,2,··· ,n)時所證不等式等號成立.所以原不等式成立.