探究Taylor公式視角下的偏移問題

華南師范大學數學科學學院(510631) 陳禧杰

一、極值點偏移和拐點偏移

極值點的定義大家是比較熟悉的, 即若f(x0)是函數f(x)的極大(小)值,則x0為函數f(x)的極大(小)值點,但拐點的定義可能不甚了解.

定義1[1]設f(x)在x0處連續.若曲線y=f(x)在(x0,f(x0))左右兩側的上下凹凸性相反,則稱(x0,f(x0))為曲線y=f(x)的拐點.

結合函數凹凸性的等價定義[1],可得:

性質1[1]: 若f(x)二階可導,有f′′(x0)= 0 且在x0兩側的二階導數異號,則(x0,f(x0))是曲線y=f(x)的拐點.

1.極值點偏移

定義2[2]已知函數y=f(x)在(a,b)上連續,且在區間(a,b)內只有一個極值點x0.對任意滿足f(x1)=f(x2)=m(m為常數), 且a ＜x1＜x0＜x2＜b的x1,x2,若都有x1+x2＞2x0,則稱函數f(x)在(a,b)上極值點x0左偏; 若都有x1+x2＜2x0, 則稱函數f(x)在(a,b)上極值點x0右偏.

極值點x0左偏的圖示可參看圖1.

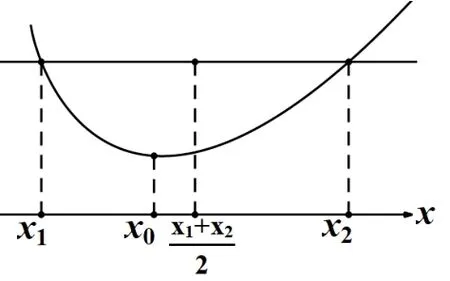
圖1

2.拐點偏移

在極值點偏移的基礎上,各地模擬題中又出現了拐點偏移,此類題型一般以某些函數在拐點兩側“凹凸程度”不同,導致函數圖像關于拐點不具有中心對稱性作為命題背景.下面給出拐點偏移的定義.

定義3[2]已知函數y=f(x)在(a,b)上連續,且在區間(a,b)內只有一個拐點x0.對任意滿足f(x1)+f(x2)= 2f(x0),且a ＜x1＜x0＜x2＜b的x1,x2, 若都有x1+x2＞2x0, 則稱函數f(x)在(a,b)上拐點x0左偏; 若都有x1+x2＜2x0, 則稱函數f(x)在(a,b)上拐點x0右偏.

拐點偏移的題目一般是針對f(x)是(a,b)上的單調函數而言的,以拐點左偏為例,見圖2.

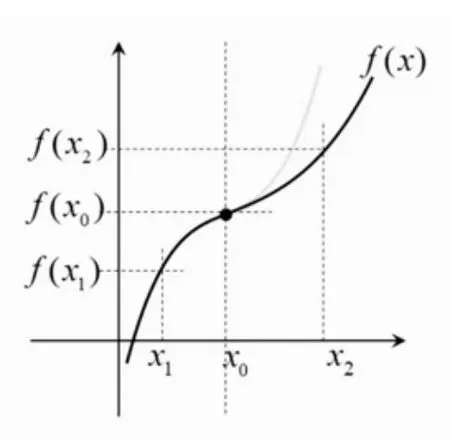
圖2

特別地,a可為-∞,b可為+∞.

二、Taylor 公式

高中階段經常會遇到含有ex和lnx的超越函數,若能用簡單的多項式函數來近似替代此類函數,而且誤差又能滿足要求,那么對函數值的近似計算具有重要意義,且在導數大題中可用于放縮來簡化不等式證明, 而在高等數學中的Taylor 公式便能達到這個效果.

定義4[1]若f(x)在x0的某鄰域U(x0)內有n+1 階導數,則對任意的x ∈U°(x0),存在ξ介于x和x0之間,使f(x)=Tn(x)+Rn(x),其中Tn(x)=(x-x0)k為f(x)在點x0處的n階Taylor 多項式,Rn(x)=(x-x0)n+1為Taylor 公式的Lagrange 型余項,其中ξ=x0+θ(x-x0)(0＜θ ＜1).(補充: 某鄰域U(x0)的含義是指以x0為中心,以某一常數r(r ＞0)作為半徑的一個開區間(x0-r,x0+r),U°(x0)=U(x0)/{x0})

中學階段可以直觀地理解為當n越大時,Tn(x)=(x-x0)k與函數f(x)的圖像就越相似.

三、Taylor 公式與偏移問題的聯系

事實上,極值點偏移與函數的軸對稱性有關,而拐點偏移則與函數的中心對稱性有關,可以分別對應中學階段熟悉的二次函數與三次函數.已知二次函數具有軸對稱性,其極值點恰為其對稱軸,而三次函數具有中心對稱性,其對稱中心恰為其拐點.所以在偏移問題上,按照定義2 和定義3 的背景,二次函數不發生極值點偏移,即=x0(x0為極值點); 三次函數不發生拐點偏移,即=f(x0)時有=x0(x0為拐點).然而,當f(x)在點x0處的二階Taylor 多項式T2(x)和三階Taylor 多項式T3(x)恰好分別為二次函數和三次函數,而且Taylor 多項式可以用于逼近原函數,所以可以嘗試通過分別對f(x)與T2(x)和f(x)與T3(x)的差異進行分析,將Taylor 公式與偏移問題聯系起來,下面來看看如何應用作差法分析其差異.

定理1[3]連續函數f(x)在(a,b)上有二階導數且只有一個極值點x0,f′(x)在(a,x0)和(x0,b)上異號,T2(x)=f(x0)+(x-x0)2為f(x)在x=x0處的二階Taylor多項式, 記差函數為D2(x)=f(x)- T2(x), 對任意滿足f(x1)=f(x2)=m(m為常數),且a ＜x1＜x0＜x2＜b的x1,x2:

(1)若D2(x)f′(x)＜0,?x /=x0,則x1+x2＞2x0,即函數f(x)在(a,b)上極值點x0左偏;

(2)若D2(x)f′(x)＞0,?x /=x0,則x1+x2＜2x0,即函數f(x)在(a,b)上極值點x0右偏.

證明[3]不妨設極值點x0為極小值點, 類似可證為極大值點的情況.因為二次函數T2(x)=f(x0)+(x-x0)2是以(x0,f(x0))為頂點, 以x=x0為對稱軸, 所以m ＞f(x0)時,T2(x)也必定存在兩個不等實根x′1,x′2使得f(x1)=f(x2)=m=T2(x′1)=T2(x′2),且由二次函數的軸對稱性可得x′1+x′2= 2x0, 故不妨設a ＜x′1＜x0＜x′2＜b.

(1)若D2(x)f′(x)＜0,?x /=x0,如圖3,因為x=x0為極小值點, 故x ∈(a,x0),f′(x)＜0, 所 以D2(x)=f(x)-T2(x)＞0,即f(x)＞T2(x).所以f(x′1)＞T2(x′1)=f(x1), 又因為f′(x)＜0,f(x)單調遞減, 所以可推出x′1＜x1.同理可證當x ＞x0時, 有x′2＜ x1.故由x′1＜ x1和x′2＜ x2可推出x1+x2＞x′1+x′2=2x0.

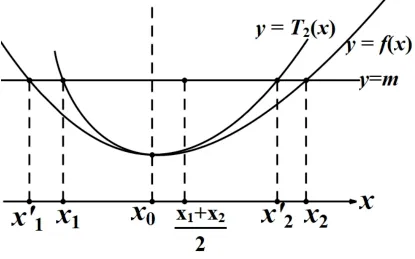
圖3

(2)若D2(x)f′(x)＞0,?x/=x0,同理可證得x1+x2＜x′1+x′2=2x0.

定理2連續的函數f(x)在(a,b)上有三階導數且 只 有一個拐點x0,f′′(x)在(a,x0)和(x0,b)上 異號,T3(x)=f(x0)+f′(x0)(x - x0)+(x-x0)3為f(x)在x=x0處的三階Taylor 多項式, 記差函數為D3(x)=f(x)-T3(x),對任意滿足f(x1)+f(x2)=2f(x0),且a ＜x1＜x0＜x2＜b的x1,x2:

(1)若f(x)單調遞增,當x ∈(a,x0)時,f′′(x)＜0(＞0)且D′3(x)＜0, 當x ∈(x0,b)時,f′′(x)＞0(＜0)且D′3(x)＞0,則x1+x2＜2x0,即拐點右偏;

(2)若f(x)單調遞增,當x ∈(a,x0)時,f′′(x)＜0(＞0)且D′3(x)＞0, 當x ∈(x0,b)時,f′′(x)＞0(＜0)且D′3(x)＜0,則x1+x2＞2x0,即拐點左偏;

(3)若f(x)單調遞減,當x ∈(a,x0)時,f′′(x)＜0(＞0)且D′3(x)＞0, 當x ∈(x0,b)時,f′′(x)＞0(＜0)且D′3(x)＜0,則x1+x2＜2x0,即拐點右偏;

(4)若f(x)單調遞減,當x ∈(a,x0)時,f′′(x)＜0(＞0)且D′3(x)＜0, 當x ∈(x0,b)時,f′′(x)＞0(＜0)且D′3(x)＞0,則x1+x2＞2x0,即拐點左偏.

證明不妨證“若f(x)單調遞增, 當x ∈(a,x0)時,f′′(x)＜0 且D′3(x)＜0, 當x ∈(x0,b)時,f′′(x)＞0 且D′3(x)＞0,則x1+x2＜2x0”,其他情況類似可證.

T3(x)=f(x0)+f′(x0)(x - x0)+(x-x0)3為f(x)在x=x0處的三階Taylor 多項式, 而T′3(x)=f′(x0)+(x-x0)2恰好等于f′(x)在x=x0處的二階Taylor 多項式, 而f′(x)代替f(x)后的D2(x)恰為D′3(x)=f′(x)-T′3(x).所以當x ∈(a,x0)時,f′′(x)＜0 且D′3(x)＜0,當x ∈(x0,b)時,f′′(x)＞0 且D′3(x)＞0,可推得D′3(x)f′′(x)＞0,?x /=x0,由定理1 可得f′(x)在(a,b)上極值點x0右偏.

令g(x)=f(x)+f(2x0-x),則g′(x)=f′(x)-f′(2x0-x).因為f′(x)在(a,b)上極值點x0右偏,所以對任意滿足f′(x1)=f′(x2),且a ＜x1＜x0＜x2＜b的x1,x2,若都有x1+x2＜2x0,則2x0-x1＞x2＞x0.因為當x ∈(x0,b)時,f′′(x)＞0, 所以f′(x)單調遞增, 得f′(2x0- x1)＞f′(x2)=f′(x1), 所以f′(x1)-f′(2x0-x1)＜0, 所以當x ∈(x0,b)時,g′(x)＜0, 所以g(x)在(a,x0)上單調遞減.同理可得,g(x)在(x0,b)上單調遞增.于是當x ∈(a,b)且x/=x0時,g(x)＞g(x0),即f(x)+f(2x0-x)＞2f(x0).所以f(2x0-x1)＞2f(x0)-f(x1)=f(x2).又因為f(x)在(a,b)單調遞增,所以2x0-x1＞x2,即x1+x2＜2x0.

四、實戰演練

經過上面的分析,我們從這兩個定理中得到了兩個用于證明偏移問題的判定定理,下面來嘗試應用到具體的例題當中.

例1(2016年高考全國卷Ⅰ理科第21 題)已知函數f(x)= (x-2)ex+a(x-1)2有兩個零點.(1)求a的取值范圍;(2)設x1,x2是f(x)的兩個零點,證明:x1+x2＜2.

解析(1)f′(x)= (x -1)(ex+ 2a), 分類討論后得a ∈(0,+∞),過程略.

(2)經分析得在R 上只存在一個極小值點x0= 1 且f(x1)=f(x2)= 0, 故不妨設x1＜1＜x2.f′′(x)=xex+ 2a得T2(x)=f(x0)+a)(x-1)2-e.D2(x)=f(x)-T2(x)=(x-2)ex+e.D′2(x)= (x-1)(ex -e), 易證在(-∞,1)和(1,+∞)上(ex -e)與(x-1)同號,所以D′2(x)≥0(當x= 1 時取等號),所以D2(x)是單調遞增的,故在(-∞,1)上D2(x)＜D2(1)= 0,在(1,+∞)上D2(x)＞D2(1)= 0.同時, 因為a ＞0,ex ＞0, 所以f′(x)= (x-1)(ex+2a)在(-∞,1)上f′(x)＜0, 在(1,+∞)上f′(x)＞0.綜上,D2(x)f′(x)＞0(?x/=1),所以由定理1 得x1+x2＜2x0=2.

例2([4] 中例2)設函數f(x)=xlnx -(1)求函數f(x)的單調區間; (2)證明: 當x1/=x2, 且f(x1)+f(x2)=0 時,x1+x2＞2.

解析(1)f(x)在(0,+∞)上單調遞減,過程略.

(2)令f′′(x)=-1=0,結合性質1 可分析得f(x)在(0,+∞)上只存在一個拐點x0= 1, 又f(x1)+f(x2)=0 = 2f(1), 故不妨設0＜ x1＜1＜ x2.T3(x)=f(x0)+f′(x0)(x-x0)+所以D′3(x)= (f(x)-T3(x))′= lnx+1-x+-1 + (x -1),+ 1.因為＞0, 所以在(0,+∞)上單調遞增, 又因為(1)= 0, 易得= 0, 所以D′3(x)在(0,+∞)上單調遞增, 又因為D′3(1)= 0, 所以當x ∈(0,1)時,f′′(x)=-1＞0 且D′3(x)＜0, 當x ∈(1,+∞)時,f′′(x)＜0 且D′3(x)＞0,所以由定理2 可得x1+x2＞2x0=2.

五、總結

本文通過結合Taylor 公式和二次函數的軸對稱性和三次函數的中心對稱性找到解決“極值點偏移”和“拐點偏移”問題的兩條判定定理,將兩類偏移問題通過Taylor 公式統一起來.所以在平時的學習中,若能對這類有明顯特征的題目進行問題本源的探究,得出一般化的解題策略,便能做到“四兩撥千斤”,避免題海戰術,提升思維的廣闊性.