(T700/環氧)/EPDM粘接界面參數的實驗測試及反演分析

趙朝坤，劉應雷，劉 凱，魏 超

(1.中國航天科技集團有限公司第四研究院，西安 710025；2.中國航天科技集團有限公司四院四十一所，西安 710025)

0 引言

近年來，隨著輕質高承載纖維材料的廣泛應用以及異型連續纏繞工藝的不斷成熟，“飛馬座”采用的“纏繞固定+彈性緩沖”復合吊耳結構應用前景廣泛。“飛馬座”吊耳結構存在纖維殼體/橡膠層粘接界面，粘接界面是最容易發生失效的區域之一，確定粘接界面參數對進行吊耳結構設計具有重要意義。

粘接界面力學特性的表征一直是難點和熱點，國內外學者對粘接界面進行了大量實驗研究。韋震、周清春等[1-5]采用拉伸實驗研究了固體火箭發動機中粘接界面的宏觀力學性能。劉龍權等[6]通過單搭接剪切實驗測定了金屬-復合材料粘接界面參數。ANDERSONS等[7]通過實驗研究了復合材料分層擴展方向對斷裂韌性的影響。REEDER[8]總結了幾種不同復合材料粘接界面Ⅰ型和Ⅱ型斷裂韌性與斷裂韌性之間的比值關系。BALZANI等[9]采用雙懸臂梁模型和復合型斷裂彎曲模型測定了單向纖維增強復合材料的層間界面參數。SILVA等[10]研究了粘接結構中界面斷裂韌性對結構整體強度的影響。SONG M G等[11]通過實驗研究了制備工藝、被粘材料厚度等因素對由復合材料板單搭接接頭剪切性能的影響。SORENSEN等[12]采用四點彎曲實驗對玻璃纖維增強復合材料的分層情況和整體強度規律進行了研究。CLAY等[13]通過實驗測定了金屬-復合材料粘接界面的力學性能參數。

完成粘接界面力學實驗后，基于實驗結果的參數反演識別是表征粘接界面力學特性的關鍵。VOREL等[14]基于順序線性分析(sequentially linear analysis)理論，提出了一種識別粘接界面牽引-分離關系的數值方法，該方法表現出優異的數值穩定性和通用性。AIROLDI[15]等采用梯度優化算法，確定了雙線性內聚力模型的本構參數。VALOROSO等[16]采用單純形法和梯度置信區間法，識別了指數內聚力模型的界面參數。ZHAO Haifeng 等[17]采用神經網絡提取了金屬薄膜/陶瓷界面的界面強度和斷裂韌性。WANG J等[18]結合雙懸臂梁試驗數據、數值仿真結果和遺傳算法，確定了率相關內聚力模型的界面參數。XU Y等[19]提出了通過多種實驗數據信息識別粘接層界面參數的組合式反演優化算法。劉偉先等[20]采用遺傳算法，對復合材料帶孔層合板的損傷參數進行了反演識別。林雪慧[21]將梯度優化方法、人工神經網絡方法和遺傳算法分別引入雜交反演過程中，提取了多相復合材料的非規則界面參數。王娟[22]發展了一種基于實驗的一體化反演識別方法。靳國輝[23]基于分步優化法和能量法，提出了一種指數型內聚力模型界面參數的反演方法。陳雄等[24]通過直接搜索算法，對HTPB推進劑與襯層粘接界面的力學性能參數進行了反演分析。韓龍等[25]基于Hooke-Jeeves算法，對HTPB/IPDI復合固體推進劑細觀界面參數進行了反演分析。封濤等[26]提出了一種考慮顆粒粒徑影響的分布反演優化算法。

本文首先設計了DCSB試件的I型分層擴展實驗，結合有限元仿真分析結果，確定了(T700/環氧)/EPDM粘接界面參數的初始值,并以其為基準，基于廣義回歸神經網絡(GRNN)對(T700/環氧)/EPDM粘接界面參數的準確值進行反演分析，為固體發動機關鍵復合材料界面特性研究與界面質量控制技術提供參考。

1 DCSB試件的Ⅰ型分層擴展實驗

參考周清春和賈登等[3-4]的實驗方案，為提高裂紋尖端附近應力沿寬度方向的均勻性，對試件寬度B進行優化，設計了圖1所示的DCSB試件，表1列出了試件的主要尺寸。

采用T700/環氧復合材料板材，經切割等工序按表1中的尺寸制件，經高溫模壓制成試件。為預制裂紋、保證剝離位置，在T700/環氧復合材料與EPDM之間放置0.1 mm厚的聚四氟乙烯片預制裂紋，預制裂紋長度a0=30 mm。為提高整個試件的剛度，并保護復合材料表面不受破壞，在復合材料版兩側粘接鋼質梁臂；(T700/環氧)/鋼界面還具備一定的剛度，在加載過程中，該界面的彈性變形相對較小，以不至于給實驗引入系統誤差。

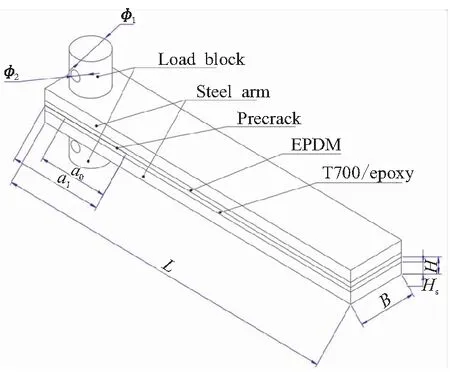
圖1 雙懸臂夾層梁(DCSB)試件

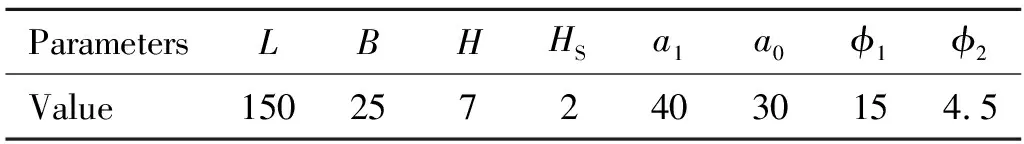
表1 DCSB試件尺寸

將表觀無缺陷、無膠團的3組DCSB試件編號為1、2、3，在INSTRON5982萬能材料試驗機上分別對其進行Ⅰ型分層擴展實驗。試件采用銷釘通過夾持孔與試驗機上下接頭鉸接，未加載端不受約束，在室溫(21 ℃)以5 mm/min的恒定位移加載速率拉伸DCSB試件，獲得的3組載荷-位移曲線如圖2所示。

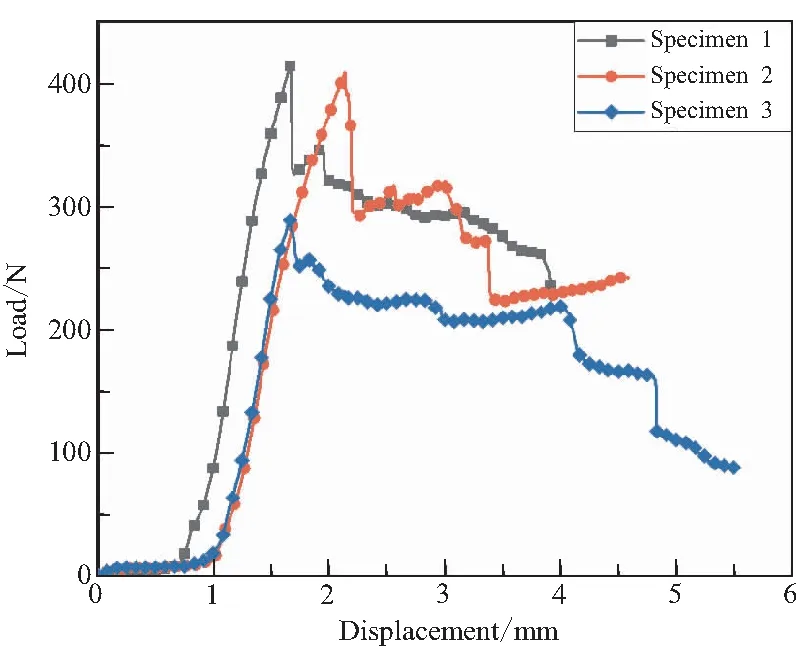
圖2 DCSB試件Ⅰ型分層擴展實驗的載荷-位移曲線

3號試件因制作過程中的工藝波動導致界面粘接不完全，后期進行了灌膠，實驗得到的載荷-位移曲線峰值較低，整體規律與1號、2號不一致。考慮到實際產品通常粘接界面良好，無界面脫粘現象，因此本文只研究完全粘接的界面，在后續處理實驗數據過程中舍棄3號實驗據。

根據材料力學中的懸臂梁理論，加載點載荷F與加載點位移w具有如下關系：

(1)

式中E為懸臂梁的彈性模量；B為試件寬度；H為試件的半高；a為裂紋長度。

式(1)表明，加載點載荷與位移在加載初期成線性關系，在后續處理實驗數據的過程中，對初始階段進行線性處理，且將起點平移至原點。

2 粘接界面參數反演分析初始值的確定

線彈性斷裂力學中，計算粘接界面的斷裂韌性的Irwin-Kies公式為[27]

(2)

式中Fmax為臨界載荷(峰值載荷)；a0為預制裂紋長度。

式(2)假定被粘接結構為各向同性材料且僅發生小變形，EPDM材料在(T700/環氧)/EPDM粘接試件裂紋擴展過程中存在大變形，同時T700/環氧復合材料為各向異性，采用該公式計算界面參數存在一定誤差。本文僅用式(2)的計算結果作為有限元仿真的(T700/環氧)/EPDM粘接界面參數初始值，通過有限元仿真進一步確定參數反演的初始值，不影響最終反演分析結果。根據實驗結果，采用式(2)計算(T700/環氧)/EPDM粘接界面的斷裂韌性，如表2所示。

表2 DCSB實驗的載荷峰值及式(2)確定的斷裂韌性

在初步確定GIc后，可在一定范圍內假設界面參數σmax，0對DCSB試件進行有限元計算，使計算的載荷-位移曲線與實驗曲線匹配，從而獲得確定σmax，0的初始值。

采用表1中的尺寸參數，在ABAQUS中建立了DCSB試件的二維有限元模型，裂紋尖端的網格如圖3所示。鋼質梁臂采用四邊形主導的自由網格，最大尺寸為1 mm，最小尺寸為0.1 mm，兩側邊設置Single形式的種子分布，單元類型為CPE4和CPE3；T700/環氧復合材料層采用四邊形結構化網格，網格尺寸為0.1 mm，單元類型為CPE4；EPDM采用四邊形結構化網格且網格尺寸為0.1 mm，單元類型為CPE4H；膠層厚度設置為0.1 mm，采用四邊形掃略網格，其單元類型設置為文獻[28]中用戶自定義的界面單元，單元尺寸為0.1 mm×0.1 mm。

圖3 DCSB試件裂紋尖端的有限元模型

鋼的彈性模量為210 GPa，泊松比為0.3；為簡化計算，T700/環氧復合材料的彈性模量為80 GPa，泊松比為0.25；EPDM的Yeoh超彈本構參數為C10=0.383 MPa、C20=-1.665×10-3MPa、C30=5.753×10-6MPa。載荷及邊界條件與DCSB試件的I型分層擴展實驗一致。將界面斷裂韌性 設置初步確定的值0.137 N/mm，法向初始強度 依次設置為0.1、1、10、100 MPa進行計算，計算結果如圖4所示。

圖4中，當σmax,0逐漸增大時，載荷-位移曲線的峰值增大，初始段曲線的斜率增大，最大載荷點向左上方移動。σmax,0=10 MPa時，計算的載荷位移曲線與實驗曲線的形狀較為接近，但峰值點的位移與實驗相差較大；σmax,0=1 MPa時，計算的載荷位移曲線與實驗曲線初始段的斜率較為接近。當σmax,0=1 MPa時，GIc分別為0.137、0.3、0.5、0.7、0.9 N/mm時，DCSB試件加載點的載荷-位移曲線如圖5所示。

圖4 GIc=0.137 N/mm時不同σmax,0計算的載荷-位移曲線

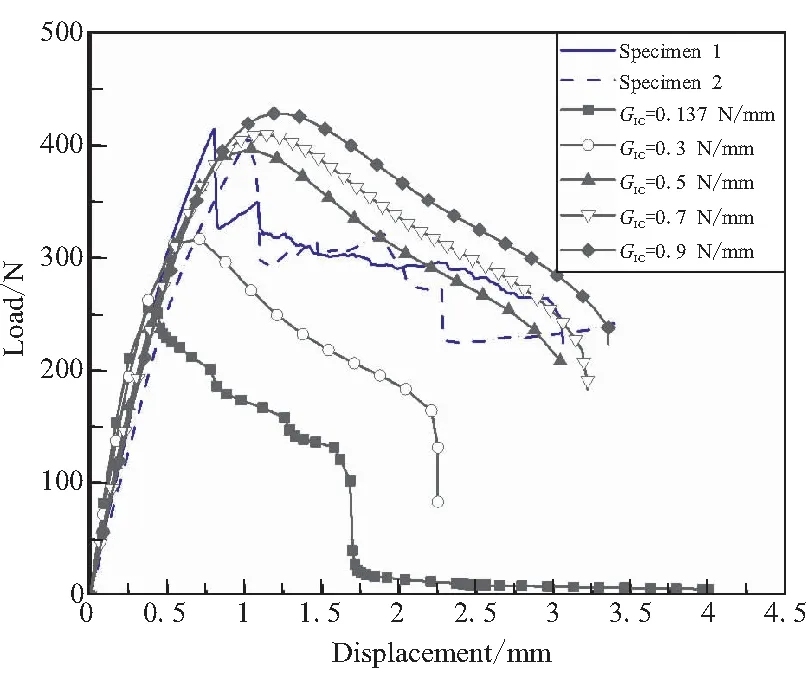
圖5 σmax,0=1 MPa時不同GIc計算的載荷-位移曲線

圖5中，當GIc逐漸增大時，載荷-位移曲線的峰值增大，初始段曲線的斜率變化較小，最大載荷點向右上方移動；當GIc=0.5 N/mm時，計算的載荷-位移曲線的與實驗曲線的形狀及峰值點坐標較為接近。經過上述擬合計算，確定了(T700/環氧)/EPDM粘接層界面反演分析參數的初始值為GIc=0.5 N/mm、σmax,0=1.0 MPa。

3 基于GRNN的界面參數反演

以第2章擬合的界面參數為基準，經完全交叉分組的析因設計及對應的有限元分析(FEA)結果構造了FEA輸出-界面參數的數據樣本，采用廣義回歸神經網絡(GRNN)對(T700/環氧)/EPDM粘接界面參數的準確值進行反演識別。

3.1 參數反演的基本原理

GRNN中，與輸入向量X對應的輸出向量估計值為

(3)

式中n為訓練樣本的數量；Xi、Yi分別為第i個訓練樣本的輸入和輸出；k為平滑參數。

根據式(3)可構造GRNN神經網絡結構。GRNN網絡的訓練過程中，需不斷調整平滑參數k以獲得最佳回歸估計結果，最優平滑參數與最小誤差序列均方值E相對應，具體詳見參考文獻[29]。

3.2 粘接界面參數反演

為獲得建立GRNN所需的訓練樣本，將表2中(T700/環氧)/EPDM粘接層界面參數的初始值進行拉偏處理。將σmax,0的值取為0.75、1、1.25、1.5、1.75 MPa，GIc的值依次取為0.4、0.45、0.5、0.55、0.6 N/mm，并進行完全交叉分組計算，可獲得25組加載點的載荷-位移曲線。當DCSB試件(T700/環氧)/EPDM粘接層的界面裂紋發生不穩定擴展后，由于試件橡膠層存在大變形，載荷-位移曲線出現較大的波動，規律性較差。因此，僅采用實驗載荷-位移曲線的上升段對GIc和σmax,0進行反演識別。訓練過程中，kmin1=5.60、kmax1=22、，kmin2=7.28、kmax2=40，1號實驗和2號實驗的誤差序列均方值相對于平滑參數的變化曲線如圖6所示，與最小的誤差序列均方值對應的最優平滑參數k1=12.73、k2= 21.16。

將25組載荷向量及對應的界面參數作為訓練樣本，平滑參數分別設置為k1=12.73和k2=21.16對GRNN進行訓練，將實驗的載荷向量作為輸入，反演得到(T700/環氧)/EPDM粘接層的界面參數如表3所示。將表3中的界面參數分別代入DCSB中的有限元模型進行計算，得到加載點的載荷-位移曲線與實驗曲線的結果如圖7所示。圖7中，與采用界面反演參數初始值(GIc=0.5 N/mm、σmax,0=1.0 MPa)仿真結果相比，采用1號和2號實驗數據反演的界面參數(見表3)，計算獲得的載荷-位移曲線與實驗結果吻合更好。1號實驗和2號實驗的反演結果中，2號實驗反演的參數計算的載荷-位移曲線與2號實驗結果重合較好，但與1號實驗的偏離稍微較大；而1號實驗反演的參數計算的載荷-位移曲線介于1號和2號實驗曲線之間，峰值載荷為411.27 N，與1號實驗和2號實驗的載荷峰值411.36 N的差值的平均值只有2.72 N，而通過實驗擬合結果計算的峰值點差值的均值達到了41.36 N。因此，通過GRNN的反演，最終確定(T700/環氧)/EPDM粘接層的界面參數為斷裂韌性GIc=0.575 N/mm、法向初始強度σmax,0=1.25 MPa。

(a)No.1 test (b)No.2 test

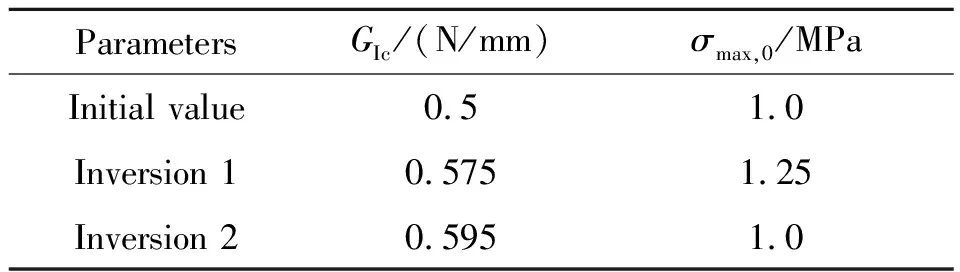
表3 反演的(T700/環氧)/EPDM粘接層界面參數

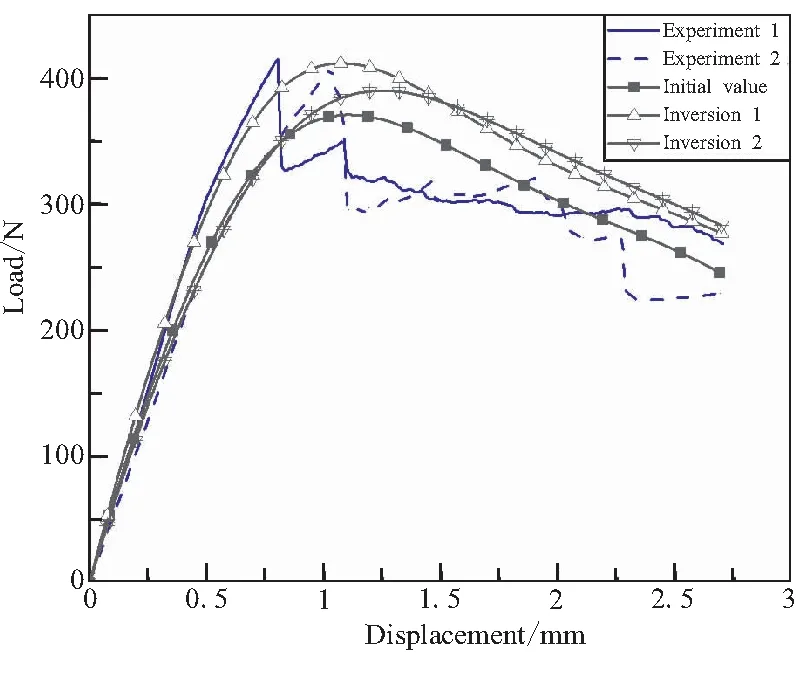
圖7 加載點載荷-位移曲線的對比結果

4 結論

(1)(T700/環氧)/EPDM粘接界面法向初始強度的改變對雙懸臂夾層梁I型分層擴展實驗加載點載荷-位移曲線峰值和初始段斜率均會產生較大影響；斷裂韌性的改變對峰值有較大影響，對初始段的斜率影響較小。

(2)在雙懸臂夾層梁Ⅰ型分層擴展實驗與有限元仿真分析的基礎上，采用廣義回歸神經網絡反演獲得(T700/環氧)/EPDM粘接界面的斷裂韌性GIc=0.575 N/mm，法向初始強度σmax,0=1.25 MPa；反演結果與實驗結果對比分析表明，結合DCSB I型分層擴展實驗、有限元仿真分析和廣義回歸神經網絡，可確定(T700/環氧)/EPDM粘接界面參數的準確值。