打破“局部”思維，提高“整體”意識

陳融敏

【摘要】學生在思考和解決問題時，往往習慣于從問題的局部出發，執著于從某個條件進行突破，而忽視題目的整體結構，從而導致解題過程繁瑣、運算量大，最后無功而返。教師在數學教學中應注意適時地滲透“整體思想”，幫學生打破“局部”思維，提高學生的“整體”意識和解決實際問題的能力。

【關鍵詞】整體思想;局部思維;教學滲透;解決問題

“整體思想”作為現代數學中一種十分重要的數學思想方法，對今后的數學學習，能力培養，思維啟發都有著不可代替的作用，因此在小學數學中滲透“整體思想”是十分有必要的。下面就以人教版小學數學的幾個具體例子來談談如何滲透“整體思想”，打破“局部思維”。

一、去“繁瑣”，破“局部”

在解決問題過程中，學生經常會有“只見樹木，不見森林”的局部思維，經常思路被問題中的某個條件牽著鼻子走，導致按照常規的方法和步驟不但不能直接得到結果，還會使解題過程變得十分繁瑣。那么這個時候就需要教師適時的引導，在關鍵的時刻幫助學生打破“局部”限制，發現“整體”，從而找到解題的捷徑。下面舉一道題為例子：

案例1：A、B兩地相距100千米，甲、乙兩人同時從兩地出發，相向而行。甲每小時走4千米，乙每小時走6千米。乙帶了一條狗，狗與乙同時出發，狗每小時跑10千米。當狗碰到甲的時候，狗立即掉頭往回跑，當狗碰到乙后又立即掉頭往回跑，狗就這樣在甲乙兩人之間往返跑，直到甲乙兩人相遇為止，問題是：這只狗一共跑了多少千米的路？

分析：當看到這道題，很多學生的思維馬上就會被來回不斷跑的狗牽走了，思維差一點的學生第一反應可能就往這條狗到底來回跑了幾趟這個方向去想，結果就是毫無頭緒。思維好一點的學生有能力計算第一次狗與甲相遇的時間，進一步算出此時狗跑了多遠;再算出此時狗與乙的距離，再接著算出狗第一次往回跑與乙相遇的時間，進一步算出狗跑了多遠......但是這樣算下去，越往后面算就越繁雜，會讓人感到沒有盡頭，陷入“無限”的循環中。

當學生的思路跟著狗跑的時候，就已經上當了。他們執著于求出狗到底跑了多少個來回，每個來回又分別跑了多遠，硬生生把自己的思路禁錮在這個“無限的循環中”。這也是常規思維惹的禍，當常規的方法步驟遇上稍微靈活的題目時，學生就容易產生思維的局部禁錮，從而看不到整體。

而此時教師稍加引導，提問：“如何求路程，路程等于什么？”

生：路程=速度×時間。

而題目已知狗奔跑的速度，就差狗奔跑的時間，而狗奔跑的時間一定要從狗身上入手嗎？

教師再追問：“狗奔跑的時間和誰的時間是一樣的”

生：狗奔跑的時間與甲乙兩人相遇時的時間是一樣的。

師：“那么甲乙兩人相遇的時間能不能求呢？”

這時候大部分的學生都恍然大悟，因為他們已經意識到問題的突破口在哪里了。甲、乙兩人從出發到相遇，所需時間是：100÷（6+4）=10（小時），所以狗奔跑的時間也是10個小時。又因為狗跑的路程=狗的速度×狗跑的時間，即：10×10=100千米，最后學生發現這道題跟狗到底跑了幾個來回根本沒有關系，當跳出“局部”，發現“整體”的時候，你會發現，簡直妙不可言。

二、棄“零散”，觀“全局”

在解決幾何圖形問題中，經常會有添加輔助線以助解題的方法，而“整體思想”也經常能被應用在解決集合圖形的問題上，下面我們一起來看一道習題。

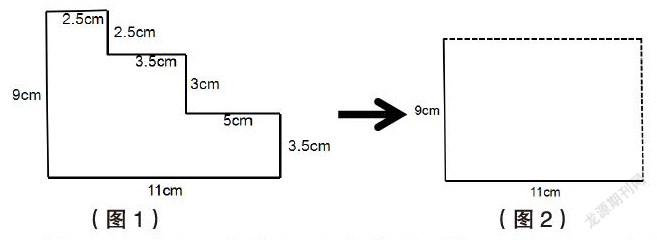
案例2：如圖，求出圖1的周長？

分析：當看到這道題時，大部分學生第一反應就是根據周長的定義，將圍成圖形的每一條邊都加起來，這樣就能求出這個圖形的周長。顯然，此時學生的思考限于局部，只看到了零散的幾條邊，無端的走上了復雜，運算量大的解題之路。

此時教師及時引導學生思考：能不能將零散的幾條邊進行重組，使這個不規則的圖形變成規則的圖形？

有些學生瞬間就恍然大悟，只要將三條豎邊平移到最右邊，將三條橫邊平移到最上面，圖1就轉化成了圖2的長方形，此時雖然圖形的形狀改變了，但是圖形的周長卻沒有改變。這時候再來求圖形的周長就非常簡單了。

三、尋“本質”，看“整體”

在解決問題過程中，整體意識薄弱的學生經常會被眼前細小、局部的條件所蒙蔽，看不到數學的本質和整體。筆者在六年級的教學過程中，發現有這樣一道題，題目中的條件經常能迷惑學生，讓他們無從下手。下面我們一起來看這道題：

案例3：如圖，圓內有一個直角三角形，兩條直角邊都

是圓的半徑，三角形的面積是4平方厘米，那么這個圓的

面積是多少平方厘米？

分析：因為圓的面積= ，所以要求圓的面積，只需要求出圓的半徑即可。根據題目所給條件，學生容易得出三角形的面積=r×r÷2=4，進而得出 。

在這里，半徑是多少就成了遮住學生眼睛的那片葉子，學生執著于常規方法，一定要求出半徑r是多少，才能去求圓的面積。他們沒想到如果將 看成一個整體，直接代入到圓的面積公式中，即可得到圓的面積= 。

從上面的幾個案例可以看出，現在的學生在解決問題時，思維經常會被常規方法步驟所拖累。教師在日常教學中，應經常引導學生學會看清問題的“本質”，透過“局部”要能看到“整體”，而不能將自己的思維禁錮在一個狹小的空間里。

參考文獻：

【1】《數學課程標準（2011）版》[M]，商務印書館，2011：37.