問題導向精準施教

徐波

摘? 要：本節課以問題鏈的形式組織教學，體現了基于情境、問題導向的教學理念，課堂結構鮮明、一氣呵成. 執教教師能夠準確理解教材意圖、精準施教. 特別重視落實對學生進行數學學習一般方法路徑的學法指導，重視發揮“類比”作為一種思維工具的作用，仔細地處理“特殊與一般”“分類與整合”的關系，設計的課堂小結與作業注重開放性、延伸性，反映出教師樹立了正確的教學觀、師生觀.

關鍵詞：類比;一般路徑;學法指導;特殊與一般;問題鏈

本節課執教教師所教授的是人教A版《普通高中教科書·數學（必修）》（以下統稱“新教材”）第二冊第六章第二節“平面向量的運算”中的內容，與《普通高中課程標準實驗教科書·數學4（必修）》（以下統稱“舊教材”）相比，在內容的安排順序上有了一定的調整變化. 執教教師比較準確地捕捉到了新教材中的這些變化，以及這些變化所折射出來的教學含義，精心設計并實施了本節課的教學. 從課堂教學實錄來看，教學效果是很好的.

一、準確理解教材意圖、精準施教

與舊教材相比，新教材把向量的數量積放到“平面向量的運算”這一節中，這就暗示教學要把數量積納入到向量運算的大家庭中，按照學習數學運算的一般方法與路徑來進行學習. 而且新教材增加了一個向量向另一個向量的投影變換，投影的概念也改變了. 這是為了促使學生體會投影是構建高維空間與低維空間之間聯系的橋梁，體會“特殊情況”與“一般情況”的相互作用.

同時，以此建立投影與數量積運算規則之間的關系，為后續學習向量數量積的運算律做鋪墊，提升學生的直觀想象、邏輯推理素養. 執教教師比較準確地解讀了新教材中的這些變化，及其所透露出來的教學啟示，理解到位、施教準確，很好地達成了本節課的教學目標.

二、重視落實數學學習一般方法路徑的學法指導

這節課結合教學內容全面而近乎完美地呈現了數學學習的一般方法與路徑，精心設計并實施了對學生的學法指導. 從課堂上學生的學習表現來看，學生已經非常清楚對“平面向量”這樣一個全新的數學對象，應該從哪些方面沿著怎樣的路徑開展學習. 執教教師很好地處理了“授之以魚”與“授之以漁”的辯證關系，使學生在“學會”的同時也“會學”. 因此，所達到的教學目標是豐富的、全方位的，這與執教教師的教學理念站位高遠有很大的關系.

本節課是這樣體現和落實這一點的.

問題1：前面我們學習了與向量有關的什么運算？

問題2：你能總結研究向量運算的主要路徑嗎？

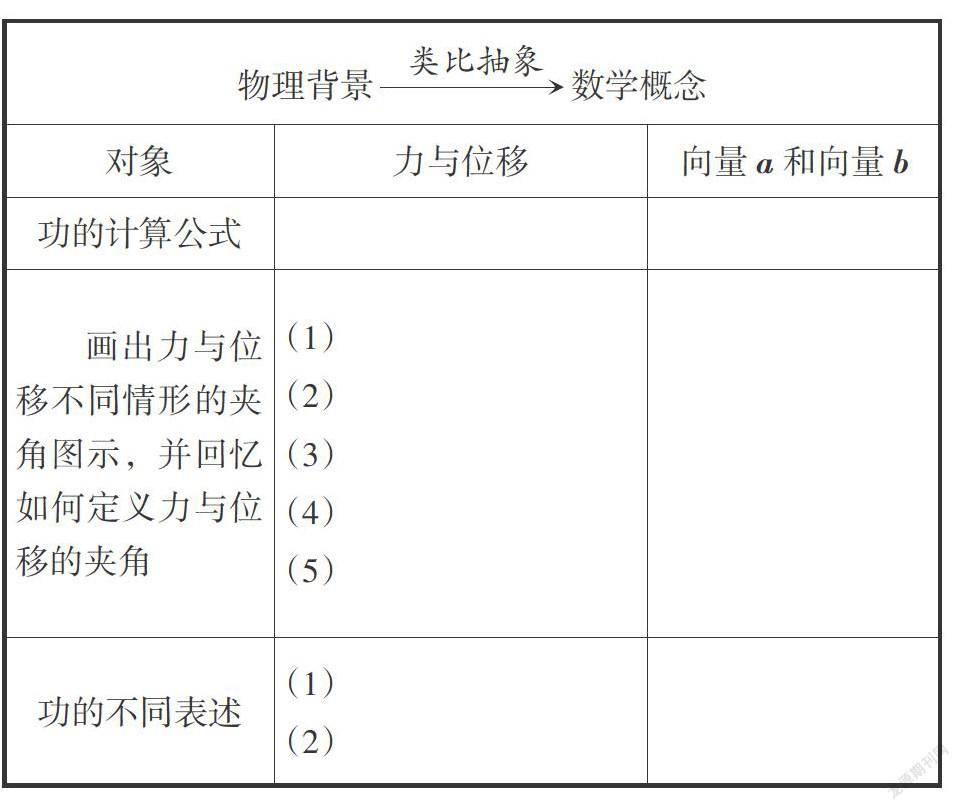
問題3：在下表中填寫與“功”有關的物理問題并思考. 根據表中的物理背景，結合前面所學的向量知識，你能抽象出哪些與向量有關的數學問題？

這樣就緊緊扣住了研究一個新的數學對象的一般方法與路徑，結合具體的學習內容將學法指導落到了實處.

三、重視發揮“類比”作為思維工具的作用

執教教師緊緊抓住了“三個類比”作為思維工具，將這節課組織了起來，使得整堂課“聚精會神”，不僅“神不散”，而且“形也不散”.

這三個類比是：類比數的運算;類比之前學過的向量的線性運算;類比物理的背景.

從學生在課堂上的學習表現來看，學生已經很熟悉類比思維，能夠駕輕就熟地運用類比思維去思考、解決問題，尤其是在類比物理背景方面. 例如，當學生面對“你認為應該如何規定零向量與其他向量的數量積？”“功還有哪些不同表述？數量積呢？”等問題時，表現得非常自如. 可見，“類比”已經內化為學生的思維工具，學生達到了能夠自覺應用的程度. 這同樣是與執教教師在之前的教學中理念深刻、站位高遠是分不開的.

四、重視處理“特殊與一般”“分類與整合”的關系

本節課緊緊抓住了那“五張圖”，也就是銳角、鈍角、直角、零角、平角這五種情況. 先從思考銳角的情形出發，然后再去考慮鈍角、直角、零角、平角的情形，達成了結果在形式上的統一，最后概括，形成概念或者結論. 以此來培養學生縝密的思維，發展學生歸納概括的思維素養，將數學課程的育人價值落到實處.

本節課也特別關注了零向量. 例如，在規定兩個向量的夾角時是不包括零向量的，但是在定義兩個向量的數量積時又是包括零向量的，在定義一個向量在另一個向量上的投影時也是包括零向量的. 這種對零向量的特別關注，給學生留下了深刻的印象.

從學生在課堂上的學習表現來看，在上課過程中學生能始終關注到零向量，在課堂小結環節談學習體會時，學生也談到了思考問題要全面、不要漏掉特殊情況等. 因此，從這個方面也可以看到了數學課程的育人價值的落實情況.

五、重視對課程標準的研讀和新課程理念的落實

問題鏈教學是這節課的靈魂. 本節課精心設計的8個問題所形成的問題鏈，對整堂課的組織結構做出了很大的貢獻.

本節課主要是以問題鏈的形式組織教學，體現了基于情境、問題導向的教學理念，將啟發式、互動式、體驗式等課堂教學方式融為一體，整堂課一氣呵成、暢快淋漓，展現了執教教師過硬的組織課堂教學的功底.

本節課充分體現了執教教師對《普通高中數學課程標準（2017年版）》（以下統稱《標準》）的研讀和新課程理念的落實，對學生的數學學科核心素養的發展多有關照，對培養學生的“四基”“四能”不遺余力. 本節課涉及可以促進學生發展的數學學科核心素養有：數學抽象、邏輯推理、數學運算、直觀想象. 執教教師在做“教學策略分析”時談到“充分重視學生基本數學活動經驗的習得，創設合適的教學情境，盡可能給學生更多的空間和時間，去親身經歷、親自體驗、親手實踐，在教師的引導下，讓每個問題通過思考、交流由學生自己解決”，而且我們看到在課堂教學中執教教師也確實是這樣做的. 學生在課堂學案上各自獨立完成畫圖和練習，學生在黑板上展示自己的結果和思路，尤其是執教教師安排學生互相點評發表觀點，這其實是深度學習的表現，這都反映出執教教師樹立了正確的教學觀、學生觀.

問題鏈教學最難把握的就是一個“度”，《禮記·學記》中寫道：“道而弗牽，強而弗抑，開而弗達”，說的就是這個道理.

六、重視設計開放性的小結與作業

在課堂小結和作業環節，執教教師并沒有按照傳統的教學方式去做，而是體現了自己的獨立思考和創新. 例如，“回顧得出數量積定義的探究過程和研究思路，并表述研究方法，在這個過程中自己的貢獻和收獲是什么？”“類比向量運算的研究脈絡，你知道接下來我們還需要進一步探究數量積運算的哪些問題嗎？”“依據數量積公式能夠實現‘知三求一’的問題，各學習小組自編6道不同角度的問題并規范解答，下節課各小組互相競答板演”等. 不落俗套，這反映了執教教師為落實《標準》付出的努力.

任何數學概念都具有“過程”與“對象”的兩重性，本節課比較強調向量的數量積作為“過程”的一面，而作為“對象”的一面就稍弱些，可能是由于這是第一節課. 相信在接下來的課程中向量的數量積作為“對象”的這一面會得到加強和沉淀，以達到“過程”與“對象”的平衡.

參考文獻：

[1]中華人民共和國教育部制定. 普通高中數學課程標準（2017年版）[M]. 北京：人民教育出版社，2018.

[2]曹才翰，章建躍. 數學教育心理學[M]. 北京：北京師范大學出版社，2006.