等腰三角形中輔助線的作法研究
徐乾平
摘要:本文總結了本人近年來的任教經驗,發現三角形是一大非常常考的模塊。立體幾何方面的問題帶給人的最直觀感受是問題非常的精煉,圖形也非常簡單。在這種條件不充足,圖形表征也不明顯的背景下,很多學生便只是望而卻步了,但學生其實完全可以遇山開山,遇水造橋,這樣問題也能夠順利地得到解決。
關鍵詞:等腰三角形;輔助線;作法
中圖分類號:A 文獻標識碼:A 文章編號:(2021)-27-293
引言
輔助線可以用作擴充題干的已知條件,做輔助線可以使題干當中原有的抽象關系清晰呈現,從而協助學生進行解題。下面是等腰三角形的集中輔助線作法。
一、平移法
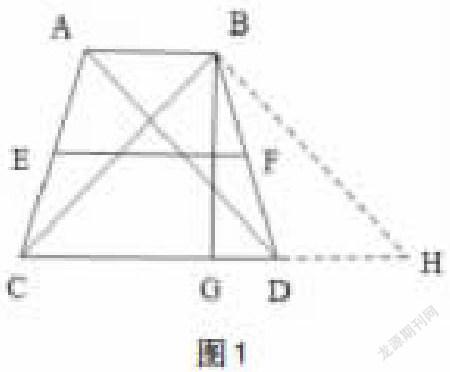
就是將一個點從一個線段之上移動到其他的位置之上,再根據平行線的相關性質,或者是根據平行四邊形的圖形性質,將有關的元素連接起來共同進行推導。例:參見下圖1。已知EF為等腰梯形的中位線,對角線AD和BC之間相互垂直,梯形的高為BG。求證:EF=BG
經過分析題干以及圖形可知,關于AD和BC兩條線段之間只給出了相互垂直這一條件,這就可以從梯形的中位線入手,其論證結論的得出必然與中位線有關。學生便可以自行回憶一下梯形的中位線長度=(上底+下底)*?,因此,如果將AB這條線段的A點沿AD向下平移,直至A點與D點重合,使得AB與DH重合,則梯形的上底+下底=CH。之后連接BH,就得到了一個平行四邊形ABHD,通過梯形的中位線定理便可以完成證明得出結論。
二、旋轉法
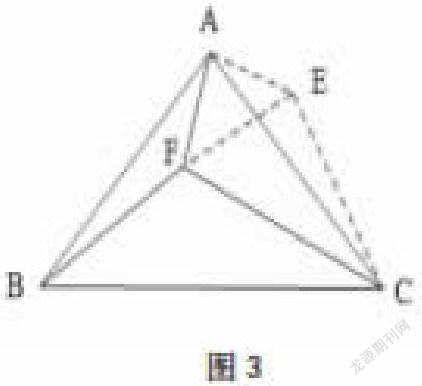
這種方法就是圍繞一個固定的點進行旋轉,旋轉出一個特定的角度,旋轉法主要是利用邊長或者角度相等。對于等腰三角形的論證題目而言,旋轉法顯然應用起來更為方便,值得優先考慮。這種方法可以將分散的條件集中起來,擴展已知的條件,為解決問題和證明結論提供便利條件。但是,由于每個問題的旋轉角度或位置均不相同,學生需要自行想象旋轉后的情況,如果對解題有利,再下筆解答。例:如圖3,已知點F是等腰三角形ABC當中的一點,且AB與AC兩條線段長度相等。已知∠AFB>∠AFC。求證:FC>FB
分析本題,有些學生可能會想到用兩個大小相等的底角分別減去∠ABF及∠ACF得出結論,但是這兩個角的度數我們也無從得知,若想從比較這兩個角的大小入手,便會增加問題的難度。但是如果在圖形當中做出一條輔助線,使得三角形AFB能夠沿著A點逆時針旋轉到三角形AEC的位置之上,即可得出∠AFB=∠AEC,則所有的已知條件便可以聚集在四邊形AFCE之中,再將FE連接得出AFE=AEF,再根據已知條件AEC>AFC,即可得出FC>EC。
三、翻折法
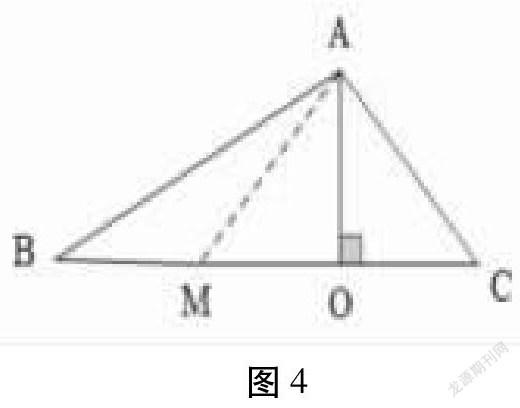
翻折法是指以某條直線作為對稱軸,沿著對稱軸進行對折,得到題目當中給定圖形的全等圖形。在翻折的過程當中,很容易出現等腰三角形,論證過程當中便可以通過這種方式將題目當中給定的零散的線段以及角集中起來,從中獲得更多的等量關系或是已知量。例:如圖4 所示,在三角形ABC當中,∠C的大小是∠B的兩倍,且線段AO垂直于線段BC。求證:BO=AC+CO
X證明:如圖所示,將三角形ACO沿線段AO翻折至三角形AOM的位置上,那么可得出線段AC與AM相等,線段OC與OM相等,∴∠C=∠AMO,兩角均為∠B的2倍,又∵∠AMO=∠B+∠BAM,∴∠B=∠BAM,線段AM與MB相等,又∵BO=BM+MO,∴BO=AC+CO。
結束語
在等腰三角形的證明題的解題過程中,僅僅通過既定條件并不能很輕松的完成證明,而輔助線的添加便可以很輕易地解決解題難的問題,從而節省很多的時間以及精力。再結合上述的三種輔助線作法,相信一定能給學生帶來很大的幫助!
參考文獻
[1]趙勝.等腰三角形中輔助線的作法淺析[J].科教文匯(中旬刊),2017,{4}(04):100-102.
[2]劉巍.等腰三角形中輔助線的作法[J].數理天地(初中版),2016,{4}(03):15-16.

