為數學教學插上翅膀
蔣素芳
在多年的初中數學教學中,筆者總覺得學生在上七年級(上)4.1《用字母表示數》的時候,學生特別感興趣,那是由于數學課堂上教師常用多媒體播放一些數學動畫及兒歌,這些都能將學生帶入神奇有趣的數學世界。
一、新課課堂學習中多媒體之“有趣”
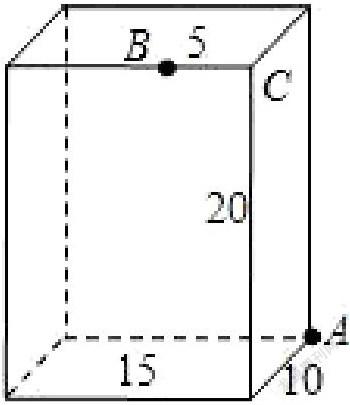
數學課中出現大量的“討論”,如:《勾股定理》這一課中有這樣一個習題:長方體的長為15,寬為10,高為20,點B離點C的距離為5,一只螞蟻如果要沿著長方體的表面從點A爬到點B,需要爬行的最短距離是多少?將學生分組后將問題帶回家思考。
討論:1.求兩點間的最短距離你想到什么?
學習經過討論后得出:兩點間的最短距離是連接這兩點的線段的長度。
2.題中螞蟻是沿長方體表面爬行,能否直接連接這兩點?
經過學生討論后在課堂上,教師可利用多媒體演示,將長方體表面展開。
3.除了這種展開方式,還有其他的展開圖嗎?
因為學生回家已經進行了思考,有些組的代表利用多媒體將自己的的成果進行展示,顯得非常清晰明了,共得到三種類型的展開圖。
4.你能利用這些展開圖計算最短距離嗎?
5.哪個距離才是我們這道習題的最短距離?
二、實驗課堂學習中凸顯多媒體之“有利”
如:在講授《直線和圓的位置關系》這一課時的時候,利用多媒體技術可以使直線轉動,產生與已知圓的相離、相切、相交的各種動態的位置關系,并在旁邊顯示圓的半徑(R),并動態的顯示圓心到直線的距離(d),學生們可以一目了然的動態的了解到直線與圓的位置關系,與圓的半徑(R)、圓心到直線的距離的數量關系,使學生在觀察實驗的同時,推出直線和圓的位置關系與圓的半徑、圓心到直線的距離之間的關系。
如:在講授等腰三角形“三線合一”時,因傳統教學較難展現其發現過程,給學生的理解造成一定的難度。利用《幾何畫板》軟件,則可以在屏幕上作出等腰ΔABC及其頂角∠A的平分線、BC邊上的高和BC邊上的中線,用鼠標在屏幕上拖動ΔABC的頂點A,改變ΔABC的大小和形狀(但始終保持其為等腰三角形)。此時,等腰ΔABC和"三線"在保持依存關系的前提下隨之變化而變化,但在移動的過程中,學生會直觀地發現存在這樣的點A,使得等腰三角形頂角的平分線、底邊上的高和底邊上的中線三線重合。
三、復習課堂學習中展示多媒體之“有效”
傳統的復習課教學中,教師把大量時間花在語言描述和板書等方面。語言陳述過多,學生抓不住重點,前后內容聯系困難。而應用多媒體教學,可以將本章的知識點逐個呈現出來,構建出“知識樹”。
“代數式”這部分教學內容特點:基本概念多,必須記憶的多,實際運用的多,題型變化多。通過多媒體課件呈現上面的“知識樹”,學生能將本章的知識要點清晰地記住。
縱觀近幾年的中考試題,有關動點問題的綜合試題,學生比較薄弱。若采用傳統的教學,老師板書、畫圖、抄例題耗費大量寶貴的學習時間,而且可視性差,在一節課內容量較小的情況下,教學效果也會受到影響。
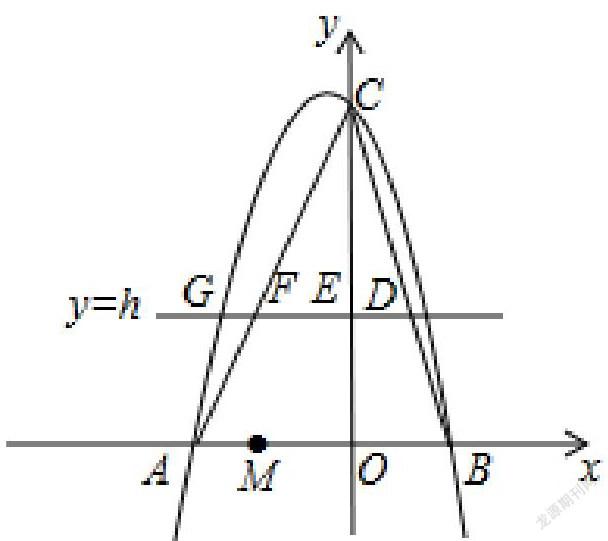
如:“二次函數”綜合題
例1:如圖,在平面直角坐標系中,拋物線y=ax2+bx+6經過點A(-3,0)和點B(2,0).直線y=h(h為常數,且0 (1)求拋物線的解析式; (2)連接BE,求h為何值時,△BDE的面積最大; (3)已知一定點M(-2,0).問:是否存在這樣的直線y=h,使△OMF是等腰三角形?若存在,請求出h的值和點G的坐標;若不存在,請說明理由。 總之,在現代教學中利用多媒體技術是提高課堂效率的一種有效手段。但在教學中一定要突出學生的主體地位,“教師的用”與“學生的用”要有機的結合,這樣才能真正促進學生自主地參與到課堂教學活動中。 參考文獻: [1]初中《數學》(7-9年級)教科書、教師教學參考用書、新課程標準 [2]王道俊.教育學[M]北京:人民教育出版社

