2020年全國數學中考“隱圓”問題探究

梁志堅

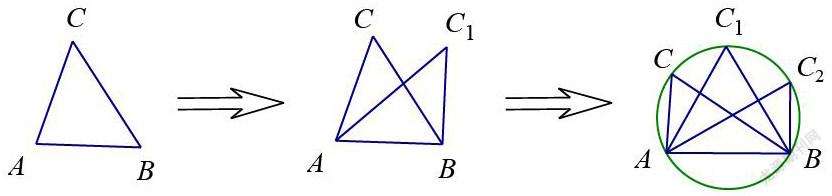
一、問題的提出

圓是初中數學“圖形與幾何”模塊中最重要的內容之一. 縱觀近年來全國各省市中考試題，圓的考查形式往往有兩種：一種是題干中給出圓，以圓為背景命制試題;另一種是題設中沒有圓，但在解題過程中，需要構造圓，利用圓的相關知識來解決問題. 我們稱第二種為“隱圓”問題。

二、問題的研究

（一）“隱圓”問題類型

類型一. 四點共圓型

初中階段常見的四點共圓模型有：

1.根據定義：到定點距離等于定長的點共圓（如圖1）;

2.共斜邊的兩個直角三角形的頂點共圓（如圖2）;

3.對角互補的四邊形頂點共圓（如圖3）;

4.同一線段同側所對角相等，角的頂點與線段兩個端點共圓（如圖4）。

類型二. 路徑（軌跡）為圓（弧）型

動點問題是全國數學中考命題的熱點，其命題形式大致分為兩類：

1. 任務型動點：由雙動點與圖中的一至二個定點組成的圖形，滿足條件：（1）構造成特殊三角形或四邊形;（2）與圖中已有三角形全等或相似;（3）圖形的周長或面積成一定比例關系或是獲取最值;（4）構成一定度數的角;

2. 圖形在進行平移、軸對稱、旋轉這三種基本幾何變換過程中，圖形中某一特殊點（常為中點）的路徑問題，或是與這一點相關的第一類問題. 而這一特殊點的路徑，通常有兩種情況：一是直線型（線段），二是圓（弧）型。

（二）“隱圓”問題解題方法研究

2020年全國數學中考與“隱圓”有關的試題，考查的核心數學思想是轉化，考查的熱點問題是求最值. 最值問題又分為二類：一是求線段長的最值;二是求三角形面積的最值.鑒于四點共圓問題前面已有較為詳細的論述，所以本環節側重闡述最值問題、倍角（半角）問題、定角對定弦問題。

1. 最值問題：

圓中最值問題，有個最核心的“元”模型——“一箭穿心”，如圖9：

“尋模型——現隱圓——明路徑——解最值”，是這類問題的解題思路與過程. 另外，特別強調的是，在圓中取弦的中點，與圓心構造成三角形的中位線，是非常重要的一種作輔助線的方法，這種方法在高中立體幾何中證明線、面平行，也經常用到。

2. 倍角與半角問題

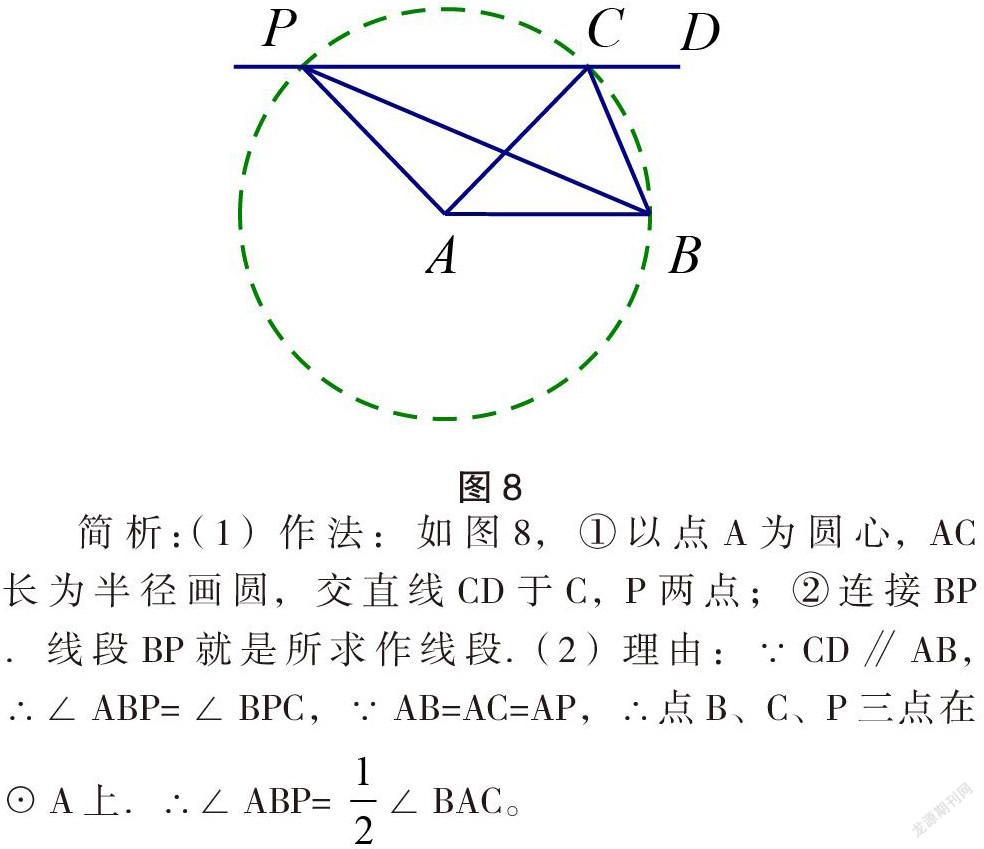
在一些二次函數綜合題中，會出現“不定角”問題. “不定”，是指角的位置不明確，解題時，有時需要通過構造圓，利用圓周角的性質，來進行角的轉化。

根據倍角或半角關系，構造“隱圓”，是中考“隱圓”問題中難度最大的一類，需要教師在平常教學中，尤其是數學尖子生培訓過程中，經常滲透這種轉化的思想與方法。

3. 定角對定弦問題

“定角對定弦”問題有顯性且確定的模型，其本質如下：

（1）若△ABC的邊AB確定，∠C的大小確定，則點C為△ABC外接圓上（不與A、B重合）一動點，△ABC的形狀并不確定，如下圖：

（2）“定角對定弦問題”，通常是求路徑長，當我們明白（1）中的實質之后，就很容易辨識問題的本質并快速找到解決方法：先確定△ABC外接圓，再求半徑，最后求路徑長（弧長）。

（三）“隱圓”問題教學導向

中考試題是教學的導向標. “隱圓”問題對初中數學教學有何教學導向呢？

1.教學要圍繞核心素養，培養學生思維能力

真正的學科素養，不應只是一些文本的知識，應是內化為學生意識中的一種涵養與關鍵能力. “隱圓”問題，是學生較深入掌握圓的知識后，對相關知識與方法靈活運用的一種綜合性考查，教師在初三數學教學中，應重視這類問題的教學研究，培養學生的思維能力。

2.辯證的看待“問題模型”

近幾年，關于數學問題的模型，各類雜志、自媒體、網絡平臺均有較大力度的宣講，有些甚至歸納出上百個模型. 目前，在全國較大的一些數學教師研究群里，對問題模型教學也有較大的爭議，不少教育專家反對過多的模型教學，認為這樣會拘束學生的思維發展。筆者認為，問題模型教學契合數學核心素養中的“建模思想”，對學生較快掌握某一模塊或專題有較大的促進作用，但要注意兩點：一是不能過多，否則學生會淹沒在模型中迷失方向;二是不能死記模型，必須讓學生真正明白模型的來源、原理. 下面以“隱圓”最值問題的“元”模型為例，闡述模型如何講透數學道理。

PA為什么最短？PB為什么最長？教師可以向學生講清楚這個道理：

如圖10，點C為⊙O上任意一點（不與點A重合），在△POC中，OC+CP>OP，即OC+CP>OA+AP，因為OA=OC，所以CP>AP. 同樣可證明PB>PC。

3.加強單元復習中的專題教學，重視內容設計的“生長性”

復習不是知識、方法的簡單重復，而是自主建構、不斷知新、不斷生長的過程。專題復習聚焦核心內容、核心思想方法，它應具有以下三個特征：

（1）生長性. 所謂生長性，由元問題出發，基于基礎與經驗，在解決問題過程中不斷產生新問題，不斷生長新的數學知識、方法、思維、經驗。

（2）結構性.專題復習主要關注知識在不同領域的內在聯結，或通過知識聯結載體，或通過某一思想方法聯結載體。

（3）層次性.專題復習主題明顯，思維要求較高，目標定位不清晰會導致“專、深、難”，中等生與學困生不能接受. 因此在內容設計時，要體現高立意、低起點，關注不同層次學生的發展，從而激活思維動力，增長思維活力。

參考文獻：

[1]楊軍.巧用點線命題凸顯素養考查[J].中學數學參考，2019.4中.54-56.

[2]姜曉翔.初中數學命題方法之延續策略[J].中國數學教育，2019.6.39-41.

[3]中華人民共和國教育部.義務教育數學課程標準（2011年版）[S].北京：北京師范大學出版社.

[4]戴娟.微專題在中考數學第二輪復習中的實踐與思考[J].中學數學月刊（蘇州），2018.11.23-25.

[5]錢云祥.源自教材基于課堂劍指素養[J].中學數學雜志（曲阜），2019.8.54-55.

廣州市番禺區毓賢學校 廣東 廣州 511430