基于連續型信息熵的海上突發事件應急資源配置量研究

何鋮 楊春林 曹月

摘 要：針對海上突發事件救援對應急資源的需求，使得岸上儲備基地的應急資源配置量維持在合理水平內，本文結合海況、災情演變等因素，綜合考慮儲備基地所轄事故區域內應急資源配置過量或不足產生的總成本，構建了基于連續型信息熵的應急資源配置量模型，通過算例對模型的有效性進行驗證，并進行決策者風險偏好和最優配置量之間的靈敏度分析。研究結果表明，基于連續型隨機變量的信息熵模型可為決策者提供應急資源的最優配置量，并且最優配置量隨決策者風險偏好的不同趨于穩定。

關鍵詞：海上突發事件;信息熵;應急資源;配置量

中圖分類號：F224 ? ? ? ? ? 文獻標識碼：A ? ? ? ? ? ?文章編號：1006—7973（2021）07-0072-04

由于氣象、水文等眾多不確定性因素，海上突發事件的救援中對于應急資源的需求存在不確定性，為保障未來一段時期應急救援的順利進行，須在特定區域內配置必要的應急資源。應急資源配置過量將產生閑置成本，配置量不足則不能及時滿足救援要求。因此，確定合理的應急資源配置量至關重要。

迄今為止，針對應急資源配置量問題，國內外學者立足于不同視角，運用模糊數學、魯棒優化、信息熵等理論方法進行了廣泛而深入的研究。周禮勝[1]構建了基于模糊層次分析法的應急物資分類模型和基于信息熵的應急物資儲備量模型。Tufeckci Suleyman 和A.Wallace William [2]將應急資源看作折中利用問題，利用多目標復雜優化模型解決。Heung Suk Hwang [3]提出了應急救災模型，有效解決了朝鮮饑荒應急資源的庫存控制、供應有效性等一系列問題。F.Fiedrich [4]等建立單目標多個限制條件模型，用以解決地震后應急資源優化配置問題。張玲[5]考慮供應點應急資源的總投入和調度費用，建立了應急資源配置的兩階段模型，利用魯棒優化方法對不確定需求的應急資源配置問題進行求解。陳超[6]構建了需求總量預測的概念模型，確定受災區與儲備點的吸引力指數，分別預測出各儲備點的應急資源需求量。

基于現有文獻分析，大多數文獻運用運籌學理論確定應急資源配置量，使用信息熵理論求解應急資源配置量問題中，也多采用離散型隨機變量的信息熵建立數學模型。針對海上突發事件的特點，信息熵理論可解決類似不確定性系統中的應急資源配置量問題，同時，應急資源的需求量隨著事件的等級、性質以及時間等因素進行連續性變化。因此，本文基于連續型隨機變量的信息熵的理論，考慮儲備基地應急資源配置量不足與過量造成的影響，找到二者之間的平衡點，將應急資源配置的不確定轉化為確定性的問題，從而定量地解決事故區域范圍內的應急資源的配置量問題。

1問題描述

海上突發事件發生后，根據相應救援信息，應急資源從岸上儲備倉庫持續運輸至事故區域，當儲備倉庫的庫存不足時，應急資源從供應點運輸至事故區域。同時，供應點為儲備倉庫定期或定量地補貨，保證儲備倉庫為事故區域的持續供應。根據各配置主體間的關系，事故區域的應急資源需在最短時間內從儲備倉庫調出。然而，海上突發事件的不確定性，管理人員無法準確預測突發事件的等級、數量以及應急資源的種類和數量，導致儲備倉庫的應急資源配置過量或不足。因此，管理人員需權衡儲備倉庫的庫存，確定最佳的應急資源配置量。

2連續型變量的應急資源信息熵模型

由于影響儲備倉庫應急資源配置量的因素眾多，為符合實際，對模型成立的前提條件作如下假設。

2.1模型假設

（1）各類應急資源的種類已知且本文僅考慮一種應急資源的配置量;

（2）考慮一定周期內儲備倉庫的應急資源配置量;

（3）僅研究應急資源的配置總量，不考慮各個儲備倉庫具體的分配量;

（4）應急資源需求量為連續型隨機變量，配置量為離散型隨機變量;

（5）根據海上突發事件的特點，應急資源的缺貨成本遠比閑置成本產生的影響大，故引入懲罰系數放大缺貨成本。

（6）考慮到計算的復雜度，故假設應急資源配置過量和不足時，成本均呈線性增長。

2.2符號說明

2.3模型建立

應急資源需求量X隨著海上突發事件的演變而不斷變化，假設服從正態分布。若連續型隨機變量X的概率密度函數為p（x），且滿足，log對數取e為底，則該連續性系統的信息熵表示為：

表示關于應急資源最優配置量的信息熵函數（），它描述應急資源配置量的不確定性程度。當越小，應急資源的配置量就越趨于一個確定值，總成本也相應地達到最小值。由此，當趨向于0時，可求出，即最優配置量。

3.2算法設計

上述數學模型同時含有對數的反常積分，利用微積分基本定理等數學原理求解的計算復雜度高。由于事故區域的應急資源需求量呈動態變化，最終確定的配置量可為滿意解，現代啟發式算法可高效求出滿意解，Hollstein R.B.（1971）最先嘗試將遺傳算法應用于函數優化問題，其在求解函數優化問題有較好的收斂性，可迅速求出近似的滿意解。因此，本文根據實際微積分數學模型，設計遺傳算法求解，具體步驟如下所示。

（1）種群采用實數編碼，確定種群規模N，初始種群在配置量的上下限中隨機產生，隨機生成的個體作為初始種群X（0），設t=0。

（2）計算X（t）中個體的適應值，將目標函數作為適應度函數。

（3）根據適應值的大小從X（t）中選擇若干個較小的個體作為進化群體X1（t）。選擇函數用matlab算法工具箱中的Stochastic uniform（隨機均勻分布），根據其降落的位置確定下一代的雙親。

（4）在群體X1（t）上按照0.99的交叉概率和0.01的變異概率進化，交叉和變異函數選擇Constraint dependent即約束相關，有無約束時為均勻選擇，有約束時為自適應種群，生成能夠滿足約束的種群。本文求解最小值，為避免超級個體的影響，按照錦標賽法選擇N個個體最為下一代種群X（t）。

（5）由于本文中的函數優化問題已知，即要求應急資源最優配置量的信息熵最小，可采用當前最優值與問題的最優值之差（）作為終止準則，其中是最優值，是容許誤差。是否滿足終止準則，如果滿足，停止計算。否則返回第二步。

4算例分析

山東海事轄區呈現典型的“七區八線”水上交通格局，山東境內的7個港區與對外的8條主要航線形成多處交通流的交匯區。交匯區內船舶相遇頻繁，航線和航速突變，轄區內礁石、淺灘等障礙物以及成山角至石島一帶的自然環境，成為影響船舶通航的安全隱患。因此，山東海事轄區的海上突發事件多發，應急資源的需求量較大，確定山東海事轄區的應急倉庫的配置量是一個值得研究的問題。以溢油分散劑（以下稱消油劑）的配置量為例，代入連續型信息熵模型，求解最優配置量，并通過敏感性分析觀察懲罰系數與最優配置量的聯系。

根據實際情況，消油劑的市場價格為9900元/噸，假設消油劑在應急倉庫中的年單位庫存固定成本約為其價值的9%，日常庫存中的單位損耗成本約為其價值的2%，。而當儲備的消油劑數量不足時，單位臨時調運成本約為價值的20%，漲價的機會成本約為價值的1.2倍。令消油劑本身的價值為C，則由以上假設可得到以下數據關系：

通過歷史數據，確定消油劑的配置量的上下限，山東海事轄區近十年消油劑需求量分布如表1所示。

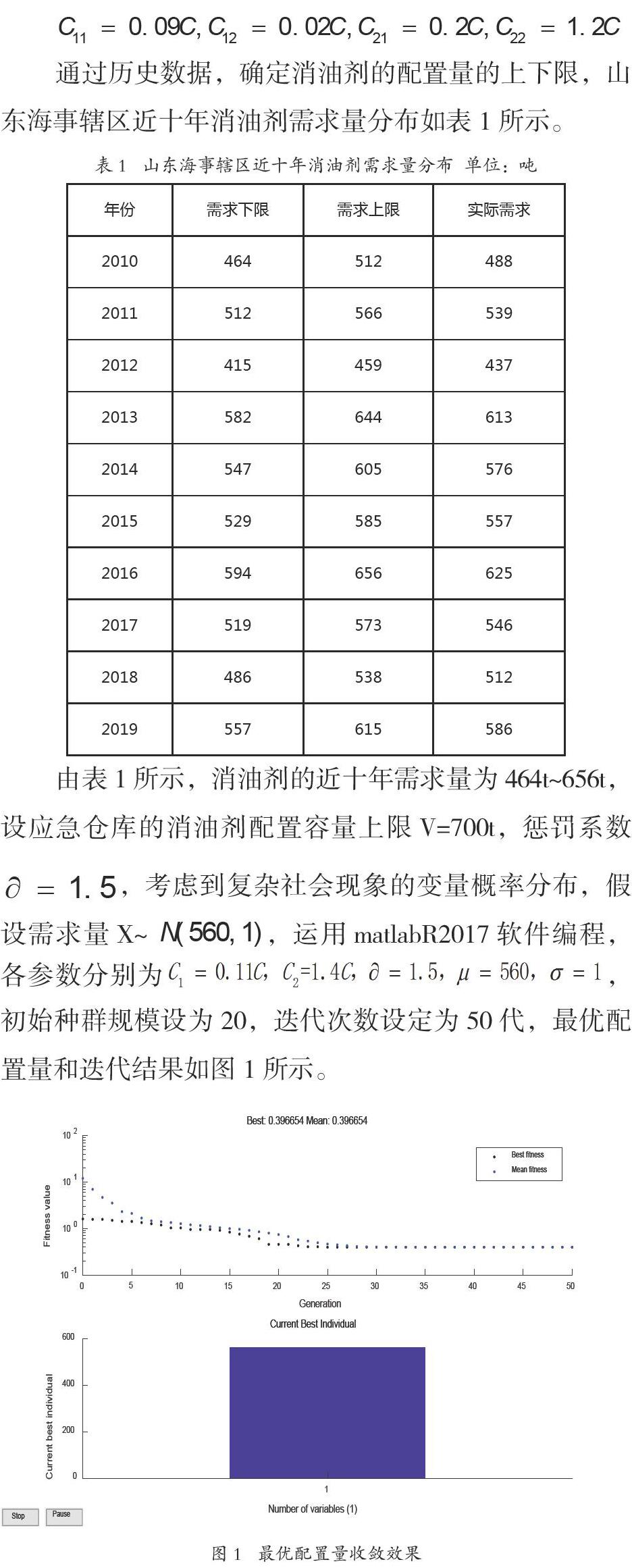
由表1所示，消油劑的近十年需求量為464t～656t，設應急倉庫的消油劑配置容量上限V=700t，懲罰系數，考慮到復雜社會現象的變量概率分布，假設需求量X～，運用matlabR2017軟件編程，各參數分別為，初始種群規模設為20，迭代次數設定為50代，最優配置量和迭代結果如圖1所示。

由圖1可知，在28代之后圖像收斂，最優配置量m* = 562.1067，信息熵值= 0.3967，信息熵趨向于0，表明不確定性的連續系統轉化為確定的數值，即求得的結果可作為應急倉庫的最優配置量。綜上所述，為同時滿足救援需求和減少消油劑的過多浪費，可將消油劑的一年庫存量定為562.1067噸，最終的庫存量可根據實際情況在最優配置量基礎上左右小幅度波動。

5 總結

本文針對海上突發事件的不確定性，考慮應急資源配置過量和不足產生的總成本，建立基于連續型隨機變量的信息熵模型，確定了應急倉庫一定周期的最優配置量。同時，考慮決策者的風險偏好，通過懲罰系數控制不同水平的最優配置量，結果表明，連續性隨機變量的信息熵模型應用于海上突發事件的應急資源配置量的求解穩定性強。為了簡化模型，本文假設缺貨成本隨需求量變化呈線性增長，非線性增長的情形對最優配置量的影響以及多倉庫間協同配置問題將是本文繼續研究的方向。此外，本文可為應急資源配置主體提供輔助決策，提高應急資源管理水平。

參考文獻：

[1] 周禮勝.基于模糊層次分析法和信息熵的應急物資庫存管理研究[D].中國科學技術大學，2010.

[2]Suleyman T，William A W.The emerging area of emergency management and engineering[J].IEEE Transaction on Engineering，1998，45（2）：103-105.

[3]Hwang H S.A Food Distribution Model for Famine Relief[J].Computers& Industrial Engineering，1999，37：335-338.

[4] Fiedrich F， Gehbauer F， Rickers U. Optimized resource allocation for emergency response after earthquake disasters[J]. Safety Science， 2000， 35（1）：41-57.

[5] 張玲.不確定需求下應急資源配置的魯棒優化方法[J].系統科學與數學，2010，30（10）： 1283-1292.

[6] 陳超.自然災害應急物資需求分類及需求量研究[D].北京：北京交通大學， 2011.