立足問題知識考點探究破題解析視角

常燕

[摘 要]二次函數與直角三角形問題的突破存在一定難度，需要學生把握知識考點，靈活選用解法來構建解題思路.總體而言，可從幾何、代數兩大方向進行問題探究，充分利用直角三角形的勾股定理、斜率之積為-1的幾何意義來解題.

[關鍵詞]二次函數;直角三角形;勾股定理;斜率

【真題探究】

2020年江蘇省徐州市中考數學的壓軸題以二次函數與直角三角形為背景，其解析方法具有一定的代表性，下面筆者對其進行深入剖析.

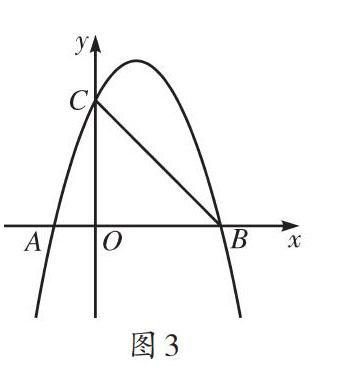
考題：（2020年徐州市中考數學卷第28題）如圖1所示，在平面直角坐標系中，函數[y=-ax2+2ax+3aa>0]的圖像交[x]軸于點[A]、[B]，交[y]軸于點[C]，它的對稱軸交[x]軸于點[E].過點[C]作[CD∥x]軸交拋物線于點[D]，連接[DE]并延長交[y]軸于點[F]，交拋物線于點[G].直線[AF]交[CD]于點[H]，交拋物線于點[K]，連接[HE]、[GK].

（1）點[E]的坐標為 ;

（2）當[△HEF]是直角三角形時，求[a]的值;

（3）[HE]與[GK]有怎樣的位置關系？請說明理由.

解析：考題為二次函數壓軸題，第（2）問探究[△HEF]為直角三角形時a的取值，下面主要探究該問的解法，不對第（3）問深究.該問涉及點E，有必要先求解（1）問中點E的坐標.

（1）點E是拋物線對稱軸與x軸的交點，由拋物線的解析式可知其對稱軸為[x=-2a2×（-a）=1]，則點E的坐標為（1，0）.

（2）該問設定了眾多的相交條件，根據交點求法即可求出關鍵點的坐標，將其表示為與a相關的點坐標.探究[△HEF]為直角三角形時a的取值可采用代數法，由點坐標求線段長，分類討論不同情形下由勾股定理構建的方程.

評析：上述在突破二次函數與直角三角形問題時采用了代數法，即利用兩點之間的距離公式求解三角形的邊長，分三種情形討論直角三角形，由勾股定理構建與坐標參數相關的方程，從而完成求解.該種方法的思維過程較為簡單，但計算過程相對較為復雜，解析突破時需嚴格論證，精準求解.

【解法拓展】

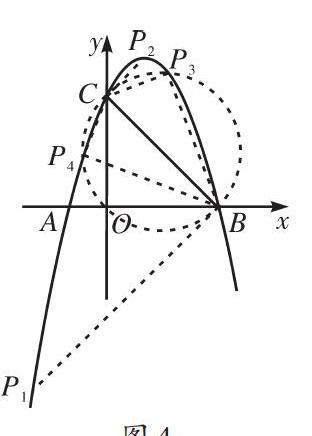
對于二次函數與直角三角形問題，還可從幾何視角構建解題思路，若坐標系中兩直線相垂直，則直線的斜率之積為-1，具體原理如下.

解析：上述為直角三角形探究題，點P為拋物線上的動點，題干沒有設定直角頂點，則需要分別討論點A、B和P為直角頂點的三種情形.可采用幾何法，從斜率角度分別探討.由于動點P位于二次函數圖像上，可通過“兩線一圓”來繪制圖像，則具體步驟如下.

評析：上述在解析二次函數與直角三角形問題時采用了幾何解析法，以相互垂直直線的斜率之積為-1來構建方程，然后分類求解點坐標.問題解析的難點主要在模型構建上，函數背景中特定條件下可構建不同的直角模型，會造成多解情形，此時就需要論證直角模型.合理利用幾何圓的特性，利用隱圓建模是數學的常用方法，解題時可靈活運用.

【解后反思】

1.挖掘問題考查點，生成程序性解法

二次函數與直角三角形中考壓軸題的設問形式較為多變，但考題所涉及的內容是固定的，知識考點有規律可循.往往考題涉及的知識點包括拋物線與直線的交點坐標、直線解析式、勾股定理、三角形相似的性質、兩線垂直條件等.可綜合運用函數與方程思想、數形結合思想、分類討論思想來破解問題.教學中教師可引導學生深入挖掘考點，總結類型問題的解題思路，如二次函數與直角三角形問題可按照“設點找點→分類建模→構建方程→解點求值”的流程突破，教師可結合具體問題，幫助學生生成程序性解法.

2.挖掘解法原理，深入拓展探究

上述對二次函數與直角三角形問題開展解法探究，生成了代數法與幾何法兩種解題方法，每一種方法背后都隱含著對應的數學原理，因此深入挖掘解法原理是教學的關鍵.教師可立足基本問題引導學生理解幾何法中利用斜率乘積構建思路的幾何意義，以及代數法中由勾股定理構建方程的本質內涵，從而使學生從根本上掌握解題方法.另外，教師有必要對類型問題的解法進行拓展探究.以上述問題為例，除了利用勾股定理和斜率之積來構建思路，還可利用幾何相似，通過直角三角形相似來挖掘垂直關系，求解推導.

3.關注思維發展，設問引導探究

考題探究是提升學生解題能力的重要方式，而在探究過程中應重點關注學生的思維活動，以發展學生思維為目的.如上述考題教學中有必要立足考題結構，引導學生思考問題考查點，結合圖像進行條件推理，思考解析方向.教師在探究環節要合理設問，準確把控探究方向，啟發學生思考，同時可引導學生適度聯想，對比解題方法，有意識地培養學生思維的連續性.

（責任編輯 陳 昕）