《全等三角形的再認識》教學案例與思考

洪莎莎

[摘 要]全等三角形是初中幾何學習的重要內容之一，也是研究四邊形、圓等幾何圖形的重要工具.但是，不少學生無法在復雜的幾何圖形中找到全等三角形，因而不能解決相關問題.有很多全等三角形模型是相同的，如果將這些模型看作“基本圖形”，通過“基本圖形”的認識、分離、構造，可以提升學生解決問題的能力，提高解題效率.

[關鍵詞]全等三角形;基本圖形;構造

全等三角形是初中幾何學習的重要內容，借助全等三角形可以幫助學生解決線與線、角與角之間的關系的問題.反之，通過線與線、角與角之間的關系可以找到全等三角形，并進一步對相關三角形開展研究.可以說，全等三角形是幾何元素點、線、面的載體，通過這個載體又可以更好地研究點、線、面.不僅如此，全等三角形也是研究四邊形、圓等復雜幾何圖形的重要工具，因此全等三角形的學習十分重要.但是，在學習過程中，除了一些比較簡單的三角形外，不少學生無法找到全等三角形，因而也就不能解決相關問題.在教學過程中，筆者發現有很多的全等三角形模型是相同的，如果將這些模型看作“基本圖形”，通過“基本圖形”的認識、分離、構造，可以提升學生解決全等三角形問題的能力，有效提高解題的效率.

一、教學目標及重難點

1.教學目標

（1）復習全等三角形的相關知識，認識全等三角形中的基本圖形，能根據其位置關系進行分類;

（2）從復雜的幾何圖形中把基本圖形分離出來，并解決問題;

（3）能構造基本圖形，并解決問題.

2.教學重點

能從復雜的幾何圖形中分離出基本圖形并解決問題.

3.教學難點

（1）能從復雜的幾何圖形中分離出基本圖形并解決問題;

（2）能構造基本圖形解決問題.

二、教學過程

1.創設情境，認識基本圖形

問題設計：已知△ABC，畫一個三角形和△ABC全等.

設計意圖：

（1）通過畫全等三角形，幫助學生復習全等三角形的相關知識;

（2）展示學生畫出的全等三角形，讓學生觀察并分類，然后提出全等三角形中的“基本圖形”，讓學生認識全等三角形這一類的基本圖形，同時通過為基本圖形分類，加深學生對基本圖形的認識;

（3）在進行活動一時，提出三個問題：①你是怎么做的？②你這樣做的依據是什么？③你還有更加簡便的做法嗎？通過問題①②，有助于學生對全等三角形知識的復習;通過問題③，學生應該可以想到從位置關系入手，從而畫出平移、翻折和旋轉所得到的全等三角形，這樣與全等三角形有關的基本圖形就得到了（如圖2、圖3、圖4）.

2.解決問題，分離基本圖形

設計意圖：做前提問：①你能找到基本圖形嗎？②你是怎么找到基本圖形的？旨在歸納、總結如何從復雜的幾何圖形中分離基本圖形，關鍵是要標注已知條件，從而可以快速分離基本圖形，這樣就可以方便解決問題.第（1）小題讓學生回答后做小總結，第（2）（3）小題讓學生模仿解答，讓學生掌握分離基本圖形的方法——在圖形上標注已知條件.分離出每一小題的基本圖形（如圖8）后再讓學生總結，發現都與前面所畫的全等三角形的某種模型相同，體現出了研究的必要性.

設計意圖：此題其實是上題中（2）（3）小題基本圖形的合成.主要讓學生感受到幾何圖形就是由基本圖形所構成的，有的時候可能是一個，有的時候可能是兩個甚至是多個.關鍵是要把基本圖形分離出來，才能更好地解決問題.另外，通過本題，也可以讓學生進一步掌握基本圖形分離的方法.

3.拓展提升，構造基本圖形

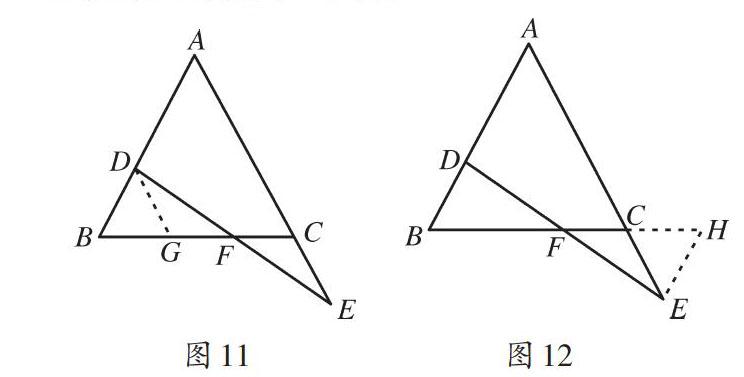
設計意圖：通過前面活動，學生會識別基本圖形，并能從復雜的圖形中分離出基本圖形.此活動則是讓學生構造基本圖形，將復雜的題目變簡單，從而高效、正確地解決問題.本題中 DF與EF所在三角形并不全等，但這兩個三角形中有相等的邊與角，要想利用全等三角形證明，就要想辦法構造出全等三角形.在構造過程中，結合題目中所給條件，總結出以下幾種方法：

三、教學思考

全等三角形是研究幾何圖形的重要載體，是否能夠有效利用全等三角形解決問題，取決于學生是否能夠找到全等三角形.為了幫助學生在復雜、多變的幾何圖形中發現全等三角形，本節課通過總結全等三角形中的“基本圖形”入手，讓學生借助熟悉且常見的基本圖形，快速找到全等三角形，并解決問題.在教學過程中，問題一環連一環，內容逐漸深入，探究的方向明確、方法明朗、節奏明快、效果明顯.

[? ?參? ?考? ?文? ?獻? ?]

[1]? 曹彩華.“與三角形有關角及角的等分線”教學設計與思考[J].中學數學教學參考，2020（Z3）：26-27.

（責任編輯 黃桂堅）