師范認證背景下實變函數(shù)習題課的教學探討
——以集合可測的條件探討及其應用為例

王 文，周 輝，余 靜

(合肥師范學院 數(shù)學與統(tǒng)計學院，安徽 合肥 230601)

培養(yǎng)學生的數(shù)學核心素養(yǎng)不僅是中學課堂的重要目標，也是大學課堂的重要目標。針對師范生課堂教學來說，培養(yǎng)學生的數(shù)學核心素養(yǎng)也是教育部對師范專業(yè)師范認證的重要指標之一。如何培養(yǎng)學生用數(shù)學的眼光觀察問題、用數(shù)學的思維分析問題、用數(shù)學的思想解決問題是課程改革理念的一項重要任務，也是師范生教學能力培養(yǎng)的重要目標之一。而問題是數(shù)學的靈魂，如何培養(yǎng)學生提出問題、分析問題、解決問題的能力，從問題的特殊情形抽象出一般結論的能力是大學數(shù)學教學關鍵點，也是落腳點。

在實變函數(shù)教學中，測度就是長度概念的一個推廣，在實數(shù)集R中能夠量出長度的點集是很少的，因此，需要把長度的適用范圍擴大，使更多的集合具有一定意義的長度，也就是所謂的測度。類比長度公理，數(shù)學家Lebesgue提出了測度公理[1]，就是保留了長度公理中的非負性和正則性，將其中的有限可加性推廣到可數(shù)可加性。

那么如何找出具有這些性質(zhì)的測度m以及關于m的可測集類呢？首先引進外測度，外測度對R中的任意點集都有定義，滿足非負性和正則性，但不一定滿足可數(shù)可加性。然后，對外測度的定義域加以約束，即在R中找某一集合類μ，使得外測度在μ上滿足可數(shù)可加性。此時，μ中的元素就稱為可測集，可測集的外測度也就是它的測度了。

本文主要探究如何引導學生自主探尋可測集的判定條件。

1 可測集的判斷條件

從可測集的定義出發(fā)，有目的地引導學生探尋集合可測的判定條件，是探尋實變函數(shù)教學改革的目標之一，更是師范類院校培養(yǎng)師范生教學技能、引導學生深挖教材的重要手段之一。下面以總結歸類的方式進行啟發(fā)式探討。

目標： 探討集合可測的判定條件以及充要條件。

設計思路一從簡單的可測集類出發(fā)，先引導學生給出簡單集合可測的判定條件，并簡單給出理由，比如外測度為零的集合。

結論1外測度為零的集合可測。

證明?T?Rn，有m*T≤m*(T∩E)+m*(T∩Ec)≤m*(E)+m*(T)≤m*(T)

從而m*T=m*(T∩E)+m*(T∩Ec)，即E為可測集。

設計思路二引導學生通過類比數(shù)學分析中求極限的方法之一：兩邊夾定理，那么判斷集合可測是否有類似的方法呢？

探索過程 類似求極限的兩邊夾定理，需要找到兩個合適的可測集，使得點集E包含在中間，而且兩端可測集的測度要相等。在不斷的分組探討中，學生在利用外測度單調(diào)性的推理過程中發(fā)現(xiàn)，可以將兩端的可測集修改為兩個可測集列，即存在兩列可測集{Fn},{Gn},使得Fn?E?Gn且m(Gn-Fn)→0(n→∞)，可得到點集E的可測性。如是最終探究出所要的結論，如下：

結論2設E?Rm，存在兩列可測集{Fn},{Gn},使得Fn?E?Gn且m(Gn-Fn)→0(n→∞)，則E可測。

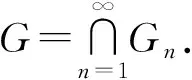
(G-E)?(Gn-E)?(Gn-Fn)，

由單調(diào)性得0≤m*(GE)≤m*(Gn-E)≤m*(Gn-Fn)=m(Gn-Fn)→0(n→∞)，

因此，m*(G-E)=0，則G-E可測，故E=G-(G-E)可測。

設計思路三引導學生通過類比數(shù)學分析探尋函數(shù)可積時，證明上和的下確界與下和的上確界相等，那么判斷集合可測是否有類似的方法呢？

與探索過程 (1)類似求曲邊梯形面積的內(nèi)填外包法，需要構造能夠覆蓋點集E的可測集測度的下確界，以及包含點集E的可測集測度的上確界；(2)根據(jù)開集和閉集是可測集，以及Rm中有界閉集和緊集的等價性，構造inf{mG:G是開集，E?G}和sup{mH:H是緊集，H?E}；(3)假設兩者相等，嘗試能否得到點集E的可測性？最終探究出所要的結論，如下：

結論3若有界集E?Rm滿足條件：

inf{mG:G是開集，E?G}=sup{mH:H是緊集，H?E}，則E是可測集。

證明記inf{mG:G是開集，E?G}=sup{mH:H是緊集，H?E}=c，由上下確界的定義，對任意的自然數(shù)n，存在開集Gn，緊集Hn，使得Hn?E?Gn,且

即存在可測集列{Hn},{Gn},使得Hn?E?Gn，且

由結論2可得E可測。

此外，還有同學直接通過開集和閉集的可測性，也能直接利用開集或閉集直接來刻畫可測集，得到下面充要條件：

結論4設E?Rm，E是可測集?對任意ε>0，存在開集G，使得G?E且m*(G-E)<ε。

結論5設E?Rm，E是可測集?對任意ε>0，存在閉集F，使得F?E且m*(E-F)<ε。

2 解題中的應用

通過總結歸類的方式進行啟發(fā)式探討，讓學生自主總結判斷集合可測的一些判定條件，老師緊接著給出幾道練習題，讓大家合理應用判定條件來解題，最終讓學生真正領悟并掌握這些重要的結論。

例1設A1,A2?Rn,A1?A2，A1是可測集且有m(A1)=m*(A2)<∞，試證明A2是可測集。

證明由于A1是可測集，根據(jù)Caratheodory條件，取T=A2，則

由于m(A1)=m*(A2)<∞，因此m*(A2-A1)=0。則由結論1知A2-A1可測。所以，A2=(A2-A1)∪A1是可測集。

例2設E?Rm，對任意ε>0，存在開集G1,G2，使得E?G1,Ec?G2,m(G1∩G2)<ε，則E是可測集。

證明對任意n∈，存在開集An,Bn，使得

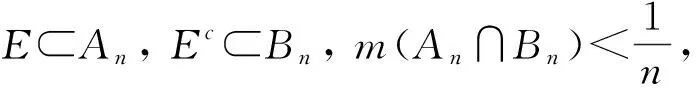
由結論2得E可測。

注本題的解答合理運用了判定條件2，事實上，此題反過來也是成立的，也就是說，這也是一個充要條件。

3 結語

在本節(jié)課的教學中，充分調(diào)動了學生的積極性，使他們在老師的適當引導下積極參與探索，也成功融入了翻轉課堂的教學理念，讓學生成為課堂的主體，在整個過程中，也體現(xiàn)著數(shù)學核心素養(yǎng)。通過問題驅(qū)動，培養(yǎng)學生對數(shù)學的熱愛，讓學生體驗數(shù)學之美，激發(fā)他們的求知欲，也可以增強學生提出問題的意識，提升數(shù)學抽象、批判性思維的能力。