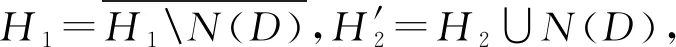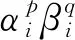帶邊Seifert流形的H′-分解的結構

雷逢春， 徐 妍

(大連理工大學 數學科學學院，遼寧 大連 116024)

每個緊致連通可定向三維流形M都有Heegaard分解， 即存在M中一個可定向閉曲面F，F把M切成兩個壓縮體C1和C2，C1∩C2=?+C1=?+C2=F，C1∪FC2=M.最近， 可以證明， 任意緊致連通可定向三維流形M都有H′-分解，即存在M中一個緊致連通可定向曲面F，F把M切成兩個柄體H1和H2，H1∩H2=F，H1∪FH2=M.顯見，當M是閉三維流形時，Heegaard分解與H′-分解是一致的；當M是帶邊三維流形時，Heegaard分解與H′-分解是不同的分解，文[1]給出了柄體的H′-分解的特征描述.

Seifert流形是一類重要的三維流形， 其拓撲分類已完全清楚， 對其Heegaard分解的結構也有著很透徹的了解.如在文[2]中，J. Schultens給出了帶邊Seifert 流形的特征描述, 在文[3]中, J. Schultens給出了緊致可定向曲面×S1的Heegaard分解的分類，在文[4]中，Y.Moriah和J.Schultens證明了Seifert流形的不可約的Heegaard分解或是豎直的，或是水平的.

本文研究了帶邊Seifert流形的H′-分解的結構，主要結果給出這類流形的H′-分解的特征描述.本文第2節介紹了必要的預備知識和若干引理，第3節給出主要定理和證明.

1 預備知識

本文中涉及的三維流形和曲面都默認是緊致可定向的，未詳細定義的概念都是標準的，可參見文[5]或文[6].

設D為平面上的單位圓盤，D上的點用極坐標(θ,r)表示.設p和q為一對互素的整數，p>0.顯然，商空間D×I/(θ,r,0)～(θ+2πq/p,r,1)為一個實心環(≌D×S1),記作T(p,q).記商映射為ρ:D×I→T(p,q).對于圓心O∈D,e=ρ({O}×I)是T(p,q)中的一條簡單閉曲線；對于x=(θ,r)∈D{O},ρ((θ,r,0)×I)∪ρ((θ+2πq/p,r,0)×I)∪…∪ρ((θ+2πq(p-1)/p,r,0)×I)是T(p,q)中的由p條簡單弧依次首尾相連構成一條簡單閉曲線.這些簡單閉曲線均稱為是T(p,q)的纖維.稱T(p,q)為一個標準的(p,q)-型纖維化實心環.若p>1,稱e為T(p,q)的奇異纖維，稱T(p,q)的非e纖維為正則纖維.當p=1時，T(1,q)的每個纖維均為正則纖維.

容易看到，T(p,q)是它的所有纖維的無交并.

設T1、T2是兩個標準的纖維化實心環(型可能不同)，h:T1→T2為一個同胚.若h把T1的每個纖維送到T2的纖維，則稱h為保纖同胚.此時，也稱T1和T2是同構的.

定義1設M是一個3-流形.若M可以分解成一族互不相交的簡單閉曲線(稱每個這樣的簡單閉曲線為一個纖維)的無交并，使得每個纖維在M中有一個管狀鄰域保纖同胚于一個標準的纖維化實心環，則稱M為一個Seifert流形.

將Seifert流形M的每個纖維粘成一點所得的商空間是一個曲面B，稱之為M的底空間，對應的商映射記為π:M→B.M的每個奇異纖維在底空間B上的像點稱為奇點.顯然，每個奇點都是B的孤立點，即它在B上有一個鄰域，其中，只有其本身是奇點.若M是緊致的，則M只有有限多個奇異纖維，這時B只有有限多個奇點，且落在B的內部.

令S為M所有奇異纖維之并，s=π(S)為所有奇點之集，則π|MS:MS→Bs是曲面Bs上的一個S1-叢.由此可知，緊致可定向的Seifert流形M的每個邊界分支均為環面.詳可參見文[7].

定義2設M為一個緊致Seifert流形，F為M中一個真嵌入曲面.若F為M中若干正則纖維之并，則稱F是一個豎直曲面；若F與M的所有纖維均橫截相交，則稱F是一個水平曲面.

定義3設M1,M2為兩個緊致連通可定向三維流形，Fi??Mi是一個緊致連通曲面，i=1,2，h:F1→F2為一個同胚.令

M=M1∪M2/x～h(x),?x∈F1,

稱M為M1和M2沿F1和F2的一個融合,記作M1∪hM2,或M1∪FM2,其中，F=F1=F2.當M1和M2都是壓縮體,且?+M1=F=?+M2,稱M1∪FM2為M的一個Heegaard分解;當M1和M2都是柄體,稱M1∪FM2為M的一個H′-分解.

定義4設N為m-流形M中一個嵌入的n-流形，n

從纖維叢理論可知，若緊致連通可定向3-流形M是閉曲面F上的I-叢，ρ為其伴隨映射，則?M是F上的?I-叢，ρ|?M:?M→F是一個2重覆蓋映射.M由ρ|?M完全決定.若|?M|=2,則M≌F×I；若|?M|=1,則稱M為一個扭的I-叢，此時，F是不可定向的曲面.

例

(1)設F為一個曲面，F×I、F×S1都是纖維叢,也稱這樣的纖維叢為積叢或平凡叢.

(2)設M為一個莫比烏斯帶，C為M上的中位線，則M是C上的I-叢.M為非平凡叢，通常稱這樣的叢為扭的I-叢.一般地，從Pn中除去一個開的n-球體所得的流形是Pn-1上扭的I-叢.

三維流形中的不可壓縮曲面的定義、邊界不可壓縮的曲面的定義可參見文[5]或文[6].若三維流形M中的一個真嵌入曲面F是不可壓縮的、邊界不可壓縮的，且F不平行于?M的子曲面，則稱F是M中的一個本質曲面.特別地，若F是一個2-球面，且F不界定M中一個實心球，則稱F為一個本質球面.若M包含一個本質球面，則稱M是可約的，否則，稱M是不可約的.

引理1設M=M1∪FM2是兩不可約三維流形M1和M2沿F的融合.若F在M1和M2中均是不可壓縮的，則M是不可約的.

引理1的證明可參考文[8].下面引理出自文[7]，將在第3節中用到.

引理2設M為一個緊致連通不可約可定向的Seifert流形.則M中的每個本質曲面可以同痕于一個水平曲面或一個豎直曲面.

2 主要定理及證明

下面給出緊致連通可定向帶邊Seifert流形的H′-分解的特征描述.

定理1設M為一個緊致連通可定向帶邊流形，H1∪FH2是M的一個H′-分解.假設F在H1和H2中均是不可壓縮的.則M是一個Seifert流形當且僅當M為下列兩種情形之一：

(1)H1和H2均為實心環體，且曲面F是?Hi上的豎直平環，i=1,2;或

(2)對于i=1,2，Hi是Si上的扭I-叢，ρi為其伴隨映射，ρi|F:F→Si是一個2重覆蓋映射,且粘合映射h:F→F是周期自同胚.

證首先證明必要性.由假設和引理1可知，F在M中是不可壓縮的，M是不可約的.M是一個緊致帶邊可定向Seifert流形，故?M的每個分支都是環面.由引理2，F同痕于M中一個水平曲面或豎直曲面.下面就這兩種情形分別討論.

情形1：F同痕于一個豎直曲面.

不妨設F就是一個豎直曲面.F為M的若干正則纖維的無交并，故F是一個S1-叢，從而F或是一個平環，或是一個環面，或是一個Klein瓶.因F是帶邊曲面，F只能是一個平環.又?M的每個分支都是環面，故?F所在的?Hi的分支均為環面，i=1,2.因Hi是個柄體，從而Hi是一個實心環體，且F是?Hi上的豎直平環，i=1,2.

情形2：F同痕于一個水平曲面.

不妨設F就是一個水平曲面.設π:M→B為M到底空間B的商映射.此時F到底空間B的投射πF:F→B是一個n-重的分歧覆蓋，使得對M的每個(p,q)-型纖維化實心環中的奇異纖維C，π(C)是個重數為p的分歧點，p整除n.

因πF:F→B是滿射，F與M所有纖維都相交.M的纖維均與F橫截相交，從每個纖維的標準化鄰域與F相交的每個分支的局部情況可知沿F切開M所得流形MF是一個I-叢.

F分離M為柄體H1和H2.對于i=1,2,每個Hi是其中的嵌入曲面Si上非平凡的I-叢,否則，Hi=Si×I,F=Si×{0},Si×{1}??M,矛盾.這樣，每個Hi是Si上的扭I-叢,ρi為其伴隨映射，ρi|F:F→Si是一個2重覆蓋映射,i=1,2.由πF:F→B是一個n-重的分歧覆蓋可知，粘合映射h:F→F是周期為n的自同胚.

充分性顯然.定理得證.