因勢而『為』巧整合 精準采『點』深思辨
——以《分數的初步認識》單元統整為例

文|陳飛 莊旦丹

錯例：把2個相同的面包平均分給3位同學，每位同學分到這些面包的（）。

這一類型是學生熟悉得不能再熟悉，卻又“反復受傷”的題目，甚至到了畢業考試，正確率仍不容樂觀。筆者曾對本校五六年級的學生做過調查，錯誤率分別高達58.6%和32.9%，在訪談中筆者還發現兩個現象：一是找不準單位“1”。但當教師在“這些面包”下面劃出橫線，標上單位“1”時，有超過25%的學生發現了自己的問題，并能迅速答對。二是低階思維。回答正確的部分學生，機械記憶教師傳授的“秘訣”：有單位名稱的是把數量分一分，沒有單位名稱的是把單位“1”平均分。那么，怎樣從學生的認知水平和思維特征出發，合理、有序地設計立體式的教學活動，在三年級初識分數時上好“種子課”呢？筆者嘗試從以下幾個方面出發，抓住核心本質，探究深度學習。

一、為“診”而測，找準起點

前測目的：了解學生對于分數含義以及大小比較的認知程度和表征能力。

前測對象：三年級全體學生272名。

前測方式：無提示筆試+后期訪談。

前測題目：

①把1個蘋果平均分成2份，每份是（）個。

②如果把每個圖形看成整體“1”，你能用分數表示涂色部分嗎（圖略）？

從前測中我們可以看出：

1.分數表征，存在欠缺。

第①題中，有超過半數的學生寫出了正確答案，其中有個班能用“個”符號表征結果的約占全部人數的13%，另一個班中表示“個”的人數有所下降，用半個表示的人較多，說明學生對整數以外的數有一定的了解。從第④題看出，學生具備了畫圖表征的經驗，但在“平均分”和“涂出一份”這兩個點上，學生錯誤率較高，說明學生對于的圖像表征理解不完整，還存在著一定欠缺。

2.分數含義，理解模糊。

學生對分數的書寫形式有了初步的感知，有個班對于總份數理解尚可，但顛倒了總份數與所取份數的位置；另一個班不僅有同樣的錯誤，而且對于總份數的理解還存在偏差，準確率不到10%。由此可見，學生不能準確把握分數中總份數與所取份數這兩個量與分子、分母之間的聯系，對于分數所表示的含義是模糊的，在分數本質理解上很不到位。

3.分數比較，粗淺模仿。

純數字化的比大小較為抽象，學生還沒有這方面的表象。在訪談中發現，同分母分數大小的比較學生建立在最初的整數大小比較的模式上，這種遷移僅僅停留在模仿層面，對同分子異分母分數大小的比較很陌生。

二、為“源”而理，聚合散點

要跨越以上幾點“障礙”，重要的是整體理解教學內容的內在關聯性，再加以分解，逐步把目標具體化。為此，筆者從橫向和縱向兩個方面出發，做了深入的解讀分析，以此追根溯源，避免短視行為。

1.橫向梳理，解讀單元教材內容。

通過橫向梳理教材內容，我們可以發現，分數的初步認識是在學生掌握整數加減法、除法的意義等基礎上學習的。分數和自然數一樣，是一種有大小的數，可以表示具體量的大小，也可以表示兩個量之間的倍比關系。從數的疊加到數的均分是數概念的一次擴充，它是后續分數的意義和小數初步認識的基礎。

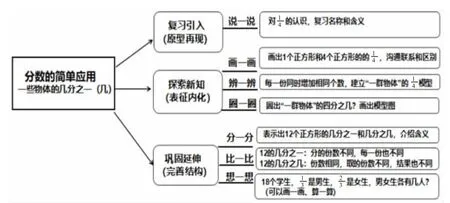
三年級上冊“分數的初步認識”是學生第一次接觸分數，單元知識結構為：分數的初步認識（認識幾分之一，幾分之一比大小，認識幾分之幾，同分母分數比大小）；分數的簡單計算（分數加減法，1減幾分之幾）；分數的簡單應用（把一些物體看成整體，解決問題，整理和復習）。

由于學生第一次接觸較為抽象的分數，所以教材在內容的編排上有以下幾個特點：（1）教學內容，步子略小。從分數的初步認識——分數的簡單計算——分數的簡單應用，在難度上進行了分散，用分數的計算緩沖了“一個物體”到“一些物體”帶給學生的認知負擔。但從另一個角度而言，這樣的小步子教學略顯“碎片化”，就分數含義揭示的一般性而言，缺乏整體化的觀察和對比，不利于學生抽象思維的發展。（2）大小比較，植入過早。同分子（母）分數的大小比較，緊跟在分數的認識之后。多數學生發現規律后，就會直接進行應用，導致分數大小比較過早形式化，對于分數含義的鞏固不利。（3）畫圖表征，比重不足。在學習解決問題之前，教材基本以直接給出直觀圖為主，學生的畫圖能力沒有得到足夠的重視，這也使學生在后面的學習中出現不會表征或表征單一，以及題意和圖示不相對應等現象，對于解決問題造成一定的困難。

2.縱向比較，把握教材前后脈絡。

“只見樹木不見森林”的教學，難于從整體上把握教材結構。小學階段有關“分數”的教學內容主要分布在哪些年級？每節課的主線是什么？承載的目標是什么？前后又有哪些關聯？筆者對教材進行了縱向的比較，從比較中可以發現，三年級上冊的“分數的初步認識”直接影響著五年級下冊“分數的意義和性質”的教學；“分數的簡單計算”為五年級下冊“分數的加法和減法”算理的理解和算法的掌握積累豐富的計算經驗；“分數的簡單應用”是六年級上冊分數乘除法的雛形。由此可見，三年級中有關分數的知識點，對后續的學習起著重要的奠基作用。

三、為“效”而整，撬動支點

分數概念的建構是一個螺旋上升的過程。三年級學生認知經驗是有局限的，認知方式是感性的。此時學生只要結合具體情境進行平均分和分數之間的自如轉化，并感受到分數是一個由三個部分組成的整體來表示“平均分不到1的結果的大小”，目標即達成。因此，學生只有撬動“行為”和“符號”之間的一一對應關系這一支點，才能從直觀經驗建構概念深入到充分關注分數的本質內涵。

1.聚焦目標，讓整合教學更有“理”。

綜合前測解讀和教材分析，筆者認為在教學中應該做到以下三點：（1）增加有關分數“量”的學習，并加強在“量”的聯系對比中過渡到“率”，理解分數的含義。（2）通過豐富的操作活動，從面積模型、數線模型過渡到數量的關系，進一步感知分數的本質特征。（3）引導學生在可視化的表征中理解掌握解決分數問題的多樣化策略。為此，筆者對本單元的內容做了以下的重組和調整——認識幾分之一和幾分之幾；練習課；把一些物體看成一個群體；解決問題；練習課；分數比大小；分數的計算；練習課；整理和復習。

2.分層推進，讓知識銜接更有“利”。

立足“分數的初步認識”中分數的含義、應用與計算三個知識內容，將本單元學習課時進行重組、調整。（1）把“認識幾分之一”和“認識幾分之幾”4個例題合并成1課時，讓學生從整體的角度更好地感知分數的含義，明確總份數、所取份數和分子、分母的一一對應關系。（2）將“把一些物體看成一個群體”、“解決問題”2個例題進行前置，在原有教學目標的基礎上，整合“分數的簡單運用”中“以多當一”的內容，讓學生在理解“幾分之一”的基礎上，從單個數量的幾分之一走向多個數量的幾分之一模型建構，并趁熱打鐵用多種表征解決分數的相關問題。（3）將“分數比大小”和“分數計算”2課時延至第三階段，引導學生從“一個物體”和“一些物體”兩個維度出發去思考、去表征，讓分數的大小比較在具象和抽象之間來回溝通，更加豐富、更加立體，從而進一步鞏固分數的含義，明確行為和符號的對應關系。另外，每一大塊知識點之后都設置了相應的練習課，對整合的內容進行及時鞏固和拓展。

3.多元表征，讓探究生長更有“力”。

筆者從概念表征的視角出發，對本單元主要新授課的思路進行架構。通過“原型再現”、“表征內化”、“完善結構”三個主要步驟，完整表征間的轉化和互譯，順應兒童學習心理的發展，引導學生逐步認識分數，讓學習充滿生長的力量。

（1）尋分數產生之源，循序漸進。

以“分紙”切入，架構除法和分數之間的聯系；用“量”呈現，感受分數產生的必要性；以“量”導“率”，畫物體或圖形的個——折幾分之一個——涂幾分之幾個——提煉分數含義——構建分數模型，感受計數單位的累計。

（2）探分數結構之本，抽象建模。

“以一當一”延伸至“以多當一”，引發認知沖突，溝通聯系區別；借助圖形，呈現“整體”的不同類型，構建分數模型，探究分數結構的本質；任務驅動，利用《學習單》表示一些物體的幾分之一和幾分之幾，摒棄一問一答式的教學方式；交流探究，在對比中體會變與不變。

（3）融分數理法之美，策略共生。

如何讓圖示會“說話”，最重要的是“會悟”。教材中的分數比較是直接給出直觀圖，降低了難度。整合后的教學引導學生從“一個物體”和“一些物體”兩個層面出發進行思考，探究過程中需要悟出三個層次：一是統一標準。在同分母分數比較大小時，學生出現了分子大的分數反而小的情況，通過觀察，學生發現錯例中所取的標準不一，的正方形圖大，的正方形圖反而小。通過對比，學生明白必須統一標準，即同一個物體或同樣多的一些物體，否則就不公平。二是確定數量。在幾分之一的大小比較（和）時，選擇“一些物體”表征有一定難度，學生發現統一標準（數量為5個）后，無法表示。通過討論發現，只統一標準還不夠，數量的確定還大有講究，進一步引導學生需要找兩個分母的公倍數（分母相乘）。三是等值“替身”。拓展部分給出分子和分母都不同的兩個分數，引導學生明白除了畫圖，還可以尋找“替身”即等值分數比較更為簡單，實現策略的多樣化和優化。在三個“悟”中，進一步鞏固分數的含義，也讓學生感悟到分數的大小比較就是在比相同計數單位的個數。

4.題盡其用，讓知識聯結更有“底”。

單元重組并不一定是單元內所有知識的一個整合，也可以是單元內習題的整合、內容的補充、知識的拓展等，關鍵是要具備單元整合的意識。

（1）以小見大，提升高度。

“分數的初步認識”第1課時跟進練習：你能表示出下面這條線段的幾分之一或幾分之幾嗎？

（線段長10厘米，事先不告訴學生長度）

在揭示分數的各部分名稱、初步認識分數的含義后，學生已經對“平均分”深有感觸。所以碰到這道題時，學生會先進行測量，然后根據經驗平均分成若干份（2、5、10份），并選取其中的1份和幾份用分數表示。教師給予肯定并及時追問：為什么同樣一根線段，大家所表示的分數卻不一樣呢？討論后引導學生發現，在0-1之間有無數個分數，并用數線的形式進行展示，讓學生感悟分數就是把“1”進行不斷均分產生的。

（2）動態分步，拓寬廣度。

“分數的初步認識”第2課時跟進練習：①出示圖（a），估一估灰色小正方形是整個大正方形的幾分之幾？你有什么方法驗證？②出示圖（b），你能用分數表示陰影部分嗎？③出示圖（c），現在你還能想到哪些分數呢？

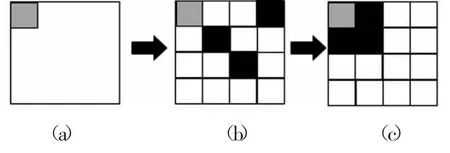
在本題中，題①結合估算培養學生的空間觀念，并鼓勵學生用折一折、量一量、分一分等方法進行驗證，感受策略的多樣化；題②的陰影部分是離散的，讓學生感受分數單位的累計產生新的分數；題③的陰影部分通過移動，讓學生感知可以從不同角度進行觀察，滲透了分數的基本性質。通過動態分步呈現習題，把看似比較簡單的內容進行合理拓展，使學生的思維逐漸變得深刻、靈活。

（3）內容延伸，挖掘深度。

“分數的大小比較”跟進練習：

先出示題①，引發學生認知沖突，質疑為什么同樣的兩個分數，大小會不一樣呢？引導學生畫圖驗證。隨后馬上跟進題②，從部分推理整體，考查學生的逆向思考能力。通過題組對比練習拓展延伸，讓學生明白當單位“1”的量不同時，得到的分數可能相同也可能不同，為以后分數的學習埋下伏筆。

單元重組教學不是教學內容簡單的合并、增加與調換，教師“心中需有一盤顧全大局的棋”才能高瞻遠矚；學生“腦中需有一張思維導航的圖”才能觸類旁通。只有抓住核心、觸及本質的統整，才能讓深度學習真正發生。