多角度探究離心率問題

何艷麗

摘 要：離心率又叫偏心率，用來描述行星運行軌道形狀，解釋為形狀從圓形偏離了多少，是天體計算中定義軌道形狀的重要參數。圓錐曲線中的離心率問題綜合性比較強，又靈活多變，能很好的考查學生對圓錐曲線定義及相關知識熟練掌握的程度，以及計算的靈活運用的能力，能夠很好的考查圓錐曲線的知識，下面就從多角度研究焦點三角形中的離心率問題。

關鍵詞：離心率;圓錐曲線定義;直角三角形

焦點三角形為直角三角形時，分為兩種類型，一種是一個焦點與另一焦點及橢圓上點的張角為90°。另一種是橢圓上點與兩焦點的張角為90°;利用直角幾何關系體現邊角之間的關系，向雙曲線定義靠攏，得出基本量關系，利用離心率基本公式求得離心率。

例1：設橢圓（a>0，b>0）的左、右焦點分別為F1，F2，P為C上的點，PF1⊥F1F2，∠F1F2P=30°，則C的離心率為

A. B. C. D.

正確答案：D

方法一：在Rt△ABC中，|F1F2|=2c，∠F1F2P=30°，則|PF1|=，|PF2|=，

由橢圓定義，|PF1|+|PF2|==2a，所以

精簡過程：設|PF1|=1，由已知|F1F2|=，|PF2|=2，則。

方法二：在Rt△ABC中，|PF1|=，

則b2=2ac，又b2=a2-c2，所以a2-c2=2ac，所以e2+2e-=0.

解得e=。

這種直角三角形的離心率問題比較簡單，可直接找到三邊關系，利用橢圓、雙曲線基本定義，直接解決問題。

例2：已知F1，F2分別是橢圓（a>0，b>0）的左、右焦點，若橢圓上存在點P使得PF1⊥PF2，則該橢圓離心率的取值范圍是

A.[，1） B.[，1）

C.（0，] D.（0，]

正確答案：B

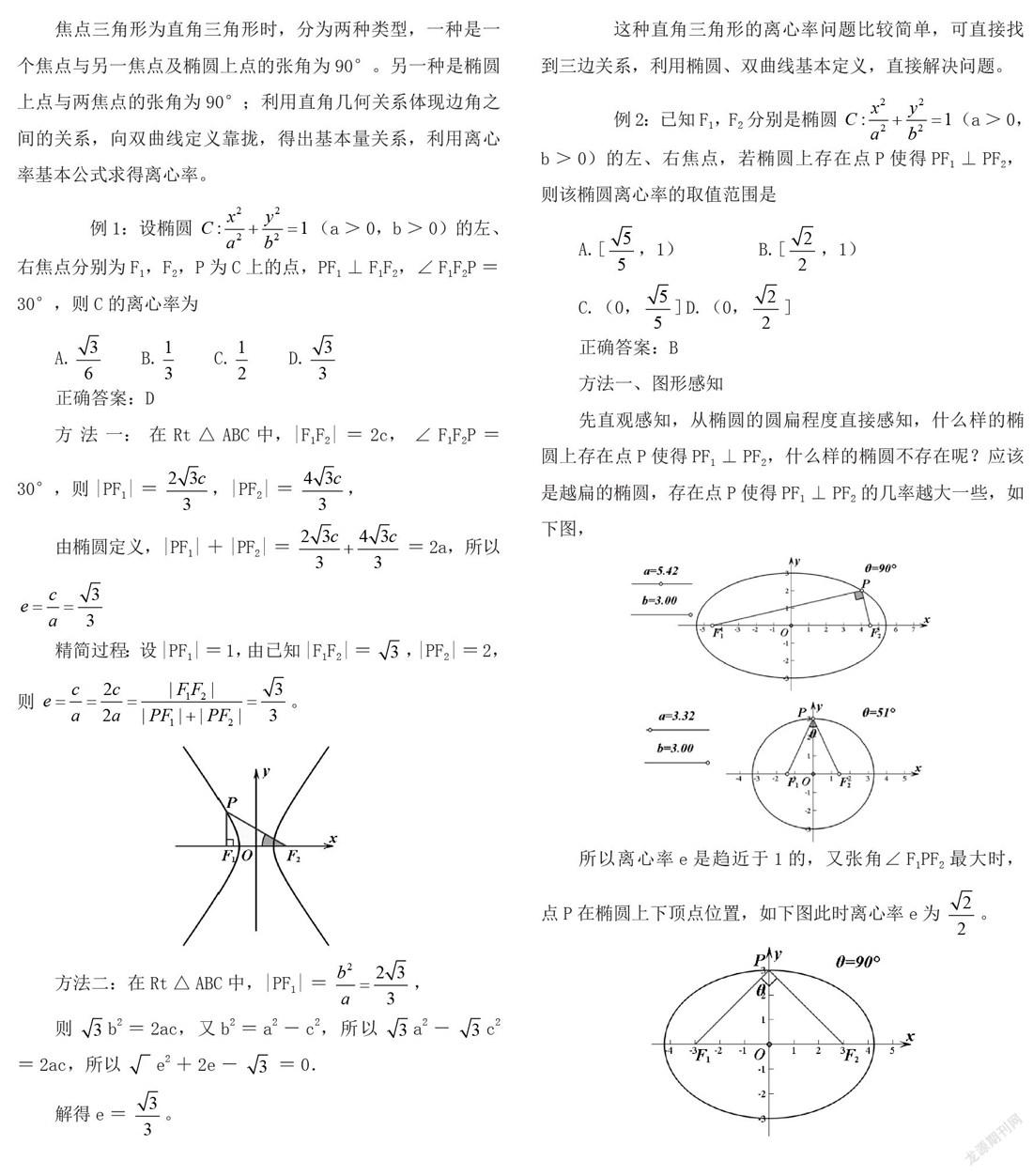
方法一、圖形感知

先直觀感知，從橢圓的圓扁程度直接感知，什么樣的橢圓上存在點P使得PF1⊥PF2，什么樣的橢圓不存在呢？應該是越扁的橢圓，存在點P使得PF1⊥PF2的幾率越大一些，如下圖，

所以離心率e是趨近于1的，又張角∠F1PF2最大時，點P在橢圓上下頂點位置，如下圖此時離心率e為。

方法二、幾何法1設|PF1|=r1，|PF2|=r2，|F1F2|=2c，

則又，

所以4c2≥，即2c2≥a2，即e2≥，所以≤e<1。

方法三、利用焦點三角形面積

設|PF1|=r1，|PF2|=r2，△PF1F2的面積S=r1r2==b2，所以r1r2=2b2≤==2a2，即b2≤a2，所以a2-c2≤c2，a2≤2c2，e2≥，所以≤e<1。

方法四、坐標法

理解條件PF1⊥PF2，動點P在以F1F2為直徑的圓上，又點P在橢圓上，所以P為圓和橢圓的交點，通過坐標法解決。

聯立消y得，

因為0≤x2≤a2，0≤≤a2，解得≤e<1。

方法五、幾何法2

由上面的方法二可知，P為圓和橢圓的交點，觀察下面的圖形。

發現如果保證圓與橢圓有焦點，b≤c，

兩邊平方，b2≤c2，即a2-c2≤c2，a2≤2c2，所以≤e<1。

方法六、用橢圓定義及正弦定理

設∠PF1F2=α，∠PF2F1=β，由已知α+β=90°，α∈（0，）。

因為α∈（0，），所以α+∈（，），所以sin（α+）∈（1，]，e∈[，1）。

利用焦點三角形求解離心率問題中，三角形設置多為特殊的三角形，通過特殊角或者邊的關系，利用正余弦定理，得出基本量的關系，從而到達離心率的求解。對于垂直關系PF1⊥PF2的理解還可以有很多角度，比如：向量點積為零，斜率互為負倒數等，每種解法都進行嘗試，拓展學生視野，在實踐中對解法進行衡量對比，為以后的考試積累經驗，形成正確的數學感覺，理解解析幾何的本質，形引路，數計算，數形深度融合。

參考文獻

[1]李瑩琪.橢圓離心率求解方法探究[J].科學咨詢（科技·管理），2019（02）：165-166。

[2]申楠.判別式法在高中數學中的應用[J].納稅，2017（23）：174.