Sturm-Liouville 算子的一維奇異擾動的逆特征值問題

吳雪雯

(西北工業(yè)大學(xué)數(shù)學(xué)與統(tǒng)計學(xué)院， 陜西 西安710072)

1 引言

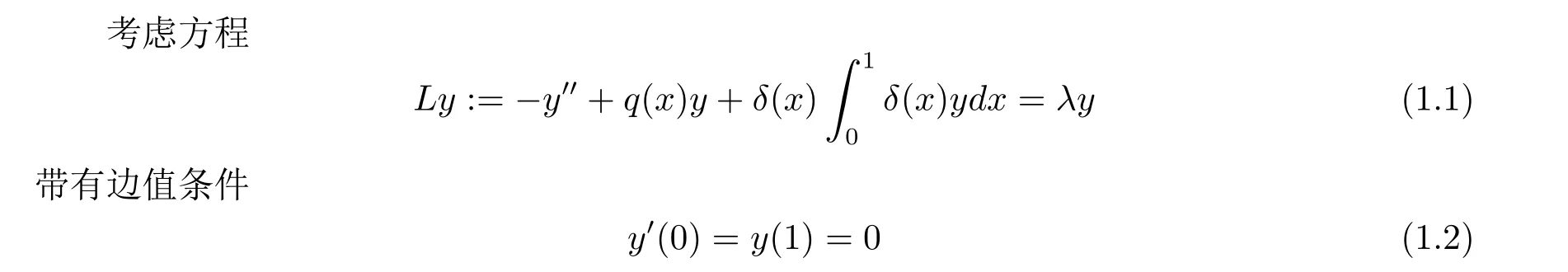
其中q(x)∈L2(0，1)，δ(x) 是狄拉克函數(shù). 這里算子L是自伴的并且是Sturm-Liouville 算子L0y:=-y′′+q(x)y帶有邊值條件(1.2) 的一個一維奇異擾動. 由文獻[1] 知， 算子L0在L2(0，1) 上是自伴的且下半有界， 它的譜由特征值組成.

本文的目的是通過運用Sturm-Liouville 算子的逆譜理論(見文獻[1])， 由算子L0及L的譜重構(gòu)(1.1) 中的勢函數(shù)q(x). 然而， 方程(1.1) 的初值問題無法直接解出. 結(jié)合文獻[2] 中的方法， 我們研究的逆問題可以由Sturm-Liouville 算子的逆譜理論有效地解決.

Sturm-Liouville 算子的一維擾動的譜問題[2-5]中已有所研究. 關(guān)于逆問題， 擾動項是屬于L2(0，1) 中函數(shù)的算子已被考慮過， 例如文獻[6， 7]. 由文獻[2]， 我們知道擾動項的函數(shù)可以為奇異函數(shù). 我們的文章考慮的算子L0的擾動項是δ(x). 通過運用文獻[2] 中的方法， 我們得到了算子L的特征值函數(shù)， 這為我們之后考慮的逆問題提供了一個必要的準(zhǔn)備. 關(guān)于其它的Sturm-Liouville 算子的一維擾動的逆問題， 見文獻[8， 9].

本文的主要結(jié)論是， 已知算子L0的譜為{λn}∞n=0， 如果一列實數(shù)列{μn}∞n=0滿足一個交替性質(zhì)及漸近式， 則存在勢函數(shù)q(x) 使得算子L的譜是{μn}∞n=0. 下一節(jié)我們將陳述這個主要結(jié)論及證明， 并且給出重構(gòu)q(x) 的具體算法.

2 預(yù)備知識

首先我們提及一些需要用到的預(yù)備知識， 參見文獻[2， P8-10].

引入關(guān)于算子L0的如下的線性賦范空間H±1(L0). 定義H+1(L) 是D(L1/2) 以

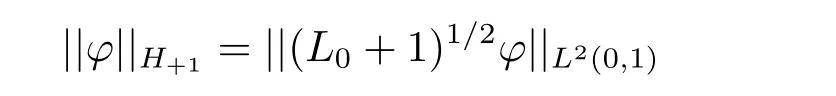
為范數(shù)的線性賦范空間， 易知，H+1(L0) 是完備的;H-1(L) 是L2(0，1) 以

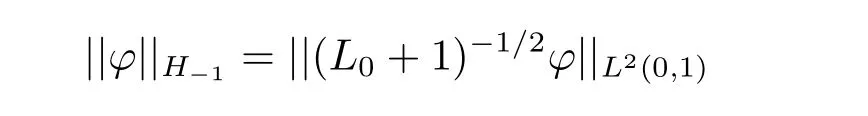
3 主要結(jié)論及其證明