G- 布朗運動指數泛函的矩估計

胡鑫宇， 閆理坦， 郭夢凡

(1. 東華大學理學院統計系，上海201620)

(2. 中國工商銀行上海分行，上海200120)

1 引言

在快速發展的金融市場， 金融衍生品的定價問題一直以來都是人們關注的焦點， 其中亞式期權作為股票期權衍生的一種新式期權， 其特殊性在于它是通過相關證券在合同期間某段時間內的平均價格來決定回報， 這就既減少了合同期內價格浮動對期權定價的影響， 同時也能較為準確地反映資產價格的浮動趨勢. 在經典的Black-Scholes 期權定價模型中， 亞式期權的定價問題等價于布朗運動指數泛函的分布問題， 可以表示為以下數學形式， 若～B(t)為標準布朗運動

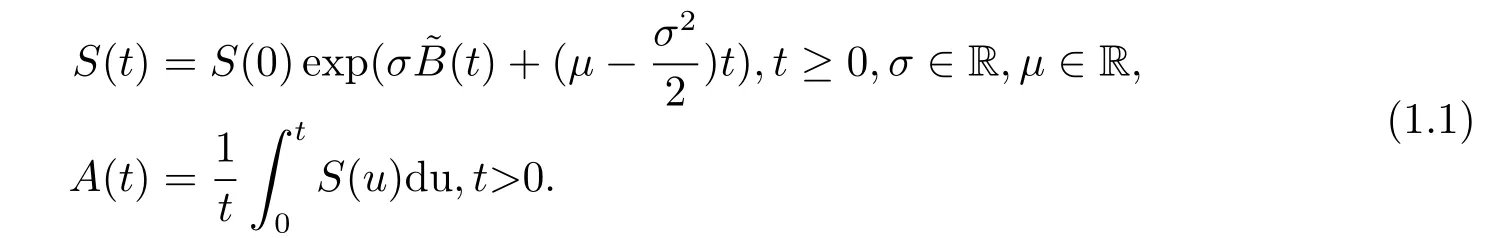
其中S(t)為定價過程，A(t)為平均定價過程.

近些年來， 眾多學者對布朗運動指數泛函的相關問題進行了廣泛研究. Marc.Yor[1]，Dufresne.Daniel[2-3] 研究了指數泛函的分布問題并將其應用于風險理論與年金問題中.Tam′as.Szabados[4-6] 利用對稱隨機游動構造出指數泛函的離散化形式， 進一步研究其矩問題.

然而Black-Scholes 定價公式本身的一些假設與現實存在差距. 比如金融資產價格服從對數正態分布， 且波動率為常數. 但實際上， 波動率可能是不確定的， 不一定是常數.G- 布朗運動的參數在一個區間內變化， 更加符合復雜多變的金融市場. 在不確定問題、風險測度和金融中的超套期保值問題的驅動下， 彭實戈[7-8] 院士提出了次線性空間的概念， 這是概率空間的一個推廣.G- 正態分布與G- 布朗運動在次線性期望理論中起著正態分布與布朗運動在線性期望中相同重要的作用.

2 預備知識

定義2.1 令Ω 為給定非空集合， H 為定義在Ω 上的由全體實值函數組成的線性空間，且滿足1∈H; 若X ∈H， 則|X|∈H; 若φ ∈Cb，Lip(Rd)，Xi ∈H，i= 1，2，···，d， 則有φ(X1，X2，···，Xd)∈H. 其中Cb，Lip(Rd)表示Rd上的全體有界Lipschitz 函數的集合. 如果定義在H 上的函數?E 滿足對任意X，Y ∈H， 有

(1) 單調性: 若X ≥Y， 那么?E[X]≥?E[Y]，

(2) 保常性: 對任意c ∈R， 有?E[c]=c，

(3) 次可加性: ?E[X+Y]≤?E[X]+ ?E[Y]，

(4) 正齊次性: 若λ ≥0， 則?E[λX]=λ?E[X]，

則稱函數?E 為次線性期望. (Ω，H，?E)為次線性期望空間， 其中H 被看作是Ω 上的隨機變量空間.

定義2.2 在次線性期望空間(Ω，H，?E)中， 隨機過程{Bt，t ≥0} ∈H 叫做G- 布朗運動， 如果滿足以下條件

3 At 的積分矩

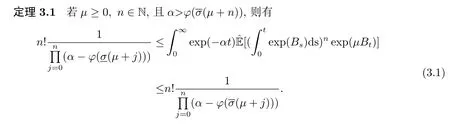
進而將公式(3.19)代入公式(3.18)可推出

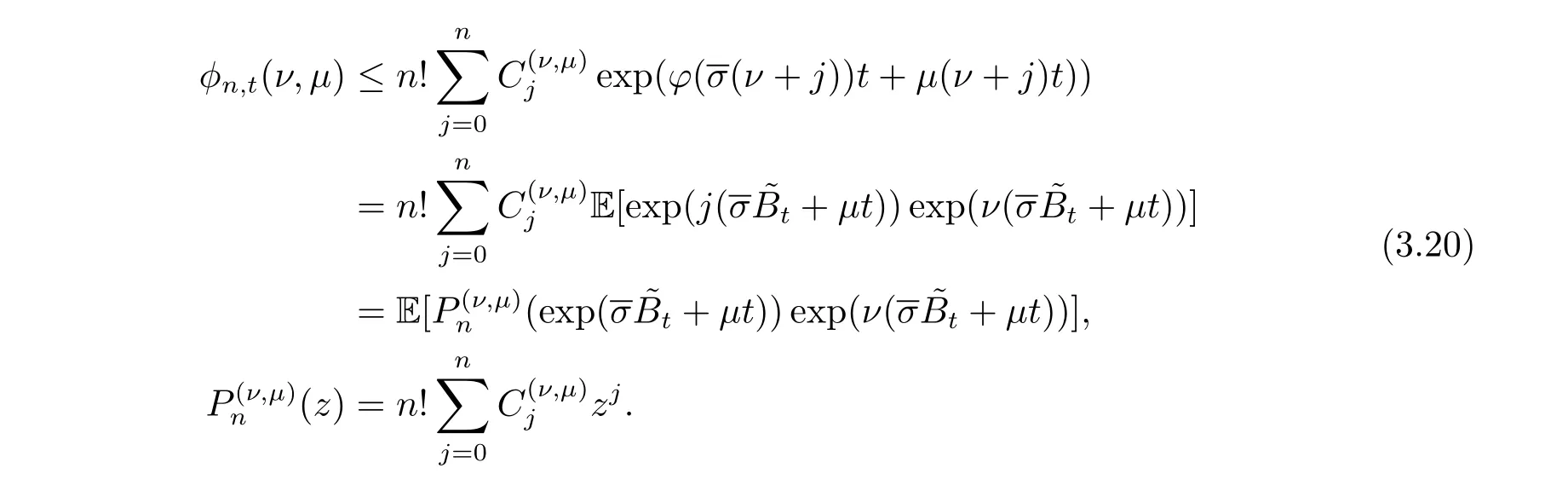
同理可得

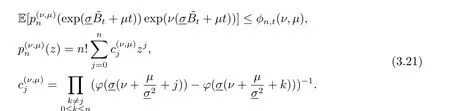
定理3.5 若λ ∈R，n ∈N， 且t ≥0， 則有進而可得

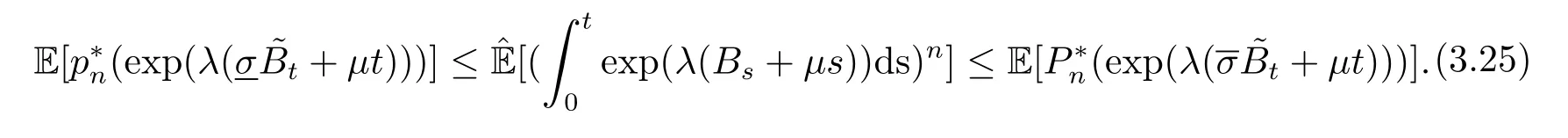
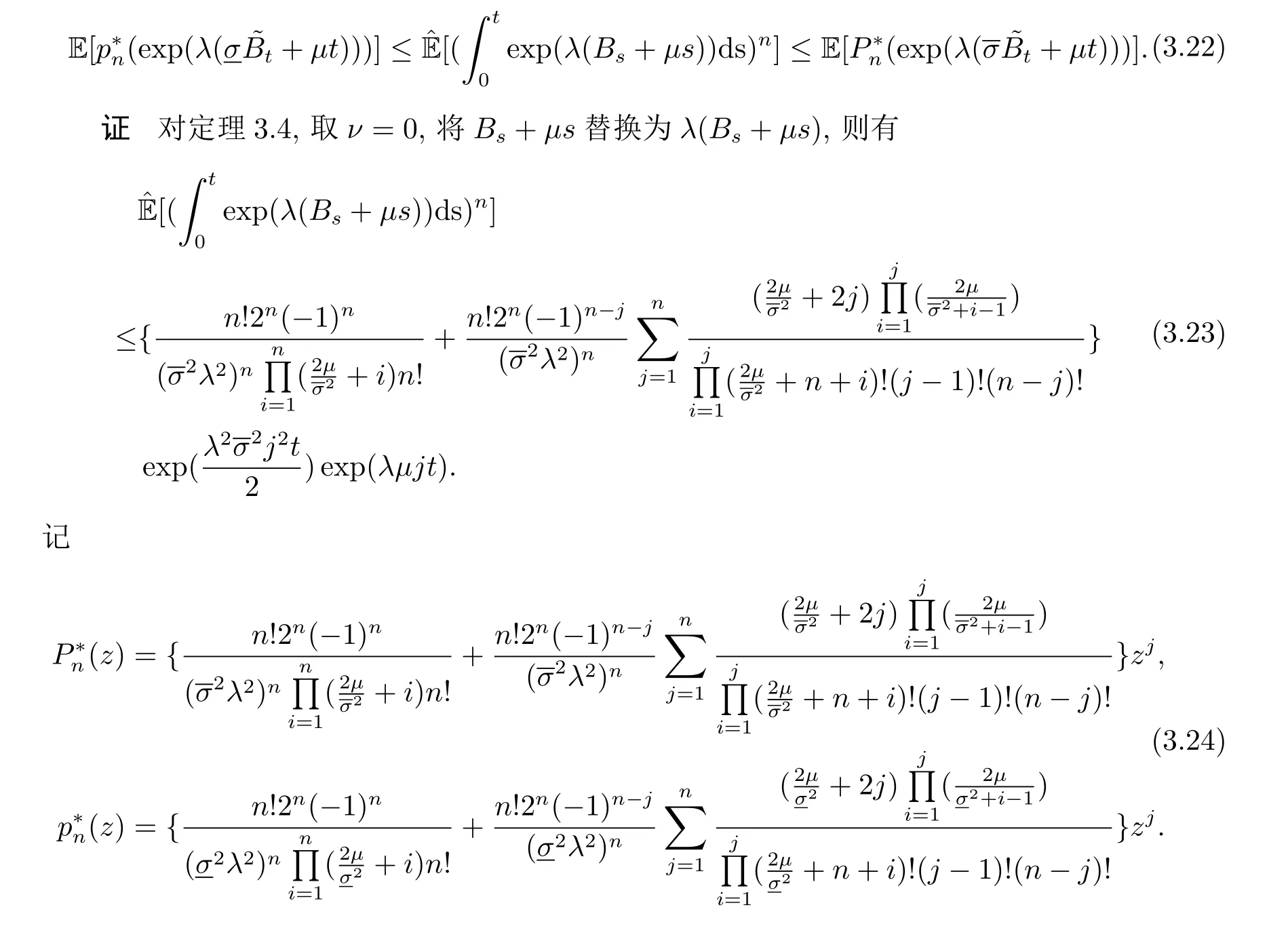
4 Y 的矩估計

參考Tam′as.Szabados[5] 提出的方法， 我們可以借助“扭曲與收縮”對稱隨機游動來定義標準布朗運動的一種近似序列， 即將單位一的步長壓縮至1/2m，m= 1，2，···， 對應完成該步長的時間被壓縮至1/22m，m=1，2，···. 接下來我們將簡述這一方法.exp(2-mXm(j) +μ2-2m). 當n →∞時，Ym，n →Ym，Ym= 2-2m(1 +ξm1+ξm1ξm2+···+ξm1ξm2···)， 且Ym滿足分布自相似性