解析游泳池中泳者“身首分離”的折射現象

邵 云

(南京曉莊學院 電子工程學院，江蘇 南京 211171)

在一個偶然的機會，筆者看到一女子在游泳池中游泳的短視頻，如圖1所示.視頻中該女子在水面上方的人臉實物與水面下方身體的虛像之間竟有如此大的“分離”，令人驚訝.筆者曾經在本刊《物點經多層平行介質界面折射成像的疊加法則及應用分析》[1]一文中對該現象進行了初步的分析，對泳者“身首”在圖1中玻璃池壁方向上的視覺分離距離進行了簡單的作圖驗證，并對其變化趨勢也進行了初步的判斷.本文則更進一步，從根本的成像位置出發，利用平面幾何與三角函數知識，定量地計算出圖1中泳者“身首”視覺分離的距離，及其隨視距、視角和深度的變化關系，并輔以圖示，籍以為讀者呈現一個更為清晰和完整的認識.

圖1 游泳池中泳者的“身首分離”折射現象

1 水下物點P經水面折射成像的虛像點位置

如圖2所示，水下h深度處一物點P發出一細束光線，在水面的入射角為i，折射角即人眼的視角為r，折射光線的反向延長線成虛像點于圖中P′點，P′位于物點P的右上方[1].姚啟鈞《光學教程》[2]給出像點P′的坐標為

圖2 來自水下物點P的某一細束折射光線成像

x′=h(n2-1)tan3i

(1)

(2)

其中水的折射率n設為4/3.

(3)

將式(3)代入式(1)、(2)即得

(4)

(5)

此即以視角r所表示的像點坐標.若令h=1 m，則根據式(4)、(5)可作出像點P′隨視角r的變化軌跡，如圖3所示.

圖3 水下h=1 m深處的物點P的虛像點P′隨視角r的變化軌跡

2 圖1中泳者“身首分離”現象的光學解析

由式(4)、(5)可見，若物點深度或者說水介質層的厚度h→0，則有x′→0,y′→0，物點與像點趨于重合.推而廣之，可以證明[3]，當光路途中某個平行介質層很薄時，它對于物點最終成像位置坐標的貢獻將可被忽略！由于圖1中的玻璃游泳池壁相對很薄，因此它對最終成像位置的貢獻近似可以忽略，即泳者水下身體的成像可近似看作水→空氣的一次折射成像，如圖4所示.

圖4 觀察者E所看到的水上物點P(人臉)和水下像點P′(人身)位置

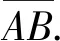
2.1 用圖4中的h、r、d來表達

根據圖4，顯然有

xA=htani

(6)

觀察者E的坐標則為

xE=htani+dsinr

(7)

yE=dcosr

(8)

鑒于P、B、E三點共線，故有比例關系：

(9)

解之得

(10)

于是，聯立式(6)—(8)、(10)，即得圖4中視覺分離的距離

(11)

再將式(3)代入式(11)，整理后便得

(12)

2.2 用圖4中的坐標xE、yE、xA來表達

當觀察者的位置(xE,yE)固定時，不難看出，圖4中的視角r、距離d均隨物點深度h的變化而變化，因此此時式(12)中的h、d、r并非彼此獨立.由圖4得

(13)

將式(13)代入式(3)可得

(14)

再聯立式(6)、(10)、(14)，整理即得

(15)

2.3 物點、觀察者位置坐標h,xE,yE均給定時的

(16)

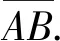
若將式(16)變形為

(17)

3 視覺分離距離的大小及變化趨勢

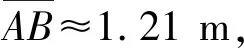
同理，當物點P的位置(即h)固定，且觀察者的距離d也固定時，通過觀察，可發現式(12)的分母是視角r的單調遞減函數，同時容易證明式(12)的分子是視角r的單調遞增函數，即有

圖5 幾個典型的觀察者位置下xB-xA隨xA的變化曲線

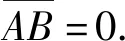
4 關于圖5中極點的計算

(18)

將圖5中的4個觀察者位置坐標：(10,1),(10,5),(10,10),(10,100)分別代入式(18)，利用Excel軟件，可算出圖5中4個極值點的橫坐標xA分別為：2.240 7 m,3.058 2 m,3.789 7 m,4.630 1 m.

4.440 6 m,1.378 5 m,0.890 0 m,0.719 5 m；

進而代入式(17)，則得對應的h值：2.013 3 m,3.987 5 m,8.796 2 m,115.039 0 m.

經檢驗，這里由式(18)算得的xA值與圖5中的極點位置吻合.

同理，利用式(15)、(17)、(18)，也可以對其他觀察者位置(xE,yE)下的情況作類似的分析.

5 觀察者位置固定時隨h的變化曲線

圖6 幾個典型的觀察者位置下xB-xA隨h的變化曲線

從曲線的形狀上看，圖6和圖5有較大的差別，其原因在于h與xA之間的函數關系式(17).盡管如此，此時的h與xA是一一單調對應的，因此圖6中的極點實質上也是圖5中的極點.

6 總結與說明

本文的結論式(12)、(15)—(18)具有普適性，它們同樣適用于其他介質情形，對于教學與科研或有參考價值.