基于GRA—BP神經網絡的固體廢棄物充填體強度預測

劉團結，趙象卓，韓永亮，李云鵬，陳 希

（1.陜西延長石油礦業有限責任公司，陜西 西安 710075；2.中煤科工集團西安研究院有限公司，陜西 西安 710075；3.遼寧工程技術大學 礦業學院，遼寧 阜新 123000；4.煤炭科學研究總院，北京 100013；5.煤炭科學技術研究院有限公司 安全分院，北京 100013）

利用固體廢棄物回填采空區可實現礦井“三下”壓煤的安全開采，提高煤炭資源采出率，并有效控制地表沉陷，同時處置固體廢棄物。煤礦充填開采可實現煤炭資源開發與生態環境保護的協調發展，現階段充填材料主要有沙子、粉煤灰、矸石、建筑垃圾、高水材料等[1]，近年來，國內外學者對充填體材料及充填技術進行了深入研究[2-6]。我國每年產生的固體廢棄物近10億t，全國固體廢棄物積累量已經超過60億t，侵占了超過20×104hm2土地[7]，無論是填埋、堆肥或是焚燒處理，都存在著不容忽視的土壤、地下水體和大氣污染的隱患，且處理成本高昂。因此，以固體廢棄物為原料加工制成不需要脫水處理的膏狀漿體，采用充填泵或重力加壓，通過管道適時輸送到井下采空區。膏體到達充填點后，在較短時間內凝固承載，有效控制地表沉陷。數量巨大的固體廢棄物保障了充填材料充足的來源，同時通過充填解決了固體廢物引起的環境污染問題，實現礦山綠色開采[1]，充填體的強度在充填工程中具有十分重要的意義，因此充填材料力學性能是取得理想充填效果的基礎。孫琦[8]分析了膏體充填開采膠結體的蠕變特性，在試驗基礎上推導了考慮時間和應力2個變量的損傷演化方程，建立了新的本構模型，推導了膠結體的三維蠕變本構方程；崔增娣[9]研究了煤矸石凝石似膏體充填材料的物理性能和力學性能，并對比研究了水泥混凝土和以煤矸石凝石似膏體充填材料為膠凝材料的混凝土的耐久性能；何榮軍[10]在粉煤灰膏體管道輸送中將最大最小蟻群算法（MMAS）和BP神經網絡結合應用于膏體強度的預測中，建立了強度預測模型；吳煒[11]建立了充填體強度ANN-PSO的預測模型；張英坤[12]將灰色系統GM與RBF神經網絡相融合，提出基于GM-RBF神經網絡的混凝土碳化深度預測模型。相對于礦井其他常用充填材料，固體廢棄物膏體充填體組成成分復雜，性質不穩定，其強度特性受多因素耦合控制，且與各因素之間存在高度不規律非線性、模糊復雜性的關系，很難采用常規理論分析的方法進行研究；而灰度理論和神經網絡在處理高度不規律非線性和模糊復雜不確定性問題上有著天然優勢[13]。因此，研究分析了固體廢棄物充填體強度影響因素，進行多因素多水平正交試驗；采用GRA確定各影響因素與充填體強度之間的關聯度，從而確定BP神經網絡輸入層的維數；利用BP神經網絡建立固體廢棄物充填體強度預測模型，對固體廢棄物充填體強度預測探索出了1種新的方法。

1 固體廢棄物充填體強度影響因素

固體廢棄物充填體的加工工藝如圖1。

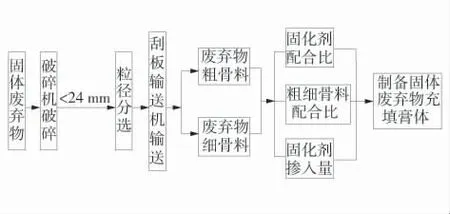
圖1 固體廢棄物加工工藝Fig.1 Solid waste processing technology

常見的礦山膏體充填體，影響其強度的因素主要有料漿的質量濃度、水泥摻量以及骨料級配等。研究結合固體廢棄物充填體自身特點提出以下幾個強度影響因素。

1）固體廢棄物中的混雜纖維。生活垃圾中纖維成分約占1%～5%[14]，包括聚丙烯、聚丙烯腈、尼龍等彈性模量較低和鋼纖維、碳纖維等彈性模量較高的纖維。劉毅[15]通過實驗對比分析了素混凝土與混雜混凝土的抗壓強度，發現摻入混雜纖維可使混凝土抗壓強度提高10%～20%，但纖維摻入量不宜大于3%。廢棄物膏體充填體作為1種似混凝土材料，混雜纖維對其抗壓強度也應有相似作用規律。但用于充填的固體廢棄物，經過破碎、篩選工藝，纖維含量不超過0.6%，因此試驗中混雜纖維含量最大為0.6%。

2）固化劑的配比與摻入量。常用膏體充填體主要選取水泥作為固化劑，雖然水泥能夠極大的提高充填體強度，然而其價格較高。粉煤灰、煤矸石等固體廢棄物可以作為固化劑代替部分水泥，降低充填的成本。試驗中固化劑包括高活性固化劑與低活性固化劑，高活性固化劑由水泥組成，低活性固化劑由煤矸石和粉煤灰組成。賈珍[16]研究了粉煤灰-水泥作為固化劑對固體廢棄物充填體強度的影響，其固化劑配合比為7/3與4/1，摻入量為5%、10%、15%。但試驗中材料取自陳年廢棄物，有機質含量已有所降低，故試驗設定固化劑配合比（低活性：高活性）為5/5～8/2，固化劑摻量分別為骨料的10%～25%。

3）粗細骨料比例。原生固體廢棄物成分復雜、形體尺寸差異較大，不宜直接用于作充填骨料，必須進行破碎、篩分。煤礦充填工藝中，要求骨料的最大粒徑小于輸送管徑的1/5，通常用于煤礦充填的輸送管道直徑為120 mm，因此充填體骨料的最大粒徑必須小于24 mm。研究中定義固體廢棄物充填體骨料粒徑小于5 mm為細骨料，5～24 mm為粗骨料。張新國[17]通過試驗得到，充填體骨料級配中，粗細骨料的比例為3∶8時充填體的綜合性能最好。由于材料的差異性，試驗中粗細骨料比例分別為2/8～5/5。

4）殘余有機質（除纖維外）。早在20世紀80年代，有學者已研究利用有機物廢料制作低造價混凝土[18]。對于煤礦井下充填，在充填體強度達到要求的條件下，一定量的殘余有機質并不影響充填效果。目前我國城市固體廢棄物中80%～90%為建筑垃圾[19]，而用于充填的固體廢棄物經過破碎、篩選等工藝，大部分不適宜于井下充填的有機物已經剔除，但仍殘余部分有機質顆粒，如紙張、塑料等，其含量不大于4%。所以，試驗中殘余有機質含量為1%～4%。

2 固體廢棄物充填體正交試驗及試樣抗壓強度

2.1 正交試驗材料和設備與方法

1）試驗材料。①礦山膏體充填體的原料：煤矸石取自海州露天礦，生活垃圾和建筑垃圾取自阜新市某垃圾場；②固化劑：金隅牌PO42.5普通硅酸鹽水泥，阜新市發電廠Ⅱ級粉煤灰，阜新海州露天礦煤矸石；③減水劑：西卡萘系高效減水劑，減水率約為20%，摻量以固化劑用量1%計算；④早強劑：為了使固體廢棄物充填體早期就具有較高的承載性能，加入價格較低的CaCl2早強劑，摻入量為固化劑的1%；⑤普通自來水；⑥其他廢棄物。

將經過篩分、破碎后的固體廢棄物顆粒作為骨料，制備成廢棄物充填體。試驗中，制備試件為150 mm×150 mm×150 mm的立方體，在溫度為（20±2）℃、相對濕度為95%以上的潮濕環境中養護28 d。

2）試驗設備與方法。試驗采用WAW-600C型微機控制電液伺服萬能試驗機，以0.3 MPa/s的速度加載，直至試件破壞。為提高試驗準確性，同種配比的試件數為3個，強度取其平均值。

2.2 正交試驗設計及試驗結果

為了獲取完備的試驗數據，設計5因素4水平正交試驗，具體因素為固化劑摻入量、不同活性固化劑配合比、纖維摻入量、殘余有機質含量以及粗細骨料比例，試驗選用5因素4水平L16正交表。正交試驗因素水平見表1。

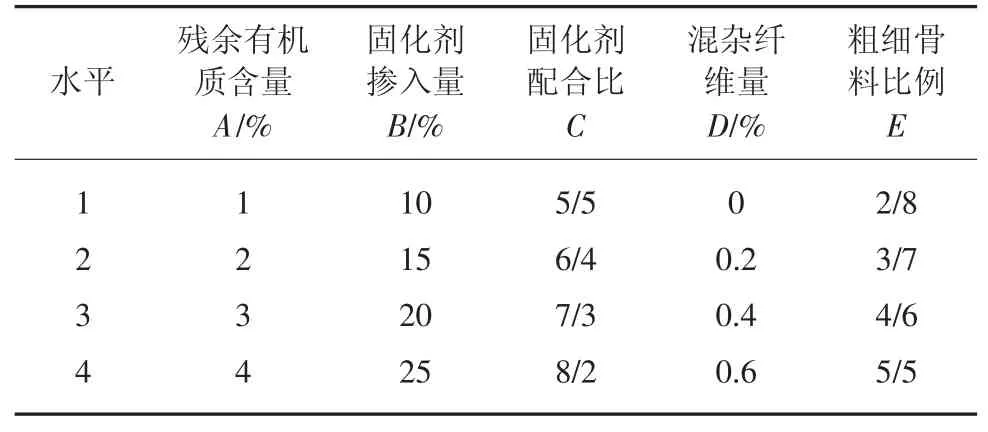
表1 正交試驗因素水平Table 1 Factor and level of orthogonal test

制備固體廢棄物充填體，以骨料為10 kg計算，其作為1種似混凝土材料，參照JGJ 55—2011《普通混凝土配合比設計規程》，充填體試件水膠比采用0.47。正交試驗以M1組為基準組，各組試驗配合比及固體廢棄物充填體試件抗壓強度測定結果見表2。

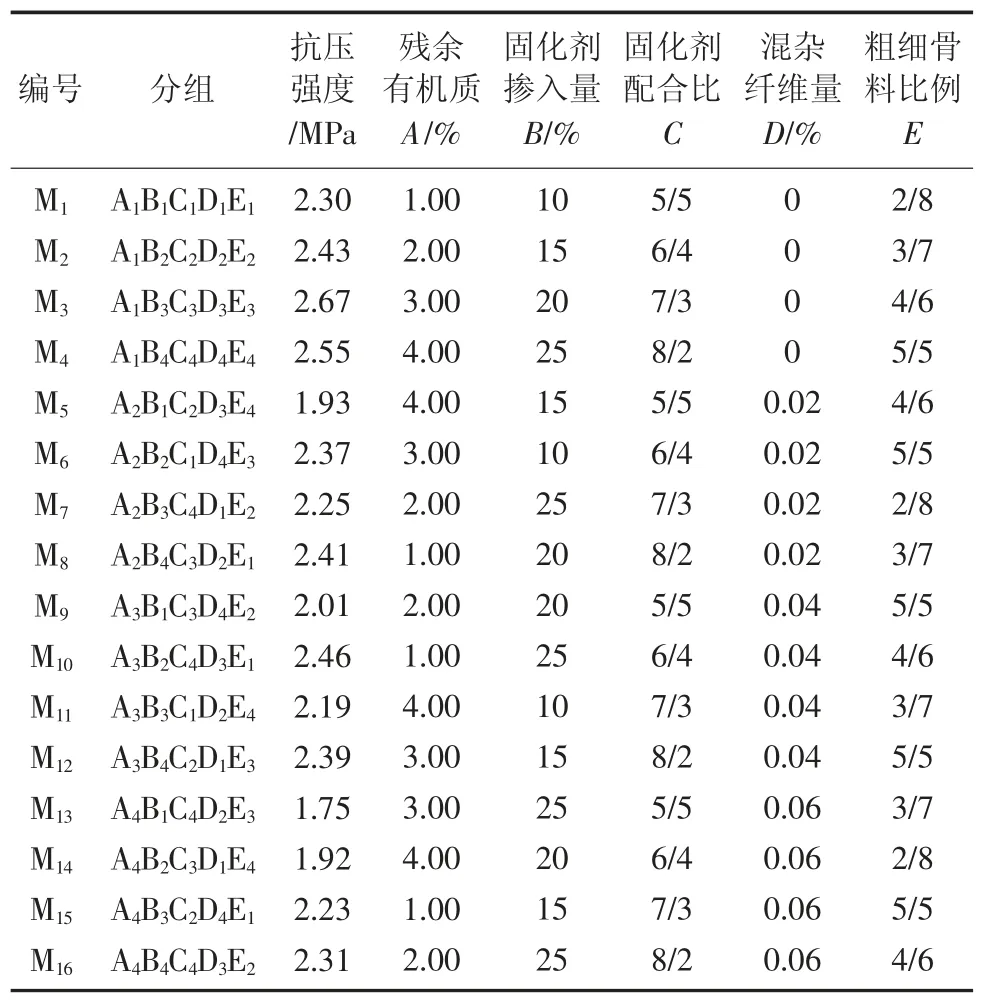
表2 L 16（45）正交試驗配合比設計及試驗結果Table 2 Mix proportion design of L16（45）orthogonal test and test results

3 GRA原理及數據處理

3.1 原始數據處理

由于影響固體廢棄物充填體強度的各因素數據物理意義不同，而且量綱也不同，因此首先要對原始數據作無量綱化處理，常用的方法有初值化處理和均值化處理，研究中采用均值化處理。

設置原始數列，原始數據見表3。

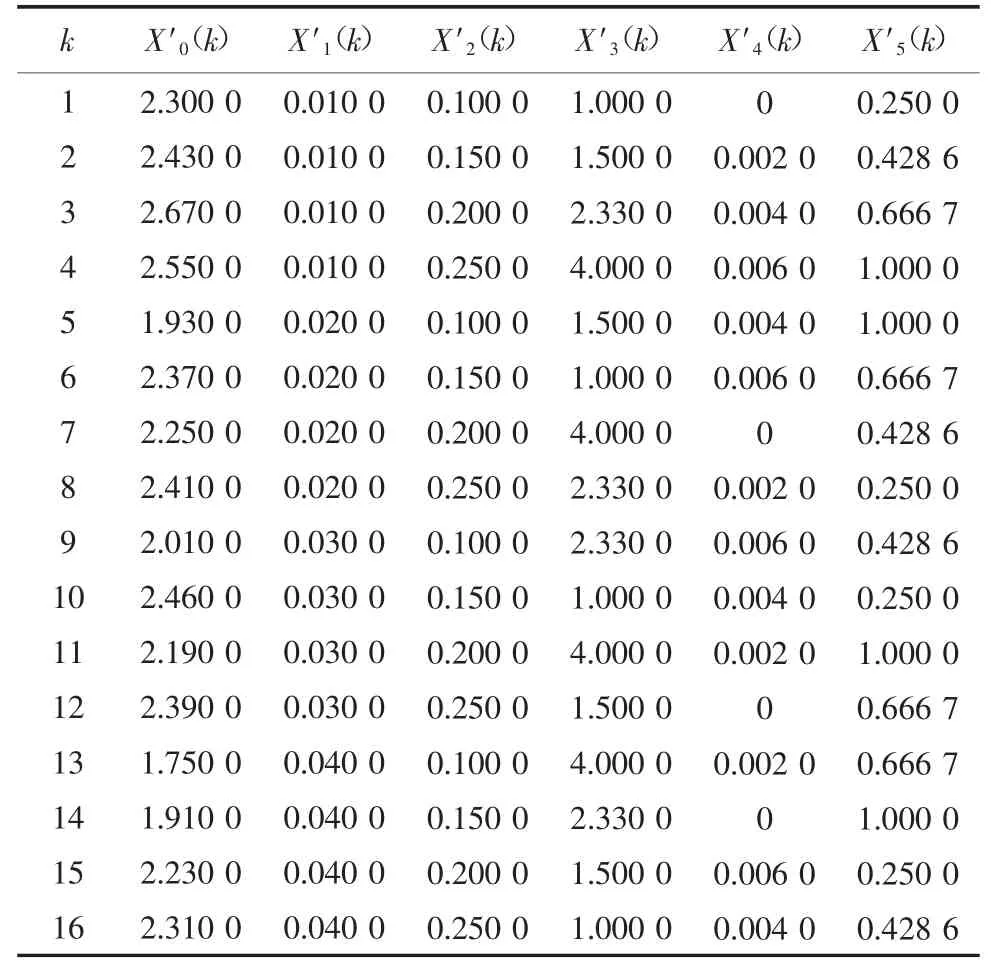
表3 原始數據Table 3 Raw data

將原始數據按式（1）和式（2）進行均值化處理[20]：

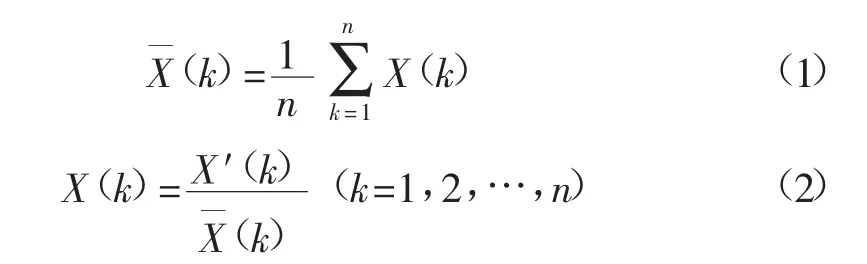
原始數據均值化處理結果見表4。

表4 均值化處理結果Table 4 Results of average processing

接近度計算按式（3）計算[20]：

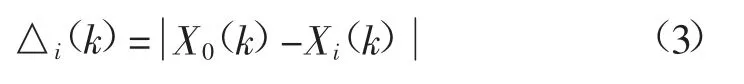
式中：△i（k）為第k個時刻X0與Xi的絕對差。

接近度計算結果見表5。

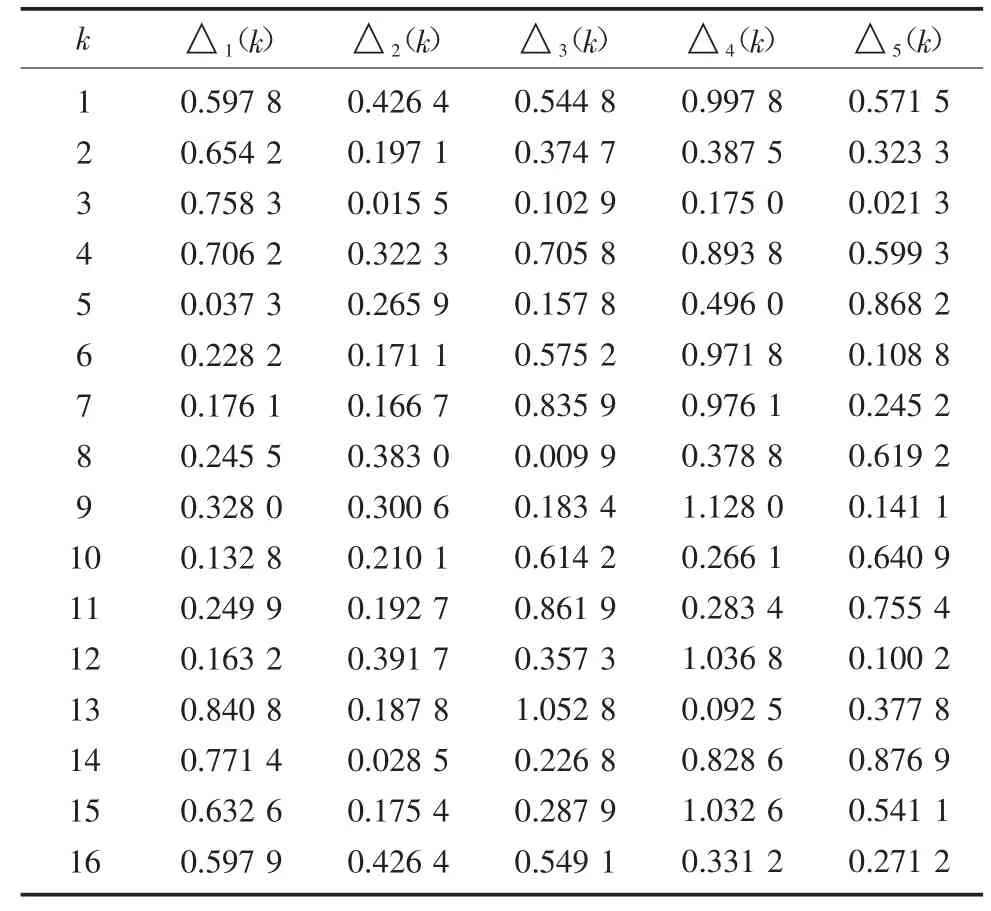
表5 接近度計算結果Table 5 Results of proximity calculation

3.2 關聯系數計算

設X0=｛X0（k）｜k＝1，2，…，n）｝為母數列，Xi=｛Xi（k）｜k＝1，2，…，n）｝，（i＝1，2，…，n）為子數列，X0（k）對Xi（k）的關聯系數ξi（k）按式（4）計算[21]。

經計算，△max＞3△v，即ε△≤ρ≤1.5ε△。由于△max較大，對削弱△max的作用較大，故分辨系數ρ取較小值0.310 7。根據表5接近度計算結果，計算關聯系數，關聯系數計算結果見表6。

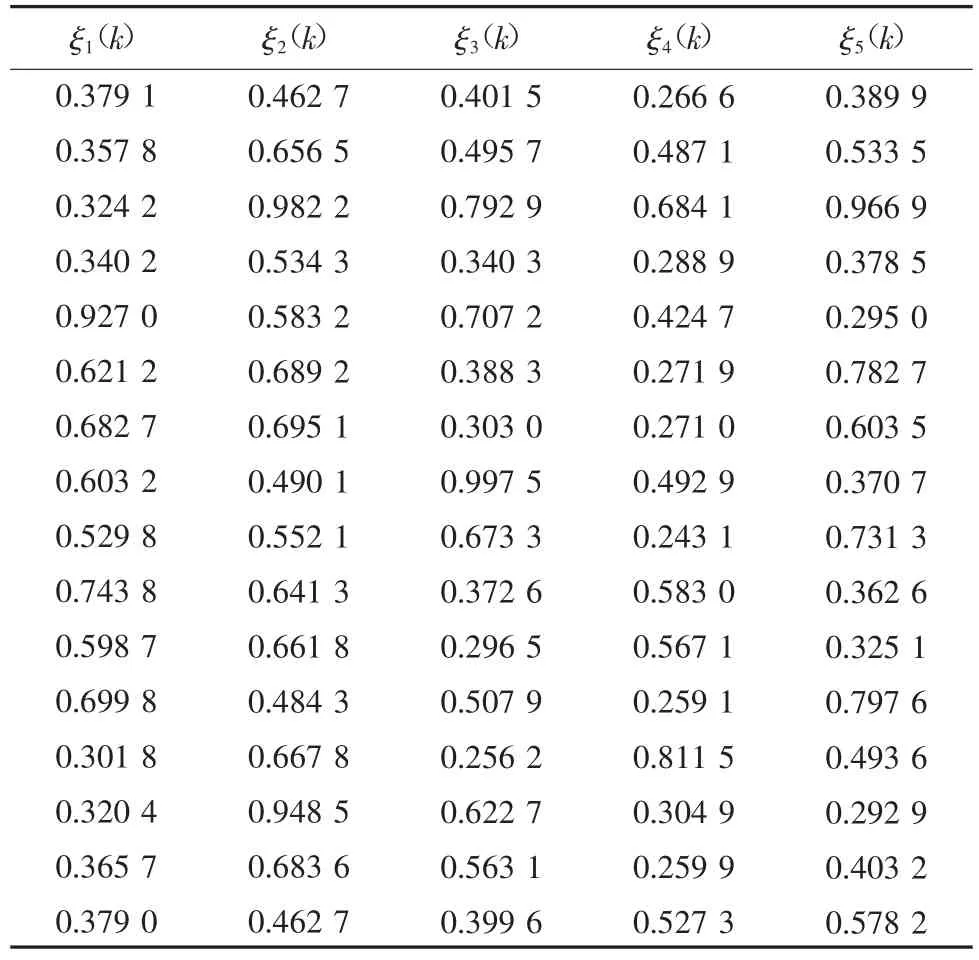
表6 關聯系數計算結果Table 6 Results of correlation coefficients

3.3 關聯度計算

關聯度計算的平均值法數學模型為[21]：

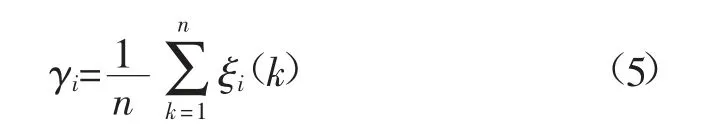
式中：γi為第i個強度影響因素Xi對應于固體廢棄物充填體強度X0的關聯度。

對γi計算結果進行排序，即得充填體強度的灰關聯序。若設灰關聯序為γ1＞γ2＞γ3、…、γm，則表明X1對X0的影響程度最大。

根據式（5），計算得：γ1=0.510 9，γ2=0.637 2，γ3=0.507 4，γ4=0.421 4，γ5=0.515 1。由此可知，各影響因素與充填體強度的灰色關聯序為：γ4（混雜纖維摻入量）＜γ3（固化劑配合比）＜γ1（有機質含量）＜γ5（粗細骨料比例）＜γ2（固化劑摻入量），且一般認為關聯度大于0.3，則相關關系顯著。

由計算可知γi（1，2，…，5）均大于0.3，且相差不大，則其與充填體強度均有較大的相關性。因此，在使用BP神經網絡對固體廢棄物充填體的強度進行預測時，網絡輸入層維數為5。

4 改進的BP神經網絡預測固體廢棄物充填體強度

固體廢棄物充填體神經網絡模型如圖2。

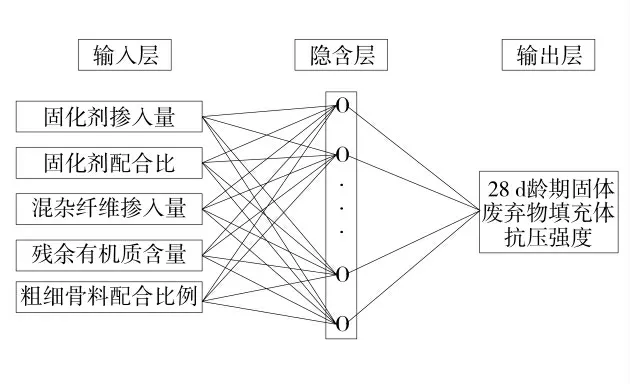
圖2 固體廢棄物充填體神經網絡模型Fig.2 Neural network model of solid waste filling

4.1 BP神經網絡在充填體強度預測中的適用性

BP神經網絡自適應性、非線性函數擬合能力以及結構參數的可調性和固體廢棄物充填體強度影響因素與強度之間的模糊復雜性、不規律的非線性以及參數時變性相契合。使用BP神經網絡預測固體廢棄物充填體強度，無需知道固體廢棄物充填體強度與各影響因素之間的函數關系。只需將完備的強度測試數據作為訓練樣本輸入網絡，接下來網絡開始自動進行訓練和學習，并不斷調整網絡的權值、閾值，最終獲得強度影響因素與充填體強度之間準確的映射關系。根據BP神經網絡特征，任意1個簡單的3層BP神經網絡，在網絡結構參數設置合理的基礎上，能夠以任意精度逼近任何1個非線性連續函數，故BP神經網絡具有擬合高度非線性函數能力，而通過對強度測試數據觀察發現，各因素與充填體強度之間存在不規律的非線性關系，兩者實現良好的吻合。隨著以后對固體廢棄物充填體這種新型充填材料研究深入，可能會提出更多的強度影響因素，影響因素的數目決定著網絡輸入層神經元個數，而BP網絡輸入層神經元數目可隨著影響因素增減而調整[22]。

4.2 傳遞函數的改進

針對傳統傳遞函數Simgoid在f（x）值趨于0或者1時，其導數值將趨近于0，對權值的調整陷入停滯，網絡陷入局部最優陷阱，為此在其基礎上對傳遞函數進行修正改進，修正后的函數如下：

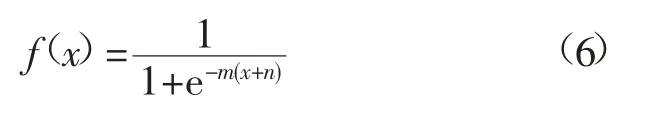
該函數定義域為（-∞，+∞），值域為（0，1），在整個定義域屬于單調遞增連續有界函數，由Hornik理論可知，修正后的函數可以作為網絡傳遞函數。m和n為函數的可變參量，其中n控制函數在水平方向的偏移量，m控制函數的伸縮變化量。2個可變參量的引入使得傳遞函數圖像可以進行水平移動以及伸縮變換，從而傳遞函數具有更強的非線性映射能力。改進傳遞函數（m=2，n=1）與傳統傳遞函數Simgoid（m=1，n=0）性能對比如圖3。

從圖3（a）可知，sigmoid傳遞函數經過改進后其函數值的增長率變得更大，這說明前者的收斂速度大于后者；在x微小區間內，前者相對于后者反應更加靈敏。從圖3（b）可以看出，在橫坐標取相同值時，前者的導數值更大，這表明前者對網絡權值和閾值的修正幅度更大，這就減少了網絡達到目標誤差時的消耗時間，而且傳遞函數經過改進后能夠避免網絡陷入誤差曲面平坦區域，故改進后傳遞函數能夠使網絡部分性能得到優化。

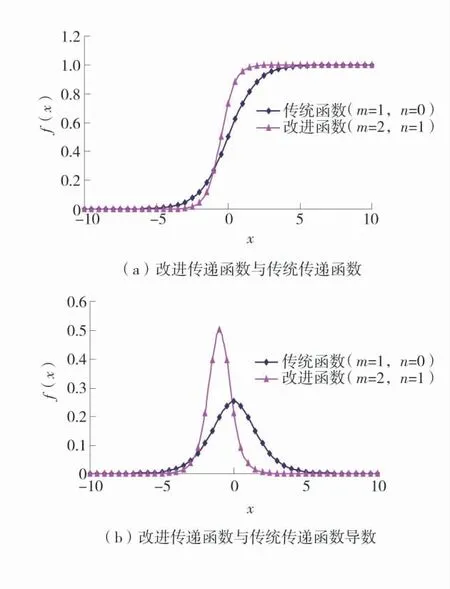
圖3 改進與傳統傳輸函數性能對比Fig.3 Performance comparison between improved and traditional transmission functions

4.3 基于GRA的BP神經網絡模型構造

由Kolmogorov定理可知，1個簡單的3層BP神經網絡能夠準確模擬充填體強度影響因素與充填體之間復雜的非線性映射關系，因此網絡結構層數設計為3層，即輸入層為1，隱含層為1，輸出層為1。

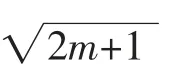
圖4 網絡誤差訓練曲線Fig.4 The network training error curves

隱含層不同單元數網絡學習誤差見表7。隱層節點數為7時，網絡的最終學習誤差最小，在此基礎上繼續增加節點數，其學習誤差增大，網絡對測試樣本的泛化能力會降低。結合學習誤差和收斂速度這兩個網絡性能考慮，文中隱層節點數設置為7。因此網絡的拓撲結構為5-7-1。

表7 隱含層不同單元數網絡學習誤差Table 7 Online learning error for different hidden layer unit number

以正交試驗強度測定數據為基礎樣本，前13組數據用于網絡的訓練，后3組數據用于網絡的測試。運用Matlab軟件創建BP網絡，以5個固體廢棄物充填體強度影響因素作為網絡輸入，以28 d齡期固體廢棄物充填體強度作為網絡輸出，隱層傳遞函數為改進后的函數f（x）=1/（1+e-2(x+1)），輸出層傳遞函數為線性函數purelin，訓練函數為L-M優化算法函數trainlm。經過多次試驗比較，最終設置最大迭代次數為200次，目標誤差為0.000 1，學習率為0.1，其余參數為網絡默認值，當迭代步數為29步時，達到目標精度。

為了確保建立的網絡模型具有優良的性能，對已經建立的網絡進行仿真模擬，訓練樣本檢驗網絡的數據擬合能力，測試樣本檢驗網絡的泛化能力。抗壓強度仿真效果如圖5，抗壓強度仿真相對誤差如圖6。

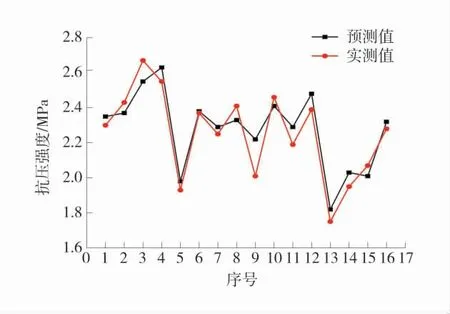
圖5 抗壓強度仿真效果Fig.5 Simulation effect of compressive strength

圖6 抗壓強度仿真相對誤差Fig.6 Simulation relative error of compressive strength

由圖5、圖6可看出，網絡預測模型仿真的充填體抗壓強度相對誤差為0.42%～10.88%，誤差大于5%的僅占6.25%，如圖6中第9點。對于樣本個別點處出現的誤差，原因可能是該點附近訓練樣本的缺乏，其未得到充分訓練，使得樣本空間在此處沒有真實反映網絡輸入與輸出之間的映射關系。即使如此，建立的模型仍具有較高的精度，是其他數學處理方法難以達到的。

以上BP網絡模型不僅可以用于固體廢棄物充填體強度的預測，而且也可以用于強度要求相似的固體廢棄物充填體配合比設計。

5 結語

1）分析總結了影響固體廢棄物充填體強度的5個因素—混雜纖維、固化劑摻入量、不同活性固化劑配合比、粗細骨料比例以及殘余有機質含量。

2）運用GRA確定了固體廢棄物充填體強度影響因素與定量關聯度，并進行了灰關聯度排序，確定了BP神經網絡輸入層的維數為5。

3）建立了5-7-1BP神經網絡充填體強度預測模型，檢驗了網絡的數據擬合能力以及泛化能力，檢驗結果表明，網絡達到了93.75%的預測精度，能夠實現對充填體強度的準確預測。