發(fā)掘隱性信息 拓寬解題思路
周銀生
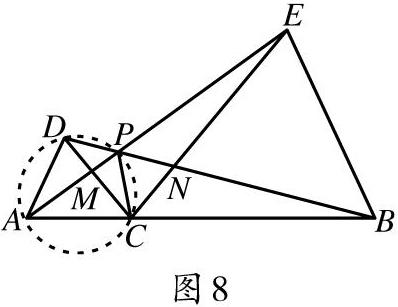

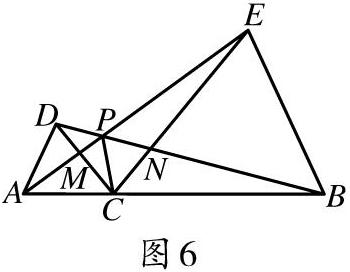
[摘 要]有關(guān)“隱圓”的問題是近年考試中常考的內(nèi)容,需要引起教師的重視.所謂“隱圓”通常體現(xiàn)的是“四點(diǎn)共圓”的問題.在解決若干點(diǎn)相對(duì)位置的問題中找出隱含條件,發(fā)現(xiàn)“隱圓”,有助于打開思路、找到破題點(diǎn).
[關(guān)鍵詞]四點(diǎn)共圓;平面幾何;隱性;解題
[中圖分類號(hào)]? ? G633.6? ? ? ? [文獻(xiàn)標(biāo)識(shí)碼]? ? A? ? ? ? [文章編號(hào)]? ? 1674-6058(2021)29-0018-03
初中階段的平面幾何,主要是要求學(xué)生掌握常見幾何圖形的邊邊之間、角角之間和邊角之間的關(guān)系.圓是平面幾何中的一個(gè)主要考點(diǎn),其內(nèi)部、邊界上和外部的角、邊之間具有很多關(guān)系.可以利用圓的相關(guān)性質(zhì)進(jìn)行快速判定,特別是“隱圓”特性形成的新解題思路值得我們探討.
一、形成“隱圓”(“四點(diǎn)共圓”)的基本條件
由圓的基礎(chǔ)定義可以得到,圓上的任意一點(diǎn)到圓心的距離是相等的.反過來說可以理解為確定一個(gè)固定點(diǎn),所有到這個(gè)定點(diǎn)的距離相等的點(diǎn)都在同一個(gè)圓的邊界上,這是“四點(diǎn)共圓”理論的定義起點(diǎn),也是一切解題思路的出發(fā)點(diǎn),這個(gè)條件可以衍生出以下幾個(gè)具有代表性的問題,需要我們進(jìn)一步研究和思考.
該方法的運(yùn)用與學(xué)生通常利用的角的相互轉(zhuǎn)化來證明角相等的方法較為適應(yīng),順應(yīng)了學(xué)生的解題思路,降低了該題的分析難度.而關(guān)鍵的要點(diǎn)在于找到共同的圓所在,這就要對(duì)“隱圓”的條件和圓有關(guān)的特性知識(shí)點(diǎn)進(jìn)行全面的掌握和理解.
初中生在做題過程中要做到思維開闊,對(duì)定理和知識(shí)要爛熟于心,要對(duì)“隱圓”兩個(gè)條件的推導(dǎo)過程和結(jié)論熟練掌握,在遇到證明公共邊的三角形或四邊形角相等的問題時(shí),有意識(shí)地考慮是否可用到“隱圓”,這樣對(duì)解題思路的破解有一定的幫助.
[? ?參? ?考? ?文? ?獻(xiàn)? ?]
[1]? 仲惟超.發(fā)掘隱性信息,開拓解題思維:以平面幾何問題中的“隱圓”為例[J].數(shù)學(xué)學(xué)習(xí)與研究,2019(22):149+151.
[2]? 戴娟.微專題在中考數(shù)學(xué)二輪復(fù)習(xí)中的實(shí)踐與思考:以“探尋與隱圓有關(guān)的最值與路徑問題”為例[J].中學(xué)數(shù)學(xué)月刊,2018(11):23-25.
[3]? 王弟成.高中數(shù)學(xué)“隱圓”問題的特點(diǎn)與解法:以一道高二學(xué)業(yè)質(zhì)量調(diào)研試題為例[J].教育研究與評(píng)論(中學(xué)教育教學(xué)),2019(6):48-52.
[4]? 竺寶林.基于“策略與方法聯(lián)想”的高三習(xí)題講評(píng)模式的嘗試:以一道南京市期初調(diào)研試題為例[J].中小學(xué)數(shù)學(xué)(高中版),2018(10):48-50.
(責(zé)任編輯 黃桂堅(jiān))

