高比例新能源電網多源最優協同調頻策略
何廷一,李勝男,陳亦平,吳水軍,沐潤志,和鵬,孟賢,何鑫,楊博,曹璞璘
(1.云南電網有限責任公司電力科學研究院,昆明市 650200;2.中國南方電網電力調度控制中心,廣州市 510663;3.云南電力試驗研究院(集團)有限公司,昆明市 650200;4.昆明理工大學電力工程學院,昆明市 650500)
0 引 言
近年來,為減少對化石燃料的依賴,世界各國致力于發展以風光為代表的新能源。但風電機組、光伏機組的輸出在很大程度上受天氣的影響,其發電出力存在較大的隨機波動,使得發電側“棄風”、“棄光”等現象常有發生[1-3]。因此,為避免該現象的發生,有必要對其展開研究,使之成為優質的調頻資源,緩解傳統水火電廠的調頻壓力,加快系統調頻的動態響應性能。
電網調頻技術的應用旨在當電網受到負荷變化擾動時,將電網的頻率控制在穩定范圍內。傳統的調頻機組主要由水、火電機組來構成,其調節慣性較大,難以快速響應功率輸入命令[4]。近年來,隨著新能源機組的大規模并網,其輸出依靠電力電子設備調節,可以快速響應動態的功率輸入調節命令,因此,風電機組、光伏機組可采用定功率點控制方式,將其控制在低于最大功率點的運行工況,留有一定的備用容量參與到二次調頻[5]。
目前,二次調頻工程領域常根據可調容量來按比例地分配各機組輸出功率,該方法稱為按比例分配(proportion method,PROP),但該策略無法滿足系統最優控制需求[6]。另外,目前風光新能源參與調頻的大部分研究主要關注控制器的設計、風電場及光伏電站自身的控制策略,較少研究風光新能源與其他調頻資源之間的協同控制。因此,有必要開發風光電站與傳統水火電站之間的最優協同調頻方法。文獻[7]建立了多源互補控制模型,實現了多源協同互補控制。文獻[8]構建了包含風電、光伏及抽水蓄能電站收益的多目標函數,實現了風光新能源與其他調頻資源的協同控制。文獻[9]建立了二次調頻指令最優分配模型,并采用基于改進策略的優化算法求解該模型。但上述文獻建模相對簡單,未考慮各機組間的動態響應特性。另外,該問題為復雜的非線性優化問題,傳統的數學方法具有搜索能力差,難以獲得全局最優的缺陷。與之相比,多目標遺傳算法(non dominated sorting genetic algorithm-Ⅱ,NSGA-Ⅱ)[10]、基于強度Pareto進化算法2(strength pareto evolutionally algorithm 2,SPEA2)[11]等多目標智能優化算法具有收斂速度快等優點,但全局搜索能力還有待提高。
為此,本文嘗試搜索能力更強、收斂速度更快的多目標蝠鲼覓食優化算法(multi-objective manta ray foraging optimization,MMRFO)進行求解,其可以獲得分布更加廣泛、更加均勻的Pareto前沿,并基于熵權法,設計灰靶決策法客觀地選擇折中解,可以得到最優經濟條件下具有最小功率響應總偏差的功率分配方案。為驗證該方法的有效性,本文采用基于擴展的兩區域負荷頻率控制(load frequency control,LFC)模型進行驗證。
1 多源協同互補控制模型
1.1 控制框架
基于擴展的兩區域LFC模型的調頻框架如圖1所示。其中,ΔPT為聯絡線功率偏差;Δf為實時頻率偏差;ΔPout為實際功率調節輸出;ΔPD為負荷擾動[12]。另外,電網調頻控制技術主要由控制器和功率優化分配2個環節組成,控制器通常采用PID控制方式,將實時頻率偏差Δf和聯絡線功率偏差ΔPT作為輸入,輸出整個區域電網的實時總調節功率ΔPC,隨后由功率分配算法分配ΔPC至各個調頻機組。
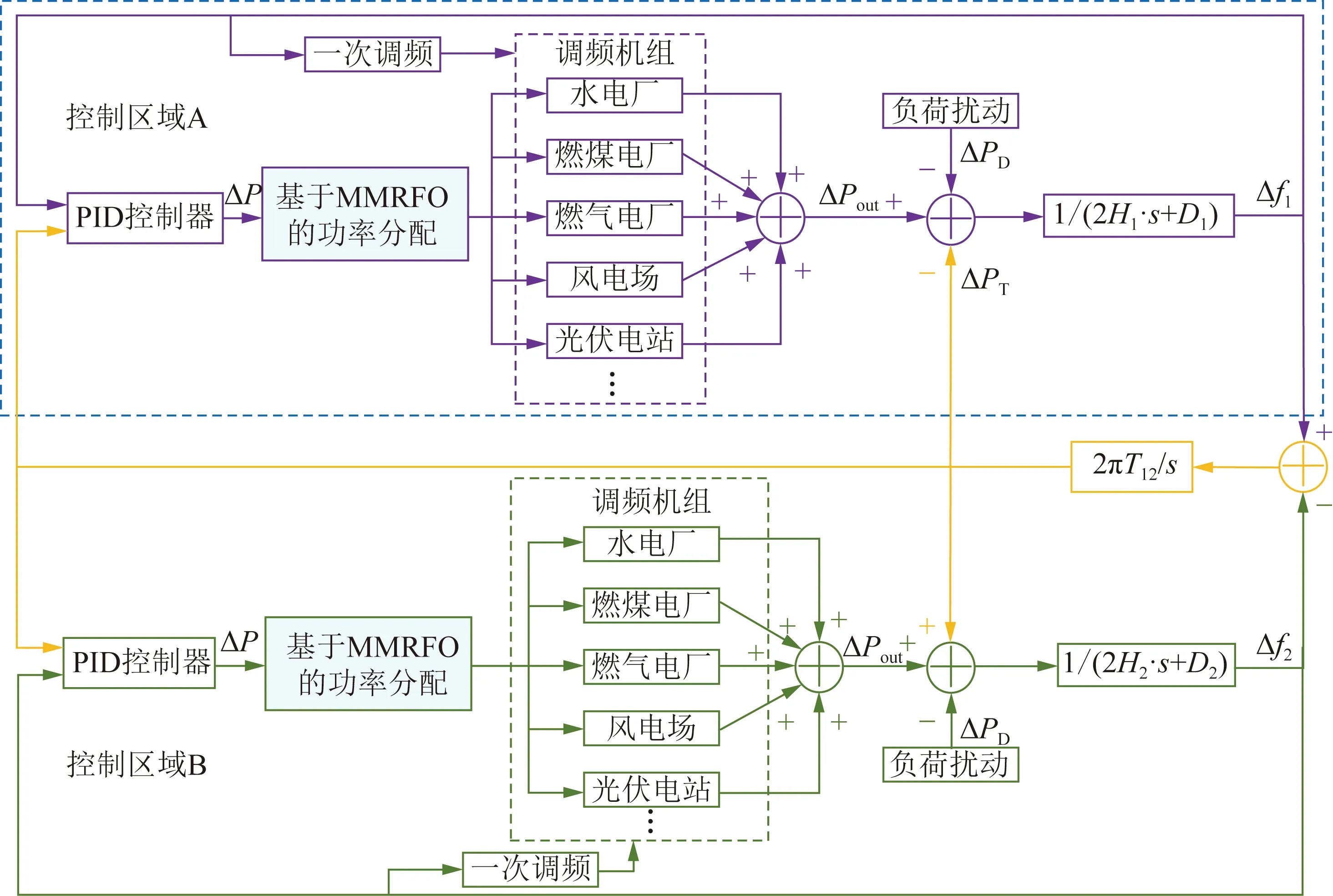
圖1 基于擴展兩區域LFC模型的調頻框架Fig.1 Framework of frequency regulation on extended two-area LFC model
1.2 約束條件
功率分配過程中,為保證電力系統的穩定運行,須重點考慮功率平衡約束、爬坡約束(generation ramp constraint,GRC)、機組容量約束、能量傳遞約束[12]。
1)功率平衡約束。
在第k個控制周期內,控制器輸出的實時總調節功率應等于所有調頻機組接收到的功率調節輸入指令之和。
(1)
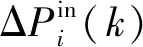
2)機組容量約束。
(2)
(3)

3)GRC和能量傳遞約束。
表1和圖2分別給出了考慮GRC和機組容量約束的不同類型調頻機組的動態響應傳遞函數和動態響應模型。其中,Td為機組二次調頻時延;G(s)為機組功率響應傳遞函數。若不考慮GRC和功率輸出限制,實際調節功率輸出可通過頻域傳遞函數的拉普拉斯逆變換得到[13]。
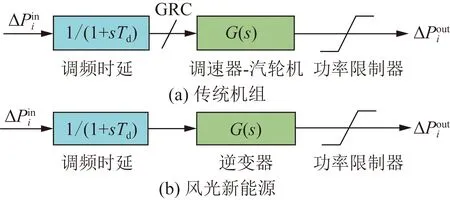
圖2 動態響應模型Fig.2 Dynamic response models

表1 不同類型調頻機組動態響應傳遞函數Table 1 Dynamic response transfer functions of different frequency-regulation units
(4)
(5)
(6)
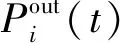
若考慮GRC和功率輸出限制,調頻機組的輸出可改寫為:
(7)
(8)
(9)
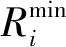
1.3 目標函數
為提升整個區域電網的動態響應性能,設定調節功率指令值和功率響應值的偏差,以及總調頻里程支出最小化作為目標函數,可表示為:
(10)
式中:Ri為第i臺調頻機組的調頻里程支出。
(11)
(12)
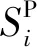
2 多目標蝠鲼覓食優化算法及應用設計
2.1 蝠鲼覓食優化算法
MMRFO受蝠鲼的覓食策略所啟發,其中包括鏈式覓食、螺旋覓食和翻滾覓食。
1)鏈式覓食。
蝠鲼排成有序的頭尾排列,形成一條鏈來捕捉浮游生物。在MMRFO中,蝠鲼鏈的目標獵物為浮游生物,因此,假設目前得到的最佳解為濃度較高的浮游生物群。個體根據當前最優解和前一個個體更新當前位置,如下表示[14]:
(13)
(14)
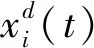
2)螺旋覓食。
當蝠鲼發現深水中有一群浮游生物時,其會采用螺旋的方式進行捕食。在MMRFO中,個體的移動根據前一個個體以及當前最優個體進行更新,該搜索方式可由下式來表示[14]:
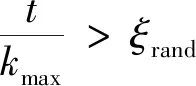
(15)
(16)
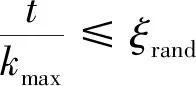
(17)
(18)
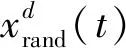
3)翻滾覓食。
在MMRFO中,為提高全局搜索能力,蝠鲼個體會以當前最優解作為支點,進行翻滾操作到與其當前位置成鏡像關系的另一側,如下表示[14]:
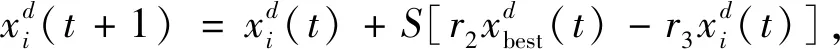
(19)
式中:r2、r3為在[0,1]上均勻分布的隨機數;S為常數,取值為2。
2.2 Pareto解集存儲與篩選
MMRFO會不停更新有限規模的存儲池里Pareto解集以完成迭代過程,該過程中,獲得的新的非支配解會與存儲池里非支配解進行比較,從而判斷新的非支配解是否對存儲池進行更新,其中分為3種情況[15]:
1)若新的非支配解支配存儲池里一個或多個解,則存儲池的非支配解將被新的非支配解進行替換;
2)若存儲池里至少一個非支配解支配新的非支配解,則不進行更新操作;
3)若存儲池里的非支配解與新的非支配解不構成支配與被支配的關系,則將新的非支配解儲存在存儲池中。
為提升算法的搜索效率,須對存儲池的規模進行限制,當非支配解的分布過于密集時,算法將通過下式剔除部分非支配解:
(20)
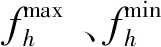
2.3 基于熵權法的灰靶決策法設計
2.3.1效應樣本矩陣的設計
基于MMRFO的Pareto解集X為一個n行m列的矩陣,可將X中各解的絕對值作為決策指標之一,亦可作為Pareto前沿的單位解輸出,如下表示:
X′(i,j)=|X(i,j)|,i=1,2,…,n,j=1,2,…,m
(21)
為了降低總功率偏差和調頻里程支出,2個目標函數值可分別設置為F1和F2。另外,本文引入了一個表示X′中每個解到坐標原點的歐幾里德距離的矩陣D,其元素Di如下所示:
(22)
至此,評估指標一共由m+3個構成,即m個Pareto前沿單位解的輸出,2個目標函數值以及歐氏距離平方矩陣D。進一步,可將其用矩陣表示為:
X″=[X′F1F2D]
(23)
2.3.2靶心矢量設計
基于獎勵最好、懲罰最差原則的算子Zj的計算公式為:
(24)
值得注意的是,所有指標均大于0,且指標越小,代表解的質量更佳,決策矩陣V的元素vij可表示為:
(25)
式中:zij為“獎優罰劣”變換算子;xij為第i個解決方案的第j個目標。
2.3.3靶心設計
本文基于熵權法,設計了灰靶決策法來更客觀地選擇折中解并得到各個目標函數之間的權重,其中,權重yij和熵值Ej的計算公式為:
(26)
(27)
(28)
(29)
至此,靶心距離最小的解,便可選擇為折中解,作為最優的功率分配方案。MMRFO求解流程如圖3所示。此外,圖4給出了在3個連續的控制周期內,獲得的Pareto前沿與被選擇的折中解。
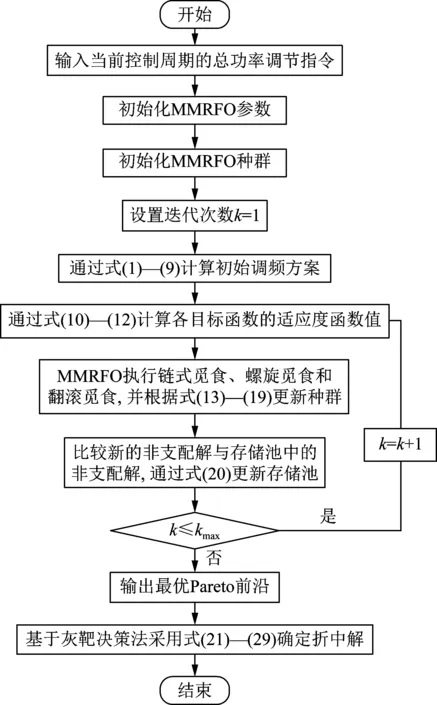
圖3 MMRFO求解流程Fig.3 Flow chart of MMRFO
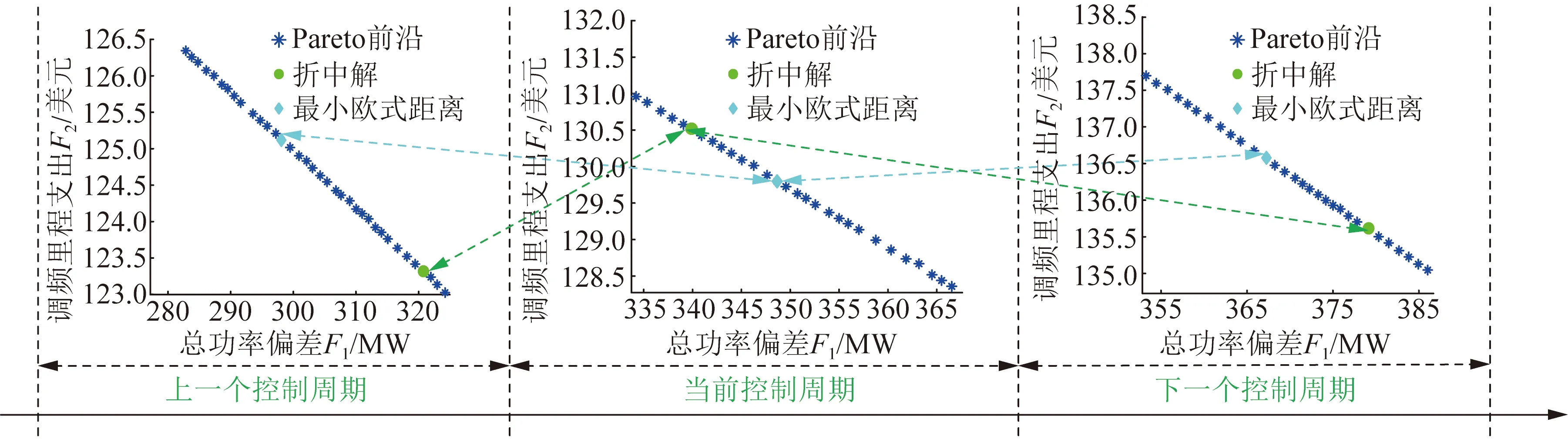
圖4 折中解的選擇Fig.4 The selection of decision options
3 算例分析
為驗證MMRFO以及灰靶決策法的有效性,本文基于擴展的兩區域LFC模型進行測試。并引入基于非支配領域選擇的多目標免疫算法(multi-objective immune algorithm with non-dominated neighbor-based selection,NNIA)[16]、NSGA-Ⅱ[10]以及SPEA2[11]進行比較。為公平比較各算法的搜索性能,所有算法的種群大小和最大迭代次數均分別設置為N=50和kmax=50。其中,調頻控制時間周期為4 s,調頻里程價格為2美元/MW。此外,各機組的傳遞函數參數如表2所示,表3給出了各機組的主要參數。

表2 調頻機組的傳遞函數參數Table 2 Parameters of transfer functions of frequency-regulation units
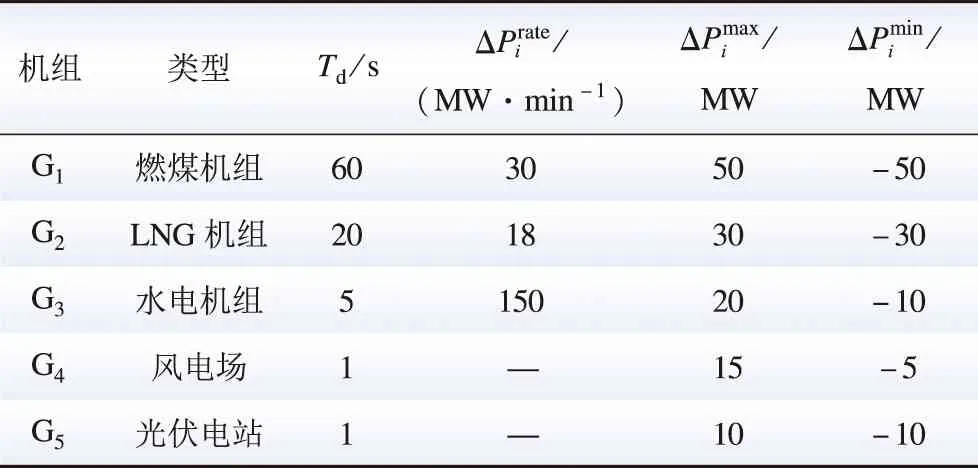
表3 調頻機組的功率調節參數Table 3 Main parameters of power regulation of frequency-regulation units
3.1 算法性能測試
為測試算法遭遇負荷擾動時的調節能力,本算例采用ΔPD=50 MW和ΔPD=-50 MW的負荷擾動進行測試。圖5(a)比較了各算法在ΔPD=50 MW時獲得的Pareto前沿,可以看出,NNIA得到的解明顯偏離理想的Pareto前沿。另外,NNIA、NSGA-Ⅱ和SPEA2在ΔPD=-50 MW時獲得的Pareto前沿表現不佳,如圖5(b)所示。而MMRFO在2種功率擾動下能夠獲取分布最均勻且廣泛的Pareto前沿。
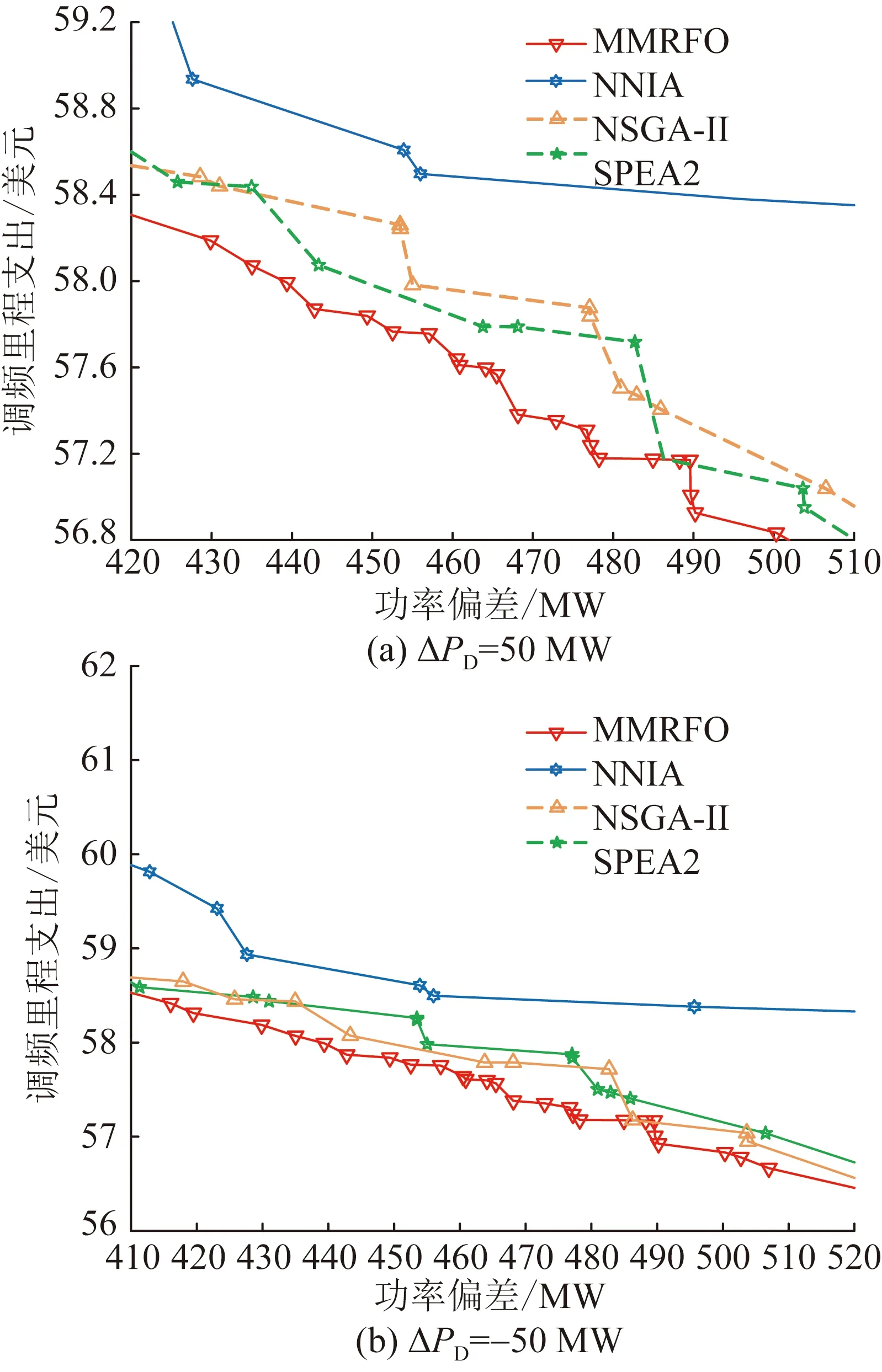
圖5 基于擴展的兩區域LFC模型,4種算法的Pareto前沿比較Fig.5 Comparison of the Pareto front obtained by four algorithms on the extended two-area LFC model
表4給出了各算法運行10次后,包括反轉世代距離(inverted generational distance,IGD)[17]、世代距離(generational distance,DG)[18]、純粹多樣性(pure diversity,PD)[19]、超體積(hyper volume,HV)[20]、分布度指標(diversity metric,DM)[21]、廣泛性[21]、間距[22]以及平均運行時間的8種指標的平均值和標準差,從而比較各算法的搜索性能,可以看出:
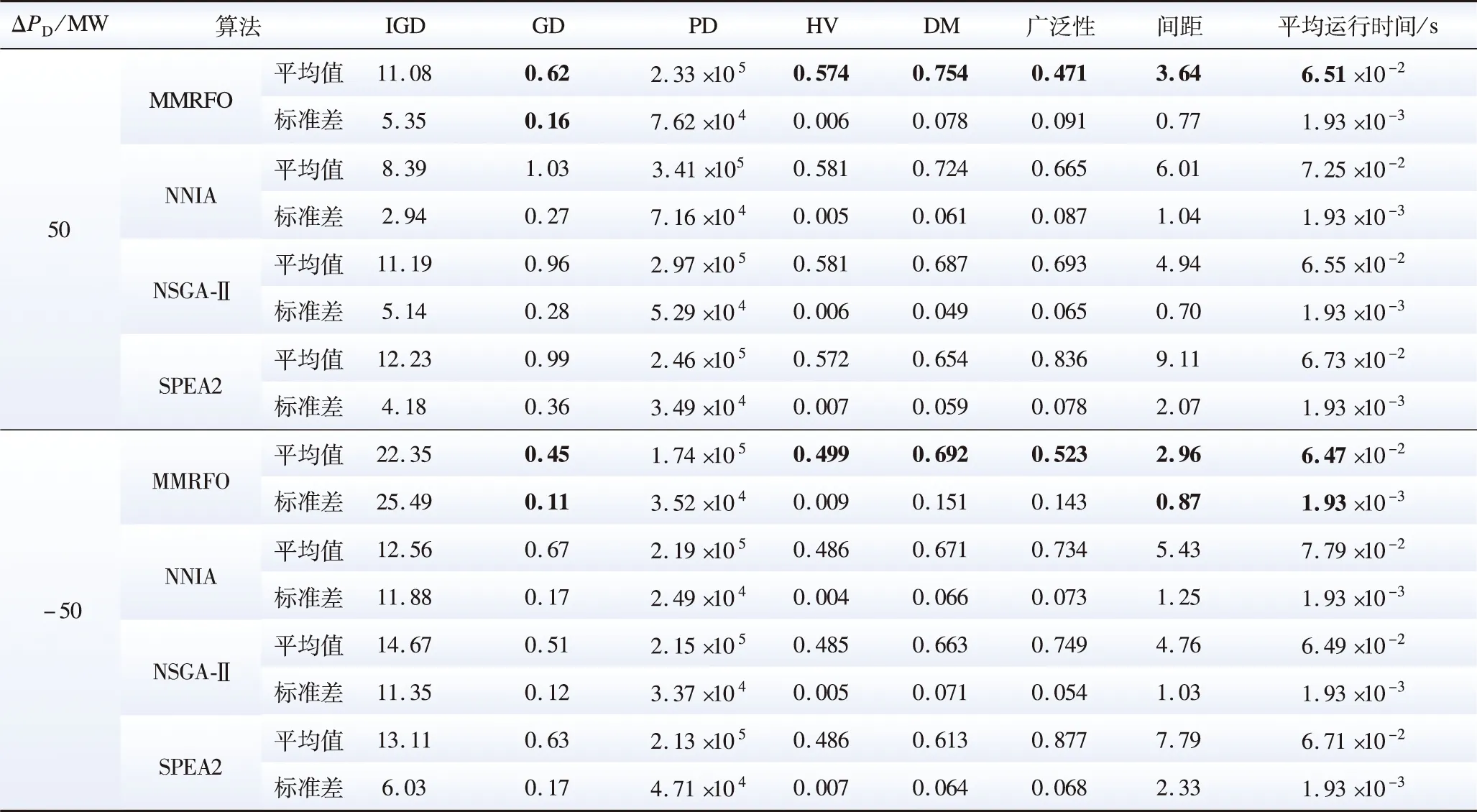
表4 各算法性能比較Table 4 Comparison of performance metrics of algorithms
1)在各算法的IGD、GD平均值中,MMRFO的GD值最小,因此其具有良好的收斂性能;
2)MMRFO的DM和HV平均值明顯大于其他算法,PD平均值略小于其他3種算法,證明了其具有表現良好的Pareto前沿多樣性;
3)MMRFO具有最小的廣泛性、間距平均值,即可證明MMRFO得到的Pareto前沿分布最為均勻且廣泛;
4)MMRFO具有最小的平均運行時間,因此其能夠最快地收斂到Pareto前沿,從而在最短時間內響應功率調節指令。
3.2 負荷階躍擾動測試
為進一步驗證MMRFO以及灰靶決策法的有效性,本算例采用ΔPD=70 MW和ΔPD=-50 MW的負荷擾動進行測試,并與PROP進行比較[6]。因此,基于PROP,第i臺調頻機組在第k個控制周期的輸出計算公式為:
(30)
ΔPD=70 MW、ΔPD=-50 MW時,基于擴展的兩區域LFC模型優化結果分別如圖6、7所示。從圖6(a)可以看出,MMRFO以及灰靶決策法可以很好地協調各機組之間的功率輸出,在ΔPD=70 MW時,獲得的總功率偏差顯著低于PROP。
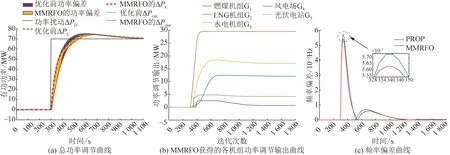
圖6 基于擴展的兩區域LFC模型優化結果(ΔPD=70 MW)Fig.6 Real-time optimization results obtained on the extended two-area LFC model when ΔPD=70 MW
另外,從圖7(a)可以看出,與PROP相比,本文所提方法獲得的功率偏差更小,減少了總功率指令的超調,能夠在更短時間內恢復受到擾動的系統。
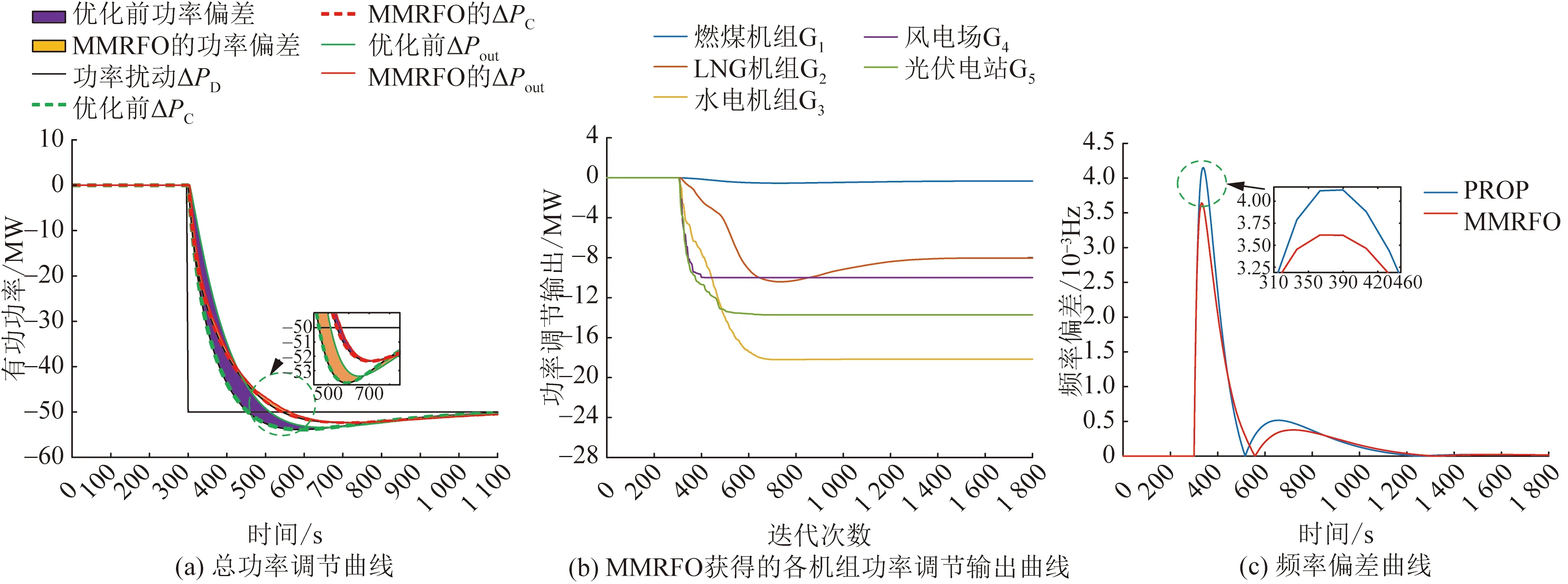
圖7 基于擴展的兩區域LFC模型優化結果(ΔPD=-50 MW)Fig.7 Real-time optimization results obtained on the extended two-area LFC model when ΔPD=-50 MW
圖8給出了不同擾動情況下的調頻里程支出變化。綜合圖6、圖7以及圖8,可以看出,MMRFO能夠在兼顧調頻里程支出的前提下,顯著提升電能質量。
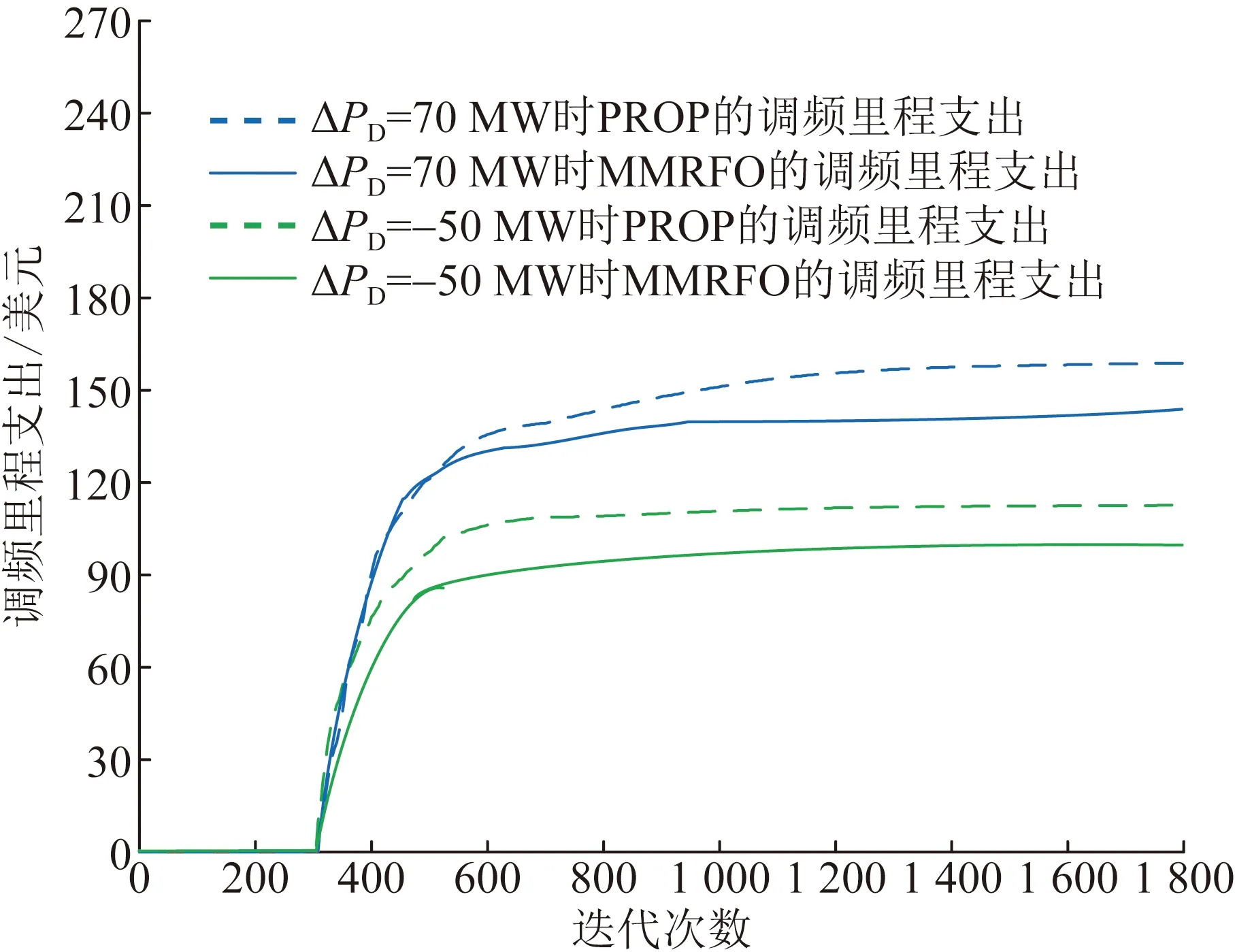
圖8 不同功率擾動下的調頻里程支出Fig.8 Mileage payment of frequency regulation under four perturbations cases
表5比較了2種工況下的在線優化結果,可知MMRFO方法能夠有效減小功率響應總偏差,能夠在滿足CPS(control performance standard)的前提下降低平均頻率偏差|Δf|和區域控制誤差絕對值,并有效提升系統的動態響應性能。其中,CPS考核標準包括2個部分,即CPS1和CPS2。CPS1采用基于統計方法來衡量某控制區區域控制誤差的變化特性及其與系統頻率偏差的關系;CPS2用于評估某控制區域控制聯絡線潮流偏差的能力。本文采用CPS1對所提方法進行評估。

表5 不同擾動下優化結果比較Table 5 Result comparison of online optimization under different perturbations
4 結 論
本文提出了一種基于多目標蝠鲼覓食優化算法的多源最優協同調頻策略,主要貢獻為:1)該策略能夠在最優經濟效益的前提下,有效降低總功率偏差,最優分配各種調頻資源;2)多目標蝠鲼覓食優化算法能夠在最短時間內獲得分布最為均勻且廣泛的理想Pareto前沿,而基于熵權法設計的灰靶決策法可以客觀地選擇折中解,充分發揮各種調頻資源的優勢;3)針對擴展的兩區域負荷頻率控制模型進行測試,其結果顯示區域控制誤差絕對值、平均頻率偏差、總功率偏差得到降低,能夠在獲得最佳經濟性的同時提高動態響應性能,證明了該策略能有效地解決多目標優化問題。
為進一步提高經濟效益以及系統響應速度,未來將研究裝配儲能系統的新能源場站,并嘗試采用深度強化學習解決該問題,實現多源協同互補控制。

