云南電網低頻問題下風機轉子動能控制研究

何廷一，王晨光，李勝男，陳亦平，李崇濤，高琴

(1.云南電網公司電力科學院，昆明市 650217；2.西安交通大學電氣工程學院，西安市 710049； 3.中國南方電網電力調度控制中心，廣州市 510623)

0 引 言

2016年云南電網與南網主網異步互聯后，由于系統慣量小、水電占比高，缺乏快速調頻手段，頻率穩定問題突出。隨著新能源機組投產規模逐步擴大，充分挖掘新能源的快速調頻能力已經成為了業界共識。2019年云南電網開始投入新能源機組一次調頻向下調節功能來改善大容量直流閉鎖后的高頻特性。

直流頻率限制器(frequency limit controller，FLC)[1]定位于大擾動后頻率穩定控制措施。而實際運行時發現，單機甩負荷都會引起直流FLC動作，僅2019年750 MW以內的功率擾動導致直流FLC動作(動作死區為±0.14 Hz)的案例就有十余起，且事故擾動量最小僅有248 MW。如何發揮風電機組一次調頻功率上調節功能，改善電網頻率低周問題也成為研究的關注點。

由于風電、光伏等新能源機組正常運行在最大功率點跟蹤(maximum power point tracking，MPPT)控制下[2]，不具備頻率響應能力，只有改進了自身控制方式[3-6]的風電機組可以通過釋放轉子動能短時上調有功出力。轉子動能控制[3]有虛擬慣性控制、下垂控制和綜合慣性控制。這僅解決了如何讓風電機組具有調頻能力的問題，如何根據系統特性進行控制參數整定，并實現與其他調頻資源的協調，避免轉速恢復帶來的頻率二次跌落問題仍有待深入研究。

目前關于風電與其他調頻資源相互作用對系統頻率影響的研究，多集中在其與常規同步發電機調速器控制協同方面。文獻[7]探討了不同風電滲透率、系統備用容量下，風電并網系統頻率動態控制設計原則。文獻[8]針對不同頻率敏感單元之間的協調問題，指出了風電動態功率支撐會延遲常規同步機組一次調頻動作，從而惡化系統頻率動態，故提出了通過設置協調參數合理調度風電場與常規同步機組的動態功率。目前涉及直流輸電的頻率協同優化主要集中在直流FLC與常規同步機組調速器的協調[9]，關于直流FLC與常規同步機組調速器控制及風電的協調優化設計研究較少。然而，隨著大規模風電并網，直流送端系統中常規同步機組比例減少，系統中的等效慣量和備用容量都減少。因此，研究風電與常規同步機組調速器控制及直流FLC相互作用對系統頻率的影響規律，以提升系統頻率穩定也十分必要。

本文首先分析云南電網的調頻特性以及統調風機潛在調頻能力，提出通過釋放風機轉子動能參與一次調頻改善電網頻率低周問題的必要性和可行性；然后建立包含多類型調頻資源的系統頻率仿真簡化模型；近一步針對云南電網頻率低周問題，研究并提出多調頻資源協調下風機轉子動能控制設計思路及整定方法；最后基于云南電網典型運行場景，驗證風機的調頻效果，分析各風速下風機轉子動能控制參數取值規律，并對比不同風速下風機的調頻能力。為實際工程中將風電調頻在電網頻率低周問題下納入云南電網調頻體系提供一定的參考。

1 云南電網頻率低周問題下風電參與一次調頻的必要性和可行性分析

1.1 新能源高滲透下的調頻問題

隨著以風電為代表的新能源裝機占比的逐步提高，作為送端的云南異步電網呈現出了以下顯著特性：

1)從電源側來看，云南電網水火等常規同步機組的發電空間被擠壓，常規同步機組日常開機減少，電網低慣量運行場景已經在系統小負荷運行方式下出現。云南電網本身是高比例水電系統，受水輪機“水錘效應”影響，水電機組3～5 s內的快速一次調頻能力缺乏，導致云南電網在系統頻率為0.04～0.07 Hz范圍內缺乏快速調頻手段，頻率波動頻繁。

2)從負荷側來看，在系統中等負荷或大負荷運行方式下，云南電網直流外送電量超過本地負荷使用電量，直流系統作為剛性負荷無法阻尼頻率變化，電網的負荷調節效應顯著降低，小功率擾動下極易引發頻率大幅波動。

1.2 風機潛在調頻能力

到2020年底，云南電網風電統調裝機容量為9 000 MW，冬季風電大發期日常正常出力波動在4 000～6 000 MW之間。可見風機大多處于中高轉速，轉子中儲存的動能量可觀，因此電網統調風機蘊藏著很大的潛在調頻能力。國內外的相關研究和試驗還表明[10-12]，風電的一次調頻響應滯后時間可以縮短到0.5～1.0 s，其屬于優質的快速頻率響應資源。

在系統日常方式安排時，云南電網水電機組盡管響應速度降低，但根據開機方式一次調頻向上備用一般在最大單機功率850 MW以上。直流FLC上調節量在2 500 MW以上，下調節容量在2 000 MW以上。因此在電網頻率低周問題下，通過附加轉子動能控制讓風電參與一次調頻，在系統遭受擾動初期，可以充分發揮其快速抑制頻率變化率、減小頻率最大偏差的優勢，彌補常規水電和火電機組一次調頻響應滯后時間長[13-15]和水電機組“水錘效應”的固有缺陷；在擾動中后期，可以與水火等常規同步機組或直流FLC協調配合，避免風機進入轉速恢復過程中引起的頻率二次跌落問題。

2 系統頻率仿真簡化模型

為了便于從與系統耦合的角度研究風電與常規同步機組及直流FLC相互作用對系統動態頻率的影響。本文在系統頻率響應(system frequency response，SFR)模型[16]上加入直流FLC模型和風機模型，建立了系統頻率仿真簡化模型。

2.1 系統模型

系統頻率仿真簡化模型如圖1所示。圖中：ΔPAL和ΔPDL分別為交流負荷和直流負荷功率增量；H和D分別為系統慣性時間常數和系統阻尼系數；Δf為系統頻率偏差，Δf=f-fref，f為系統頻率，fref為系統標準頻率；KH、KT分別為水電、火電的開機系數；ΔPH、ΔPT和ΔPW分別為水電、火電和風電有功出力增量；GH(s)和GT(s)分別為水電和火電機組頻率響應傳遞函數。圖1中的參數均以常規同步機組開機容量Ssyn(MW)為基準折算。

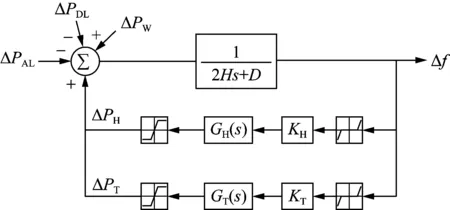
圖1 系統頻率仿真簡化模型Fig.1 Simplified model of system frequency simulation

水電開機系數KH和火電開機系數KT根據區域水火的大致開機比確定，KH和KT的關系為：

KT+KH=1

(1)

2.2 常規同步發電機頻率響應模型

根據文獻[17]，水電和火電頻率響應模型分別如圖2和圖3所示。

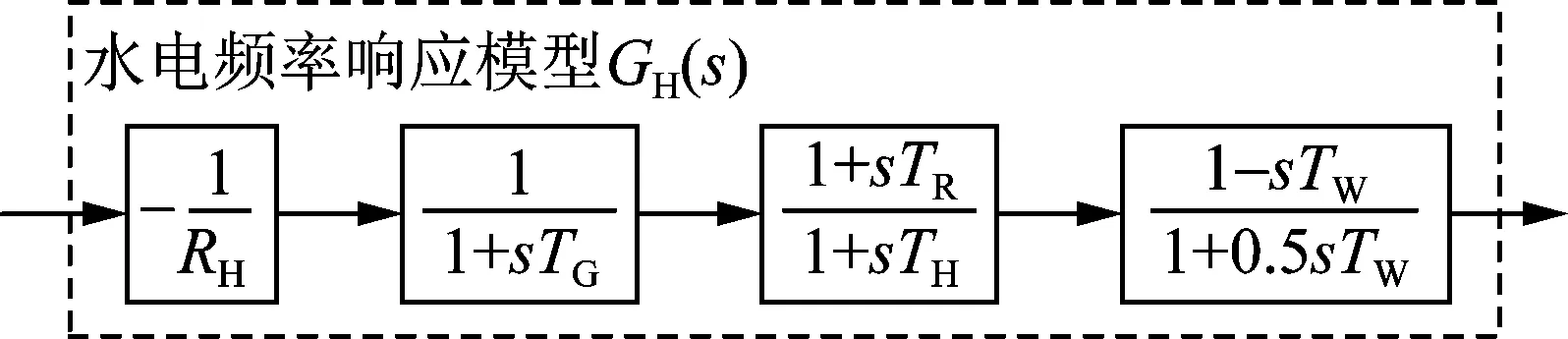
圖2 水電機組頻率響應模型Fig.2 Frequency response model of hydropower unit

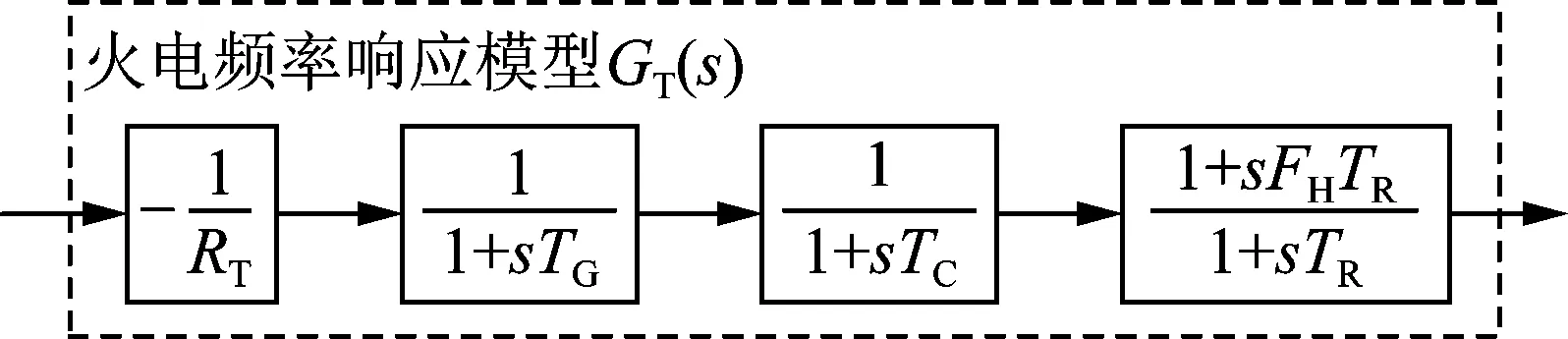
圖3 火電機組頻率響應模型Fig.3 Frequency response model of thermal power unit

水電頻率響應模型GH(s)中，RH、TG、TH、TR和TW分別為水電機組調差系數、調速器時間常數、暫態下垂時間常數、復位時間常數和水錘時間常數。

火電頻率響應模型GT(s)中，RT、TG、TC、TR和FH分別為火電調差系數、調速器時間常數、蒸汽容積時間常數、再熱時間常數和高壓缸比例系數。

2.3 直流FLC模型

云南電網的直流控制邏輯為：在正常情況下為恒定功率控制，在頻率越限情況下為頻差鎖定控制。本文直流FLC模型采用反向頻差復歸模型，反向頻差復歸模型的控制邏輯如圖4所示。

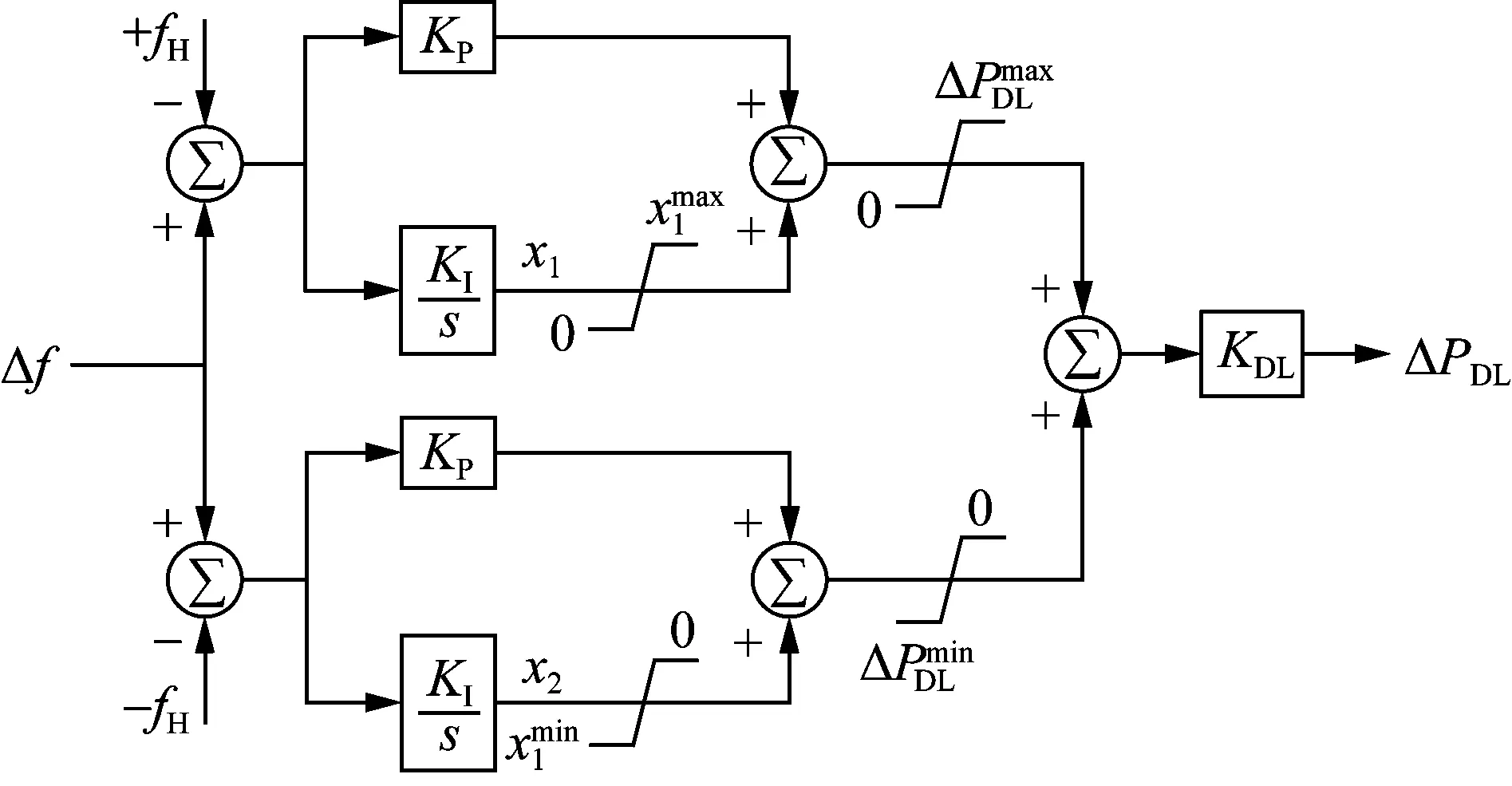
圖4 反向頻差復歸模型控制邏輯Fig.4 The model of FLC reverting under inverse frequency deviation

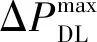
(2)

式中：SDL為直流系統容量。

2.4 風機模型

當前，云南電網統調風機幾乎都是雙饋異步風機。在研究頻率問題時，對于雙饋異步風機的簡化建模是保留風功率模型、軸系模型和最大功率跟蹤曲線控制，將風機變流器中間控制過程用低通濾波器等效[18-20]，附加了轉子動能控制、轉速保護模塊和轉速恢復模塊的風機模型如圖5所示。

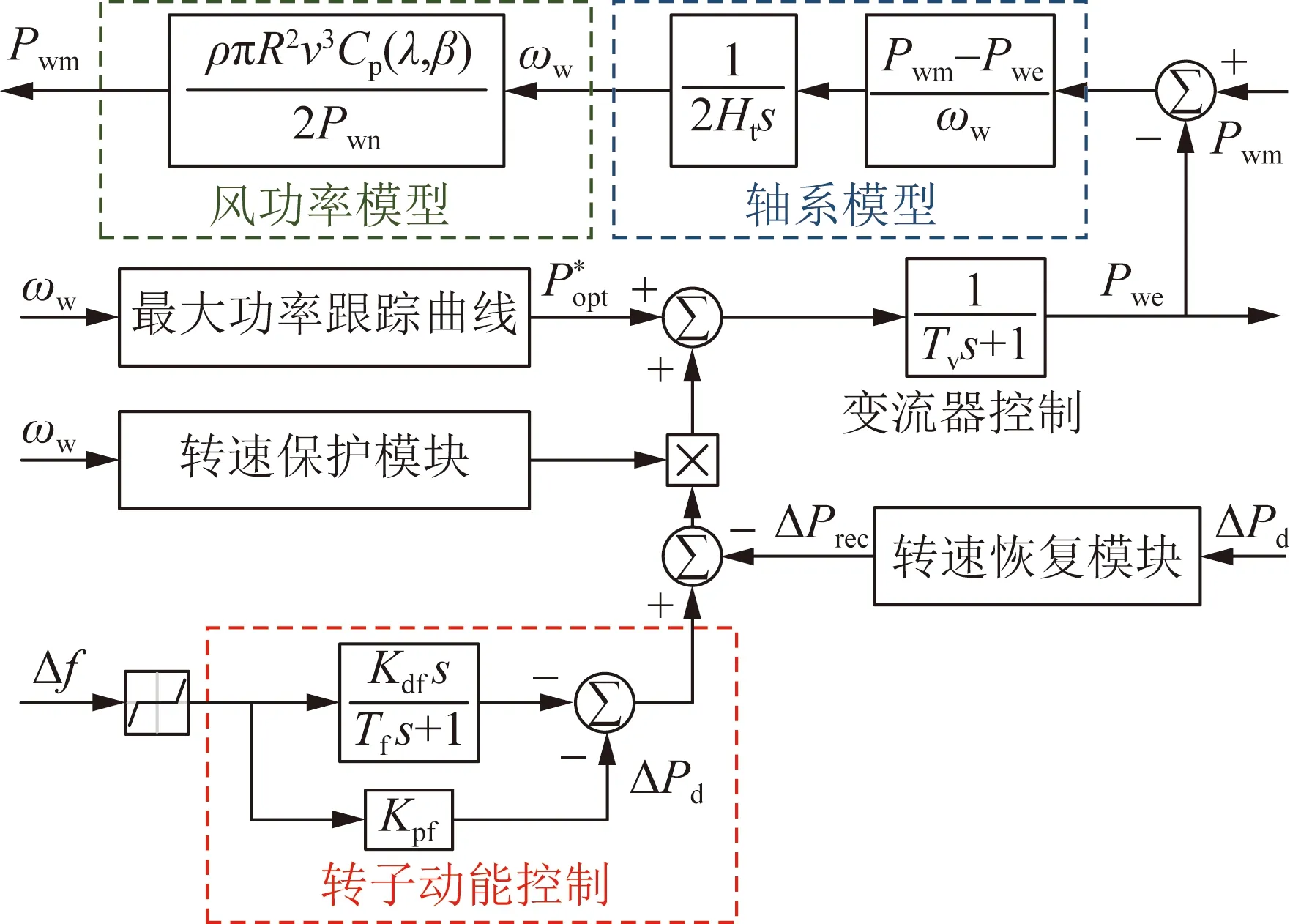
圖5 風機模型Fig.5 Model of a wind turbine

風功率模型中，ρ為空氣質量密度，kg/m3；R為風力機葉片半徑，m；v為風速，m/s；β為槳距角；λ為葉尖速比；Pwn為風機額定有功功率，MW；Cp(λ，β)為風能利用系數，其近似表達式為[20]：

(3)

(4)

(5)

式中：ωw為風力機轉速；ωwn為風力機額定轉速，rad/s。

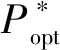
(6)

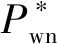
(7)

式中：Cpmax為最大風能利用系數；λopt為最佳葉尖速比。Cpmax和λopt可通過如下方式求得。

因為風機在MPPT區都是定槳距角運行，所以令Cp對λ求導得：

(8)

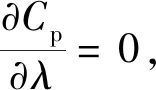
(9)

當β一定時，聯立式(3)和式(9)即可求取Cpmax，聯立式(4)和式(9)即可求取λopt。例如，當β=0時，Cpmax=0.438，λopt=6.32；當β=2時，Cpmax=0.402，λopt=7.3。

根據風況，風機在穩態情況下可能運行在MPPT區或恒轉速區，或是恒功率區。最大功率跟蹤曲線如圖6所示。

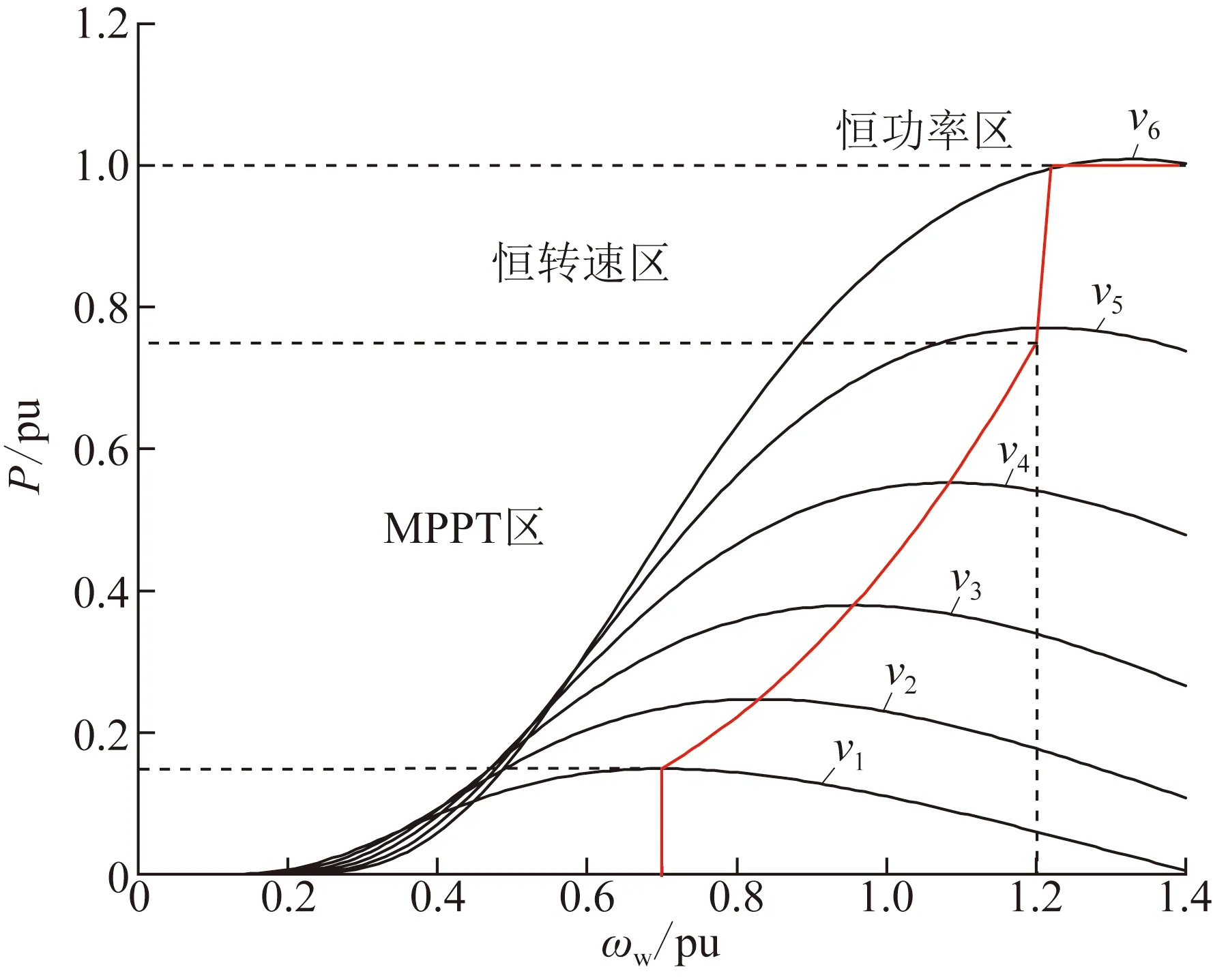
圖6 最大功率跟蹤曲線Fig.6 Curve of maximum power point tracking

轉子動能控制中，Kdf和Kpf分別為虛擬慣性控制系數和下垂控制系數；ΔPd為轉子動能控制環節輸出信號；Tf為虛擬慣性控制環節低通濾波器時間常數；Tv為變流器等效環節低通濾波器時間常數。

在系統頻率低周情況下，風機附加轉子動能控制參與系統頻率調整，當風力機轉速ωw低于最低轉速ωmin時，轉速保護模塊就會動作，將轉子動能控制和轉速恢復模塊切除，風機恢復最大功率追蹤曲線控制，從而瞬間給系統帶來負的功率沖擊，引起系統頻率二次跌落。

由于本文沒有在風機轉子動能控制下垂控制環節中設置高通濾波器，為避免風機調頻后影響系統的準穩態恢復頻率，本文采用補償功率的方法設置轉速恢復模塊[20]，補償功率ΔPrec表達式為：

ΔPrec=frec(t)ΔPd

(10)

式中：frec(t)為補償函數。

(11)

式中：trec,on為轉速恢復啟動時刻；Trec為補償函數時間常數。

風機電磁功率Pwe在轉速恢復模塊啟動后會先減小再增大。因此風機在轉速恢復過程中會不可避免地對系統頻率造成二次影響。需要說明的是，采用PI轉速恢復控制[19]也會給系統頻率造成二次影響。只不過PI轉速恢復控制是導致頻率短暫升高，補償功率的方式是導致頻率短暫降低。

風電有功出力增量ΔPW表達式為：

ΔPW=KW(Pwe-Pwe，0)

(12)

式中：Pwe,0為系統遭受擾動前風機的電磁功率；KW為風電開機系數。

(13)

式中：SW為風電開機容量，MW。

3 風機轉子動能控制參數設計

本文不考慮電網并網風機的機間差異和場間差異，將電網所有并網風機聚合為一臺風機，從風機與系統耦合的角度考慮風機轉子動能控制參數Kdf和Kpf的整定。

3.1 風機轉子動能控制參數設計思路

一般當風機出力超過自身額定的0.2時需要參與系統頻率調整[20]。則風機在MPPT控制下出力在0.2 pu對應自身轉速ωin可由式(14)求得。

(14)

聯立式(7)和式(14)，并代入λopt即可求得ωin對應的風機風速vin，vin為參與調頻風機對應風速下限，其表達式為：

(15)

由圖6可知，當系統出現頻率低周問題后，MPPT控制下出力在0.2 pu的風機可向上調量充足，但轉速可變化范圍較小。如果不考慮風機死區和低通濾波器的作用，由圖5可知，當風機采用轉子動能控制參與系統頻率調整時，風機的轉子運動方程為：

(16)

進一步，假設調頻初期風機機械功率的變化等于電磁功率的變化，由式(16)化簡得：

(17)

則由式(17)可知，系統頻率低周問題越嚴重，在擾動初期風機的轉速變化就越快，變化量就越大。如果參與調頻的風電機組都采用同樣的輔助調頻參數Kdf和Kpf，處在低轉速的風機在系統嚴重故障下相對容易觸發轉速保護動作。此外，當風機運行在恒轉速區并接近恒功率區時，風機轉速可變化范圍大，但風機向上可調節量較小；只有中高風速下運行的風電機組有著較大的轉速變化范圍和可觀的上調節量。

因此可見，同一套轉子動能控制參數并不同時適用于任一風速運行下的風電機組，且也不能發揮各風電機組的調頻能力。雖然在實際工程中，不會讓風機根據風速變化采用變參數的方式參與系統頻率調整。但在參數整定時可以研究不同風速下風機的調頻能力，其轉子動能控制參數設置范圍，為風電機組采用統一的轉子動能控制參數提供參考。

對于區域電網來講，應根據系統的運行方式及其最大可信事故的變化調整風機的轉子動能控制參數，參與調頻的風機的風速應在vin和vn之間。

對于投有直流FLC功能的云南電網而言，風機在系統頻率低周問題下的功能應該是在保證不會引起頻率二次跌落的同時減小系統頻率最大偏差和改善直流FLC的動作情況。

3.2 風機轉子動能控制參數整定方法

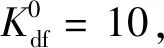
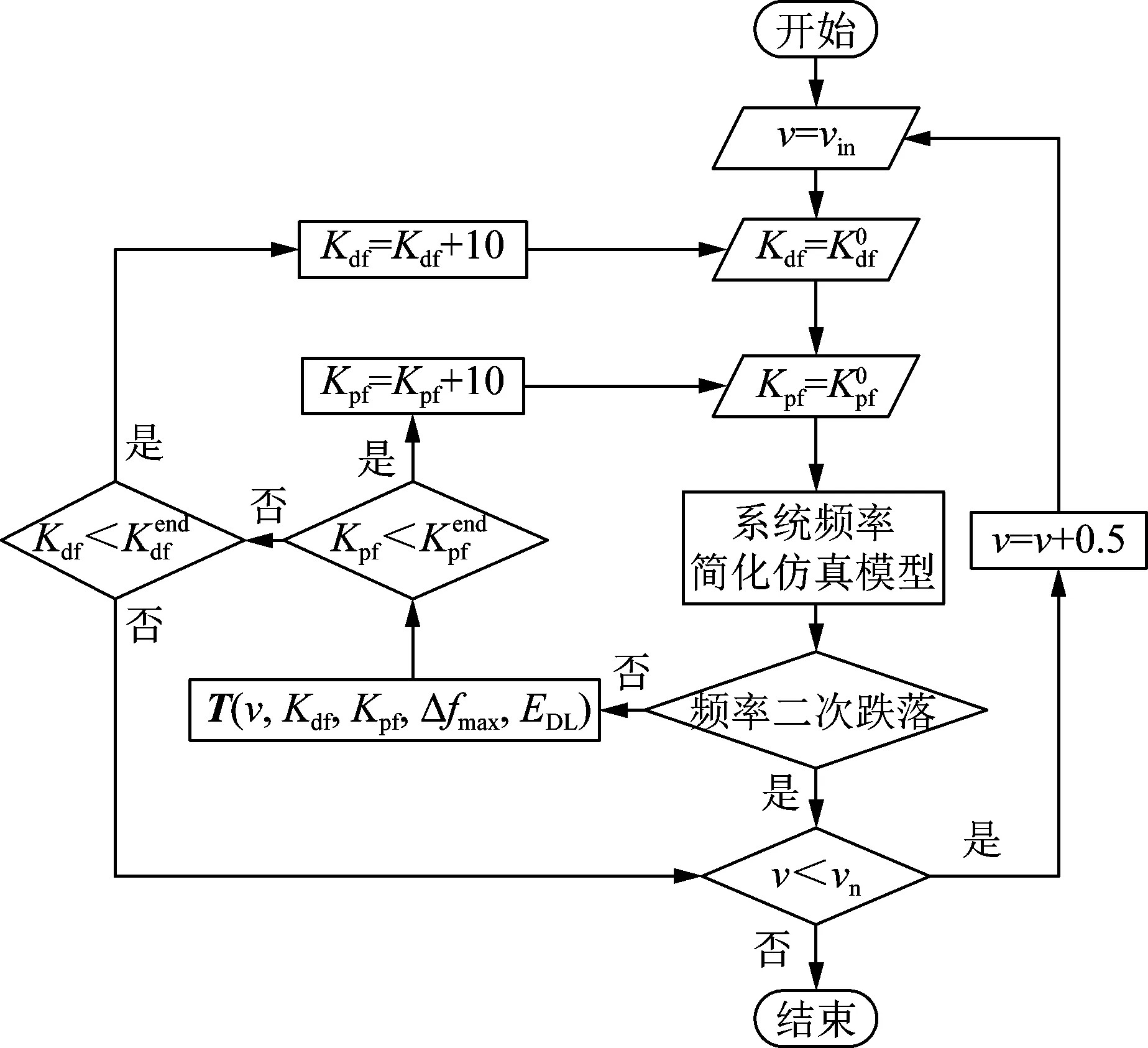
圖7 風機參數整定流程Fig.7 Setting process of wind turbine parameters

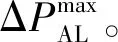
因為同步機的開機容量Ssyn和風電開機容量SW已經確定，這里忽略風電載荷比變化對于同步機開機規模的擠占影響。

步驟2：通過圖7給出的參數整定流程，確定風速在vin和vn之間不會出現頻率二次跌落的Kdf和Kpf組合，將v、Kdf、Kpf、Δfmax和EDL存入到矩陣T中。其中，Δfmax為頻率最大偏差；EDL為直流負荷功率增量積分，表示為：

(18)

步驟3：依據矩陣T，根據Δfmax和EDL隨著v、Kdf和Kpf的變化關系，分析不同風速下風機的虛擬慣性控制系數Kdf和下垂控制系數Kpf取值規律并對比其調頻能力，結合頻率、直流FLC和風機的動態過程進一步確定不同風速下風機的Kdf和Kpf參數取值范圍。

綜上，在系統某一運行方式下對應風機在不同風速下的Kdf和Kpf參數取值范圍得以確定，為后續風機采用統一的轉子動能控制參數提供參考。

4 算例分析

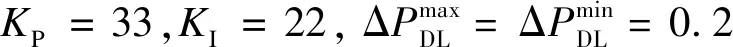
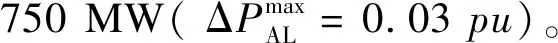
4.1 虛擬慣性控制系數取值規律以及各風速下風機調頻能力對比分析

為分析虛擬慣性控制系數Kdf的取值規律以及同一Kdf取值下風機在不同風速下的調頻能力，圖8給出了風機運行在MPPT區，Kpf=10時，不同Kdf取值對應的最大頻率偏差和直流負荷功率增量積分絕對值曲線。

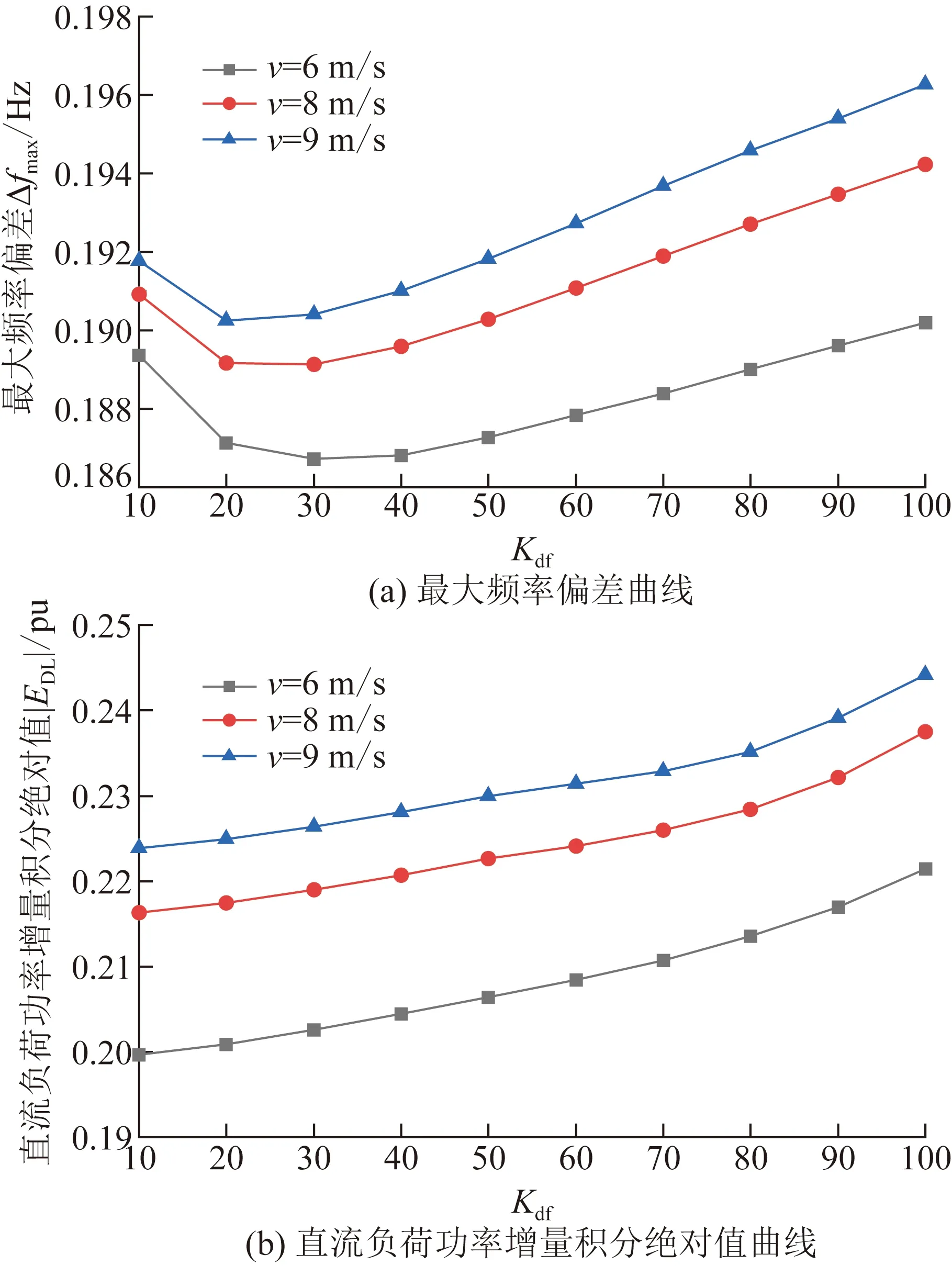
圖8 不同Kdf下Δfmax和|EDL|曲線Fig.8 Δfmax and |EDL|curves under different Kdf

由圖8可知，同一Kpf和Kdf取值下，風機改善系統的頻率最大偏差和直流FLC的動作量的能力隨著風速增大而減小。由圖8(a)可知，在某一特定風速下，風機改善頻率最大偏差的能力會隨著Kdf的增大先增大后減小；風機改善直流FLC動作量的能力會隨著Kdf的增大不斷減小。

圖9給出了風速在9 m/s、Kpf=10時，不同Kdf取值下系統的頻率曲線、風電有功出力增量曲線和直流負荷功率增量絕對值曲線。由圖9可知，Kdf越大，除了會降低風機改善系統頻率最大偏差和直流FLC動作量的能力，還會讓系統頻率在進入直流FLC死區后出現嚴重超調，并隨著風電有功出力跌落又導致頻率出現嚴重反調，嚴重情況下會導致頻率再次超過直流FLC動作死區，引起直流FLC再次動作。

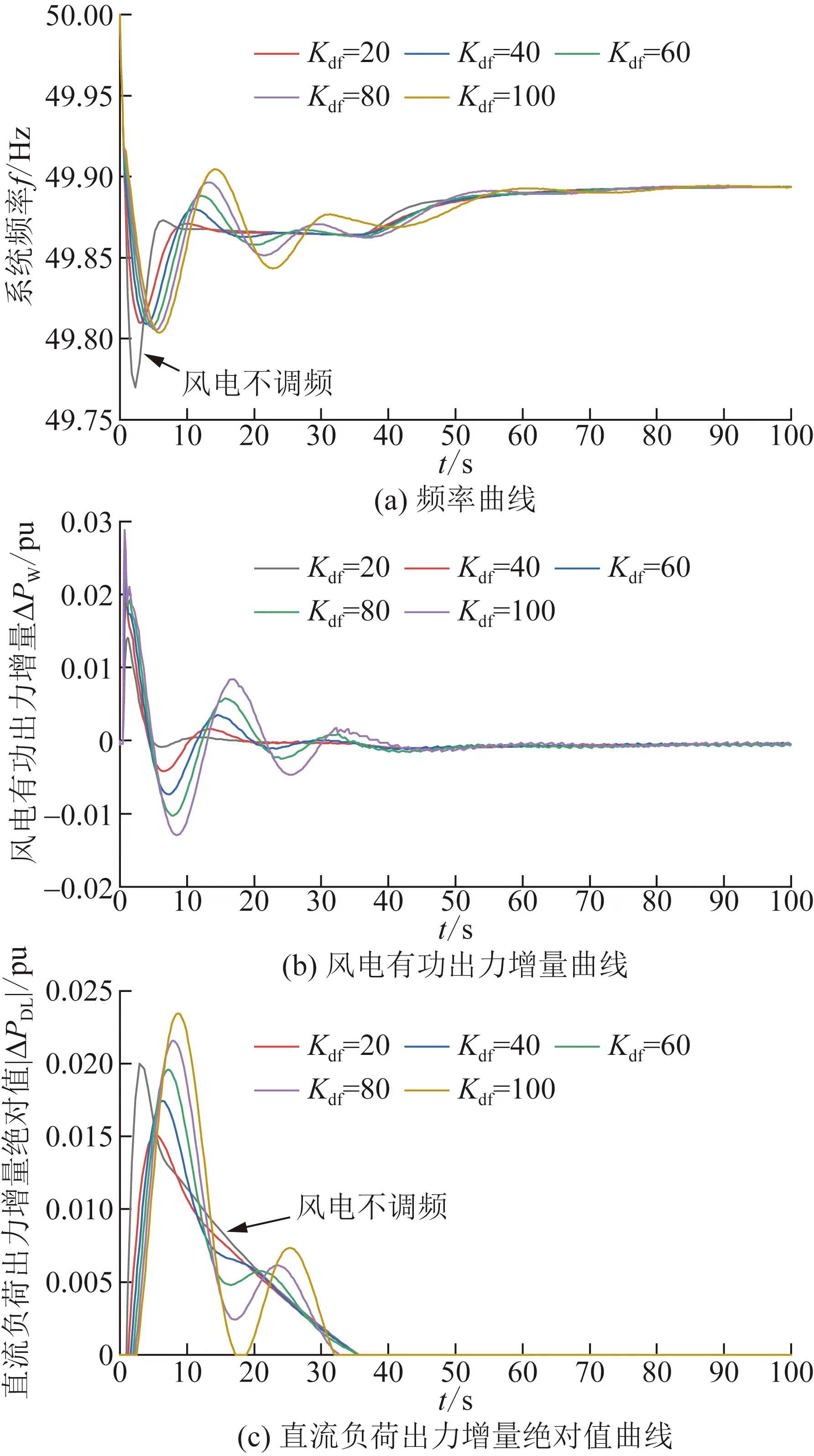
圖9 v=9 m/s時不同Kdf下頻率f、風電有功出力增量ΔPW和直流負荷出力增量絕對值|ΔPDL|曲線Fig.9 f，ΔPW and |ΔPDL|curves under different Kdf at v=9 m/s

因此，在系統小負荷運行方式下，對于投入直流FLC功能的異步互聯送端高比例水電系統，當風電機組采用統一的轉子動能控制參數參與系統頻率調整時，虛擬慣性控制系數Kdf建議取值在10～20之間。

4.2 下垂控制系數取值規律以及各風速下風機調頻能力對比分析

為分析下垂控制系數Kpf的取值規律以及同一Kpf取值下風機在不同風速下的調頻能力，圖10給出了風機風速在vin和vn(6～9 m/s為MPPT區，9.5 ～10.4 m/s為恒轉速區)，Kdf=10時，不同Kpf取值對應的最大頻率偏差和直流負荷功率增量積分絕對值曲線。

同樣由圖10可知，同一Kdf和Kpf取值下，當風機運行在MPPT區時，風機改善頻率最大偏差和直流FLC動作量的能力都隨著風速增大而減小，差距相對較小；而當風機運行在恒轉速區時，風機改善頻率最大偏差和直流FLC動作量的能力雖然也都隨著風速增大而減小，但差距相對較大。

由圖10可知，當風機運行在MPPT區和靠近MPPT區的恒轉速區時，增大Kpf顯著增強了風電改善頻率最大偏差和直流FLC動作量的能力，但Kpf到一定值時，增大Kpf對于提升風機改善系統頻率最大偏差和直流FLC動作量的能力幾乎沒有改變。此外，由圖10還可知，靠近恒功率區運行的風機幾乎沒有調頻能力。當風機運行在MPPT區時，在系統小負荷運行方式下，如果風機參與系統頻率調整，能將系統最大N-1故障下的頻率最大偏差縮小至少0.08 Hz。

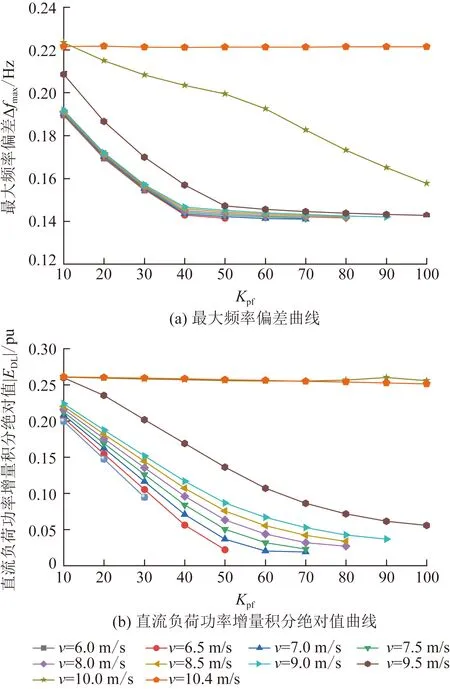
圖10 不同Kpf下Δfmax和|EDL|曲線Fig.10 Δfmax and |EDL|curves under different Kpf

圖11給出了Kdf=10，風機在不同風速不同Kpf取值下參與系統頻率調整后的系統頻率曲線和風電增出力增量曲線。由圖11可知，低風速(例如v=6 m/s)機組受到轉速限制，Kpf取值過大會引起轉速保護動作，導致風電出力瞬間跌落，從而給系統頻率帶來二次跌落問題；當風速偏高(例如v=9 m/s和10 m/s)時，Kpf取值過大，會嚴重影響頻率恢復到準穩態頻率的時間，因為本算例的轉速恢復啟動時刻trec,on設置為100 s，所以圖11(a)v=9 m/s對應頻率曲線會出現較為明顯的頻率跌落現象；受出力幅值限制，靠近恒功率區運行(例如v=10.4 m/s)的機組受機組限幅影響，所以調頻效果不佳。

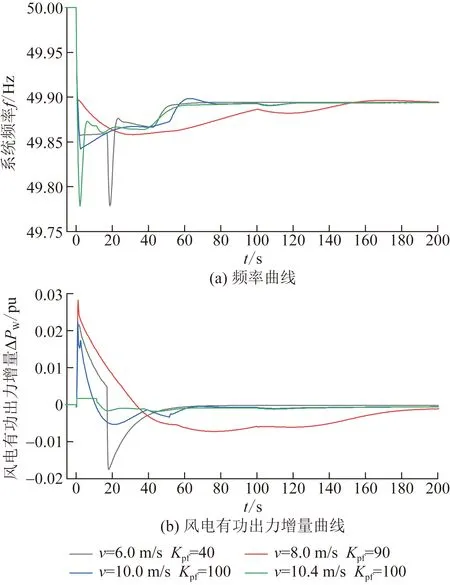
圖11 不同風速v、不同Kpf下頻率f和風電有功出力量ΔPW曲線Fig.11 f and ΔPW curves under different v and Kpf

由上述分析可知，在系統小負荷運行方式下，對于投入直流FLC功能的異步互聯送端高比例水電系統，當風電機組采用統一的轉子動能控制參數參與系統頻率調整時，下垂控制系數Kpf取值受低風速機組取值影響，取值不要超過30。

5 結 論

1)對于投入直流FLC功能的異步互聯送端高比例水電系統，風機采用轉子動能控制能夠很好地降低電網頻率峰值越限風險，改善直流FLC動作情況。

2)對于投入直流FLC功能的異步互聯送端高比例水電系統，增大虛擬慣性控制系數Kdf，不利于改善頻率最大偏差，會導致系統頻率在到達準穩態頻率前出現嚴重的超調和反調現象，帶來頻率二次跌落。

3)下垂控制系數Kpf是改善頻率最大偏差和減少直流FLC動作量的關鍵。同等Kdf和Kpf參數取值情況下，風電機組改善頻率最大偏差和直流FLC動作量的能力都隨著風速增大而減小，當風機運行在MPPT區時，其調頻能力差距相對較小；當風機運行在恒轉速區時，其調頻能力差距相對較大；靠近恒功率區運行的機組幾乎沒有調頻能力。

4)低風速機組Kpf取值受轉速約束限制，取值過大會導致轉速保護動作帶來頻率二次跌落問題；中高風速機組Kpf取值過大雖然不會引起頻率二次跌落問題，但嚴重影響頻率到達準穩態頻率的時間；增大Kpf到一定值時，繼續增大Kpf不能提升風機改善頻率最大偏差和直流FLC動作情況的能力。