基于互補濾波的汽車姿態數據采集系統研究*

張新宇

(遼寧省交通高等專科學校軌道交通工程系,遼寧 沈陽 110122)

隨著汽車行業的快速發展,汽車監控系統越來越受到重視,汽車監控系統一方面可以監督駕駛員的駕駛行為,另一方面,也可以在發生事故后,進行事故回放,判定事故責任,保護駕駛人員的合法權利。

近年來,廣泛應用于無人機領域的MEMS 傳感器,由于其體積小、成本低、集成度高、精度高,逐步在汽車監控領域得到了應用。但是MEMS 傳感器由于自身的特點,存在難以克服的噪聲誤差,因此,必須采取相應的算法,來消除噪聲誤差。劉軍等[1]中使用六軸傳感器,實現汽車運動姿態測量,采用卡爾曼濾波算法消除誤差,由于重力加速度的存在,加速度計無法修正陀螺儀的航向角,卡爾曼濾波算法比較復雜。王京等[2]中使用三軸加速度計,采用改進的遺傳神經網絡算法消除誤差,實現汽車姿態測量,但是三軸加速度計無法計算航向角,算法也比較復雜。曹景偉等[3]使用陀螺儀和加速度計,利用卡爾曼濾波算法將MEMS 陀螺儀和加速度計輸出的數據進行濾波融合。但沒有使用磁強計數據,無法修正航向角,無法解算出準確的全方位姿態角。且算法比較復雜。李超[4]使用陀螺儀、加速度計和磁強計,主要研究線性加速度的干擾,誤差方程采用卡爾曼濾波算法。算法比較復雜。王贇贇[5]使用三軸加速度數據、三軸角速度數據和三軸地磁數據,采用一種基于粒子濾波的條件式姿態解算算法,獲得姿態角,采用非線性擴展卡爾曼濾波進行數據融合。算法比較復雜。

因此設計了一種基于互補濾波的汽車姿態數據采集系統,采用互補濾波數據融合算法,解算出全方位的姿態數據,為監控汽車的運行狀態提供一種新的手段。

1 慣性導航原理

慣性導航是一種自主式定位方法,它是利用加速度計、陀螺儀和磁力計實時測量物體的線運動、角運動以及其他外界的運動信息,根據運動特性和慣性微分方程,并在給定初始條件下,推算運動物體的位置、速度和運動姿態信息。

運動姿態的表示方法有方向余弦、四元數和歐拉角。歐拉角在求解姿態時存在奇點,不能用于全姿態的解算；方向余弦可用于全姿態的解算,但是計算量較大,不能滿足實時性要求。四元數計算量小,無奇點,可以滿足汽車運動過程中姿態的實時解算。因此采用四元數來進行姿態解算。

由于使用陀螺儀、加速度計和磁力計單獨計算姿態信息,都有各自存在的無法規避的物理缺陷:使用陀螺儀測量值計算,積分過程中容易產生較大的累積誤差,使用加速度計測量值計算,無法分離加速度測量值中的重力分量與運動分量,使用磁力計測量時,容易受到環境中磁場干擾的影響,這3 種誤差在使用過程中是無法預先消除的,所以就必須要使用相應的數據處理方式來最大限度上消除單一傳感器產生的誤差。

陀螺儀和加速度計的姿態信息成互補性,可以采用濾波的方法進行加權平均,取得最好的估計結果。常用的方法有卡爾曼濾波和互補濾波。

卡爾曼濾波[6]是一種對系統狀態進行遞推最優估計的算法,它使用觀測信息以及前一時刻的最優估計值作為系統輸入,來估計該時刻的狀態量。卡爾曼濾波的權重有一個逐步收斂的過程,計算量較大,而且需要對待測變量的誤差模型有一個準確的估計。

互補濾波法[7]是根據不同傳感器的各自特性,即加速度計/磁力計具有高頻噪聲(需要低通濾波),陀螺儀具有低頻噪聲(需要高通濾波),通過高通或低通濾波器來濾波,然后再進行組合來進行數據的融合。互補濾波的權重固定,不需要對誤差模型做過多估計,計算量較小,因此采取互補濾波算法。

2 系統總體設計

汽車姿態數據采集系統分為車載單元和上位機單元。車載單元主要由嵌入式處理器、運動傳感器、北斗模塊和存儲模塊組成。處理器將運動傳感器采集到的九軸數據進行融合解算,得到有效的姿態信息,結合北斗模塊定位信息和時間信息,以固定格式保存到存儲模塊中。

3 系統硬件設計

本系統采用基于ARM Cortex -M4 內核的STM32F407ZGT6 高性能處理器,其時鐘頻率達到168 MHz,功耗低,具有更快的模數轉換速度、更強大的輸入/輸出端口。傳感器采用六軸MPU6050 和三軸磁力計 HMC5883L。定位模塊采用北斗ATGM336H。存儲模塊用來把數據保存到U 盤中。如圖1 所示。

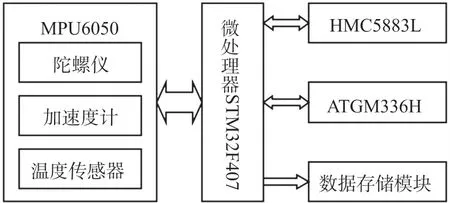
圖1 系統硬件框圖

4 汽車姿態數據解算

慣性器件都有各自的缺點和局限性,單一使用任何傳感器,都無法得到有效準確的姿態信息。因此,需要利用多個傳感器之間存在性質互補的特點,將多個傳感器數據融合到一個單一的、最優的姿態估計中[8],從而得到最準確的姿態數據。

數據解算流程圖如圖2 所示。

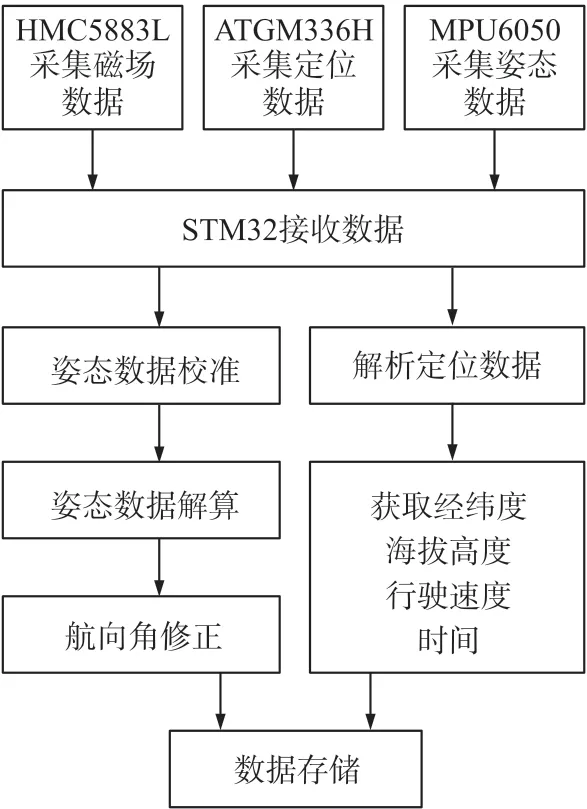
圖2 程序設計流程圖

4.1 九軸數據校準

三軸加速度計、三軸陀螺儀、三軸磁力計的讀數都會有偏移的現象,數據并不是圍繞著靜止的工作點擺動,因此,有必要校準九軸數據[9]。

三軸陀螺儀的校準是相對簡單的工作,只要找到擺動的數據圍繞的中心點。在靜止狀態時,陀螺儀的X軸、Y軸和Z軸讀數理論上應為0,但往往會存在偏移。

通過計算機串口讀取一段靜止時的三軸陀螺儀讀數,將這三組讀數用統計均值的方式獲取偏移量,每次的讀數都減去偏移量就可以得到校準后的數據了。

加速度計的校準需要將設備置于水平、堅固的平面上。加速度計的X軸和Y軸的理論值應為0,加速度計的Z軸的理論值應為-16 384(假設加速度計設定為2 gn,g的加速度的讀數應為最大值-32 768的一半)。

通過計算機串口讀取一段時間的三軸加速度數值,由于加速度計的X軸和Y軸的理論值應為0,這2 個讀數偏移量可以用統計均值的方法求得。加速度計的Z軸統計偏移量時,每次讀數都需要加上16 384,再進行統計均值計算。之后每次都減去偏移量就可得到比較準確的三軸加速度值。

磁力計的校準[10-12],如果磁力計平放著繞Z軸旋轉一周,讀回的X軸和Y軸2 個軸的數據組成的點,理論上會形成一個圓,而實際上卻是一個橢圓,并且中心點不在原點,此時使用航向角公式算出的角度是不準的,如果想用航向角公式的話,需要把這個偏移的橢圓校正成中心點在原點的正圓。校準的輸出可以根據下面的方法來計算:

通過計算機串口收集磁力計被旋轉360°后的數據。對采集到的數據進行分析,找到磁力計X軸、Y軸以及Z軸的最大值和最小值,xmax,xmin,ymax,ymin,zmax,zmin。

于是可以得到X軸的偏移值為:

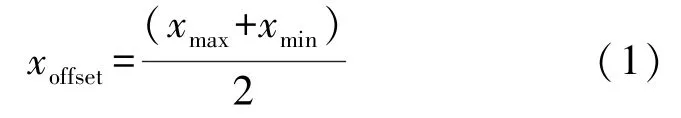
因為只需要方向,所以可以設X軸的比例系數xgain為1。

Y軸的偏移值為:

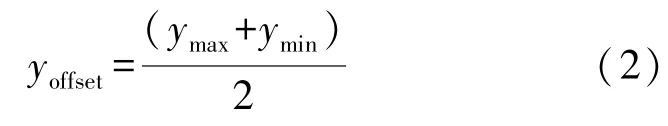
Y軸的比例系數可以由下式計算。

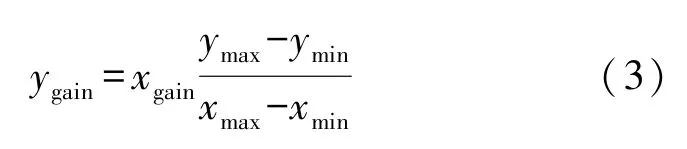
Z軸的偏移值為:

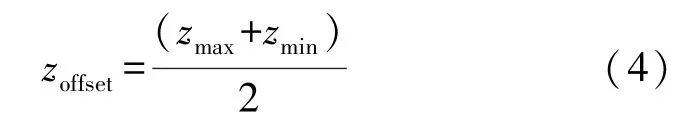
Z軸的比例系數可以由下式計算。

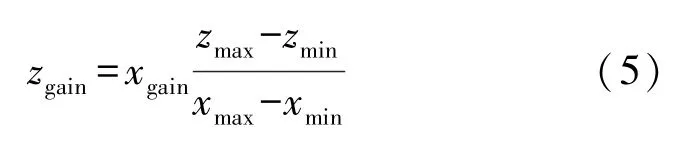
磁力計可以由下式校準。

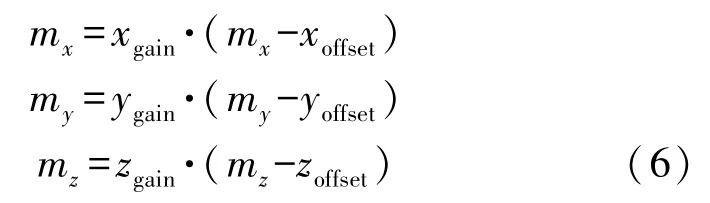
4.2 九軸姿態解算

陀螺儀可獲得角速度,通過積分可獲得角度,但隨時間累積,積分漂移誤差會越來越大,陀螺儀響應速度快,表現為低頻特性,誤差隨時間累積。

加速度計對載體的加速度敏感,動態響應較慢,表現為高頻特性,測量傾斜角時,短時間誤差較大[13]。

通過互補濾波將陀螺儀和加速度計的優點結合起來[14],可以在低頻段和高頻段得到較好的信號,有效提高姿態輸出精度。

標準重力加速度gb從導航坐標系n系轉換到載體坐標系b系中的四元數表示的矩陣為:

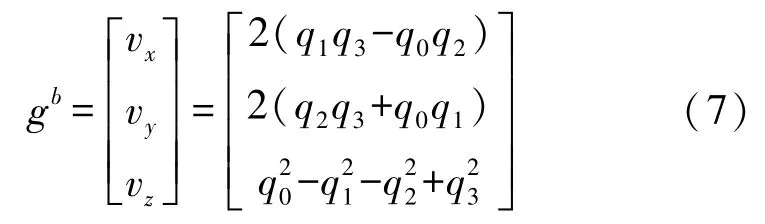
式中:vX、vY、vZ是標準重力加速度gb的X軸、Y軸、Z軸分量。q0、q1、q2、q3是四元數中的實數分量。

加速度計測得的三軸加速度ab在b系中的矩陣表示為:

式中:ax、ay、az是三軸加速度ab在X軸、Y軸、Z軸分量。

gb和ab都是b系的向量,經過歸一化處理后,模長為1,gb和ab向量叉乘的大小僅與sinθ有關,當角度很小時,叉乘結果可以近似于角度成正比。這個結果可以作為給陀螺儀的校正補償值。公式為:

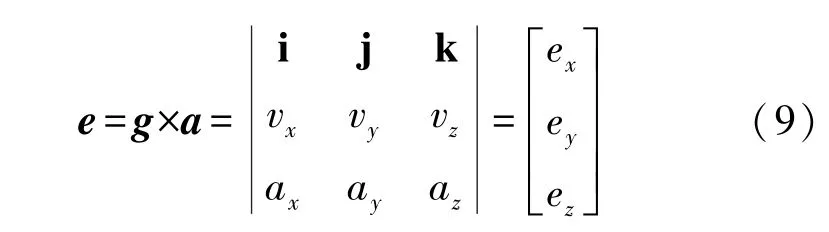
利用PI 控制器進行互補濾波處理,消除偏移誤差。

PI 控制的公式為:

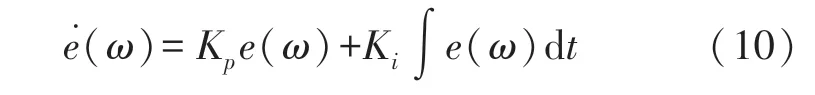
式中:ω是陀螺儀輸出的角速度,是陀螺儀的校正補償值。

只要誤差存在,PI 控制器就會持續作用[15],直到誤差為0。控制的效果取決于P 和I 的值,分別對應于比例控制和積分控制的參數。PI 控制器參數獲取的具體方法為,先設定積分控制系數Ki為0,將系統變為純比例調節,然后將比例控制系數Kp值由零開始逐步增大,直到系統出現振蕩,再反過來調節將Kp值逐漸減小,直到系統振蕩消失,記錄當前的比例控制系數Kp值；當比例控制系數值確定后,設定一個比較大的積分時間常數Ti,逐漸減小積分時間常數,直到系統出現振蕩,再增大積分時間常數Ti,直到系統振蕩消失,記錄當前的積分時間常數Ti值,積分控制系數Ki就等于Kp除以Ti。

將補償值加到三軸陀螺儀輸出的數據上進行數據修正、融合[16]。

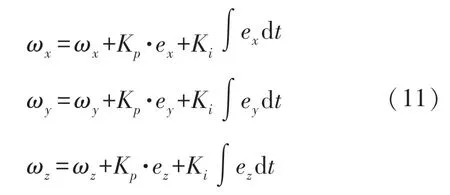
將融合后的陀螺儀數據通過四元數微分方程轉化為四元數輸出。

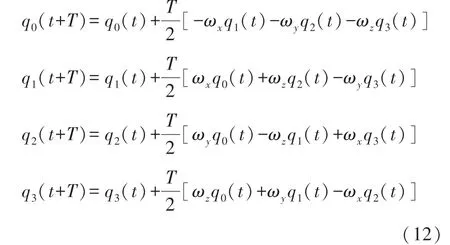
式中:T為采樣周期。

將得到的四元數轉化為姿態角。

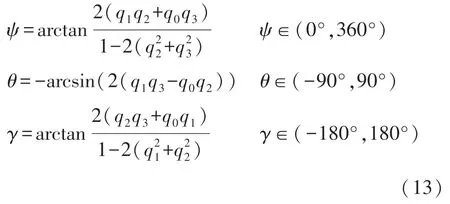
互補濾波解算法流程如圖3 所示:

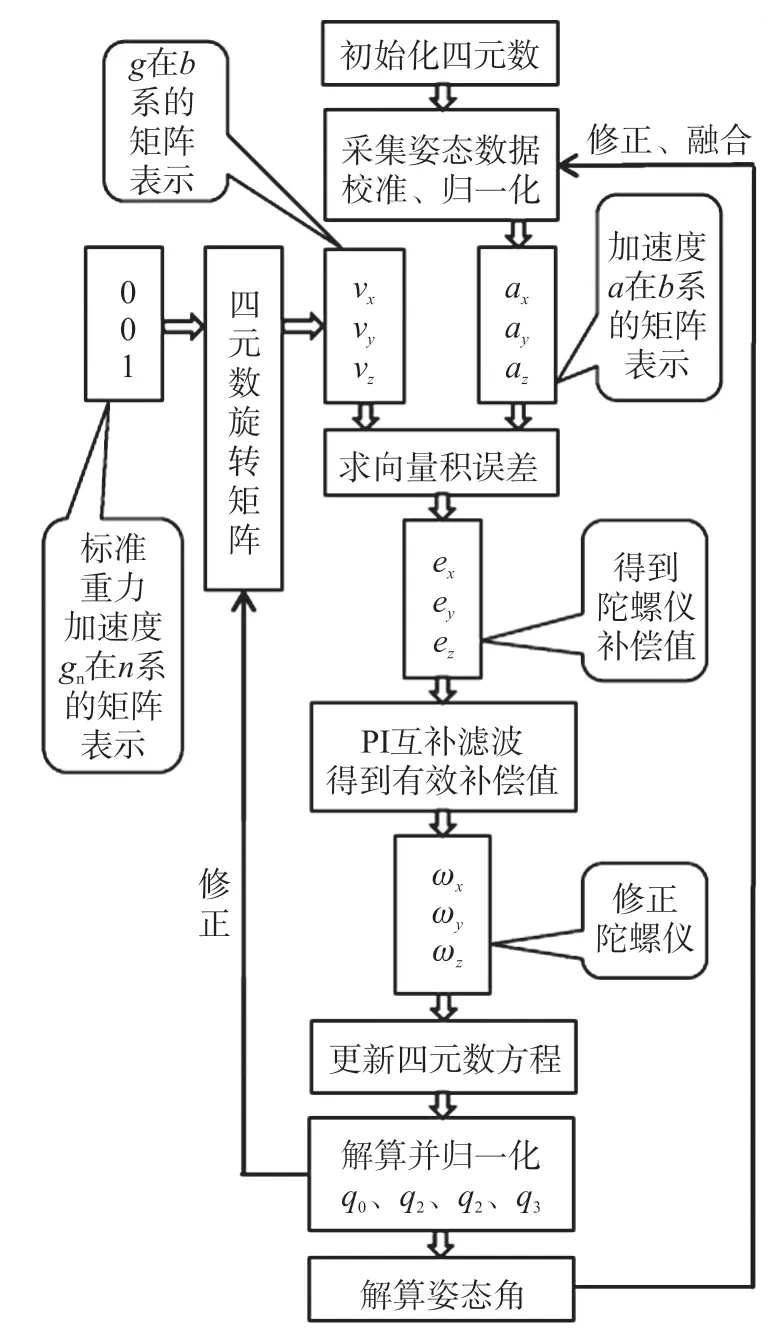
圖3 互補濾波解算法流程圖

4.3 航向角修正

上面的互補濾波法因為沒有參考量,無法計算出當前的航向角γ的絕對角度,只能得到航向角γ的變化量,也就是陀螺儀的Z軸的角速度。可以通過對陀螺儀Z軸角速度進行積分,來計算當前航向角γ。由于測量精度以及溫度影響的問題,并且,隨著時間的推移,計算值會產生累積誤差,長時間后就完全失去了意義。

加速度計可以取得與地球重力相關的橫滾和俯仰方向的姿態信息,可以用來修正陀螺儀的橫滾角和俯仰角,但是加速度計無法測量重力方向(即Z軸方向)的旋轉,無法計算出航向角,無法修正陀螺儀的航向角。因此需要加入磁力計HMC5883L 來解決這個問題,得到3 個軸的準確姿態信息。

水平放置時航向角可由下式得到:

式中:MY和MX是磁力計的Y軸和X軸分量。

單獨使用磁力計時,無法保證磁力計水平放置,導致測量的航向角有較大誤差,通常利用加速度計來修正磁力計的傾斜角。

非水平放置時通過MPU6050 獲得俯仰角(ψ)和翻滾角(θ)對航向角進行傾斜角補償,公式如下:

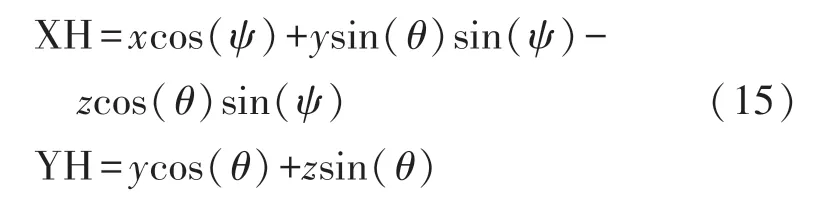
非水平放置時航向角公式為:

5 試驗驗證

將本系統固定在汽車上,在汽車運行過程中,采集汽車運行姿態數據。上位機采用MATLAB 的GUI 功能進行設計,通過讀取系統中存儲的以時間命名的文本文件數據,其中存儲著時間、加速度、角速度、磁向量、溫度、海拔高度、行駛速度等數據信息。在上位機界面上以曲線的形式把汽車的運行軌跡描繪出來。經過對比,能夠真實地反映出汽車的運行狀態。

圖4 所示是以時間為X軸,三軸加速度為Y軸的曲線圖。

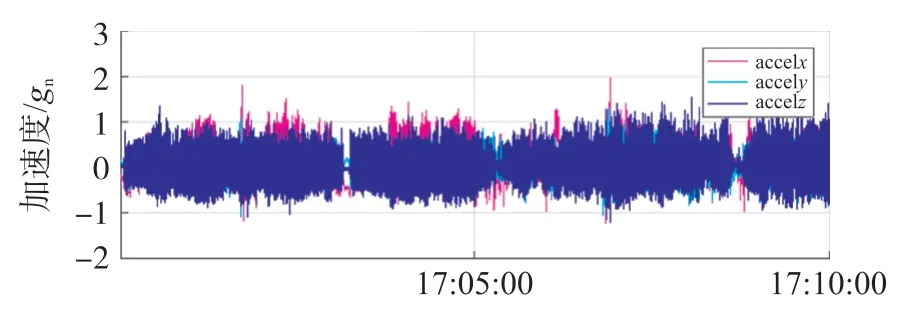
圖4 三軸加速度曲線圖

圖5 所示是以時間為X軸,三軸角速度為Y軸的曲線圖。

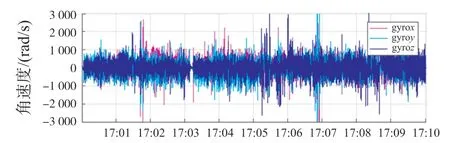
圖5 三軸角速度曲線圖

圖6 所示是以時間為X軸,三軸磁向量為Y軸的曲線圖。

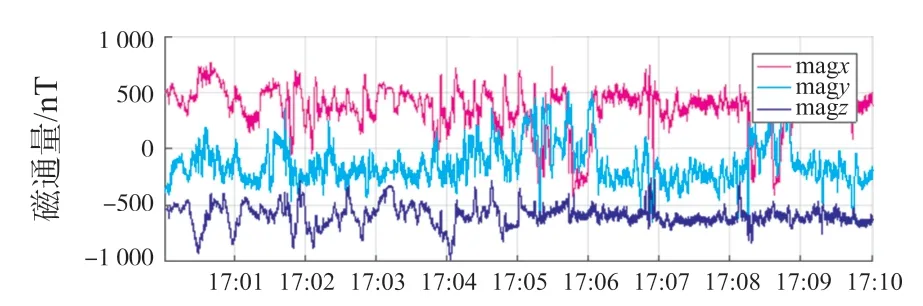
圖6 三軸磁向量曲線圖

圖7 所示是以時間為X軸,分別以翻滾角(θ)、俯仰角(ψ)、航向角(γ)為Y軸的曲線圖。

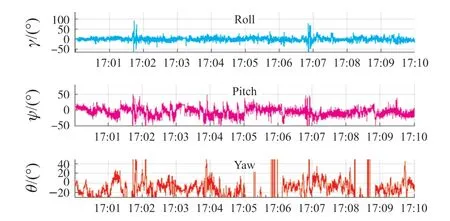
圖7 姿態變換曲線圖

對于姿態的變換,是將解算出來的俯仰角、翻滾角和航向角通過計算轉換為在圖上顯示的點的變換。

首先計算航向角γ,即xOy平面中的轉動,只需要讓三角形的3 個點分別在下圖中顯示的大圓和小圓上即可。如圖8 所示。

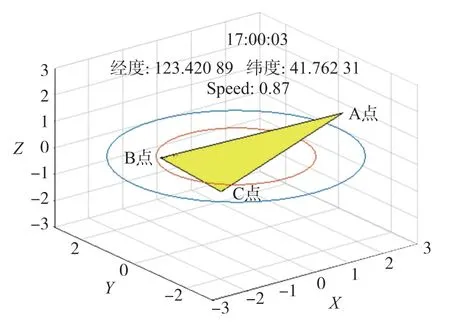
圖8 姿態變換三維圖

對于俯仰角ψ,規定以坐標(0,0,0)的點進行旋轉,即2 個圓的圓心,因此計算俯仰角ψ需要在xOz平面內計算,通過公式sin(ψ)就可以計算出A、B、C3 個點分別在Z軸上的坐標,同時在A點變換后,其相對應的X軸、Y軸變換公式是cos(ψ)。

對于翻滾角θ,需要計算B點和C點分別在Z軸上的坐標,因為這個三角形是繞著(0,0,0)轉的,并不是繞著BC的中點旋轉,因而無法利用BC的長度乘以sin(θ)計算獲得。所以需要通過圓心作一條直線和BC線平行,假設其與AC交與F點,與AB交與E點。如圖9 所示。

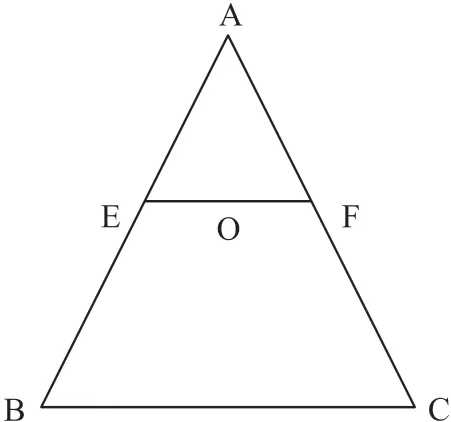
圖9 姿態變換計算三角形

無論ψ和θ如何轉動,OF都是位于xOy平面內的,利用公式sin(θ)OF就可以得到F點在Z軸的變化,從而通過等比計算就可以得到C點在Z軸的變化,B點的變化和C點是一樣的,只是方向相反,將BC的坐標在xOy平面利用公式cos(θ)得到,再進行縮放就可以得到三角形的三個坐標點。

6 結論

使用三軸加速度計、三軸陀螺儀、三軸磁力計采集姿態數據,采用統計均值法,進行九軸姿態數據校準,有效地解決了零點漂移,簡單易行；采用互補濾波法,合理調整PI 參數,進行數據融合,較之卡爾曼濾波,計算量小,更適合工程實現；針對加速度計無法修正航向角的問題,采用加速度計修正磁力計的水平問題,再用磁力計修正航向角。彌補了六軸傳感器無法修正航向角的不足,全方位修正了姿態角。經過實際車輛測試,能夠真實地反映出汽車的運行狀態。為監控汽車的運行狀態提供了一種更簡單、更實用的手段。