網絡環境下“數學分析”混合式教學設計研究
——以連續函數的概念為例

陶玉杰，段麗芬，程亞煥，于梅菊

“數學分析”是數學與應用數學專業重要的專業基礎課，也是后繼課程學習的基礎，具有極強的理論性、邏輯性和系統性［1］.而數學概念是數學分析知識體系中重要的一環，是深入學習、理解一切的基礎，因此做好概念教學是十分必要的.在以往的概念教學中，通常是直接給出定義，這種教學方式硬性灌輸，忽略了學生認知形成過程和參與體驗，使得原本就抽象的概念更加枯燥乏味難以理解，不能有效激發學生進一步學習的興趣.因此，在進行概念教學時，要充分利用現代信息技術，借助超星學習通平臺，大膽嘗試、精心設計教學過程，采取線上線下混合式教學模式，從生活現象、生活實際出發，利用問題驅動法讓學生直接參與定義得出的過程，親自嘗試用數學語言進行刻畫，這樣學生對定義的理解一定會更深刻，有益于后繼內容的學習.

1 教學?內容分析

1.1 內容分析

連續函數是“數學分析”中著重討論的一類函數，連續函數概念是學生進入連續函數性質學習的第一道門檻，由于定義很抽象，初學的學生在理解上會有一定的難度.本節主要的學習內容為：

（1）函數在x0點連續的定義；

（2）函數在x0點連續的等價形式；

（3）定義的應用.

1.2 學情分析

“數學分析”的授課對象為數學與應用數學專業大一學生，經過一個階段的學習，學生已經對極限思想有了充分的了解；由于剛剛步入大學校門，學生還未完全適應大學的學習生活，沒有養成良好的學習習慣，課前自主預習和課后復習沒有成為學習常態，課后只是為了完成作業而做作業；學生的學習基礎參差不齊，差異性較大，有的學生對抽象的數學分析不感興趣.

1.3 目標分析

知識目標：從生活現象出發，通過問題的設置使學生了解連續性概念的實際背景，建構對連續性的認知基礎，引導學生思考，給出連續性概念，掌握函數在一點連續的精確定義及等價形式.

能力目標：通過學習，培養學生從具體到抽象、發現和轉化的思維能力；培養學生課前、課后自主學習能力及課上合作探究能力.

思想目標：通過學生親自參與知識建構，激發學生學習的興趣，使學生真正理解連續性定義，并能認識到在生活中，凡事不能急于求成，必須遵循事物原本的規律.

1.4 重點難點分析

（1）利用問題驅動法引導學生探索連續性的本質.

（2）通過小組合作，師生共同討論完善對連續性的理解.

（3）通過典型例題進一步加深和拓展對概念的理解，掌握極限存在與函數在一點處連續的區別與聯系.

2 教學設計策略

“數學分析”中的概念具有抽象性，不易理解，所以在教學過程中依據先行組織者策略，打破傳統的教學模式，積極采用現代信息技術，通過超星學習通平臺將線上線下混合式教學融入傳統教學模式中，以學生為中心，提高課堂效率.在課堂實施過程中，采用問題驅動教學方法，借助小視頻、PPT等輔以講授法、小組討論等形式完成對函數連續性概念的感知、提煉、形成、鞏固和應用，提高學生對概念的理解和運用能力.

3 教學過程設計

“數學分析”中連續函數的概念與高中階段學習的概念相比較，“數學分析”中連續函數的定義不僅僅是定性的描述，而重要的是要從定性描述中抽象出定量的描述.如何從具體教學中抽象出連續函數的概念，引導學生明晰其各種等價形式是連續函數概念教學的重點.本節內容以課前（線上）—課中（線下）—課后（線上）為主線，利用超星學習通完成教學任務.

3.1 課前（線上）準備

課前，通過線上超星學習通平臺發布學習任務，讓學生了解學習目標.第一步，教師線上發布學習資源，比如課件、小視頻等，小視頻中主要給出植物的生長過程、潺潺的流水、溫度的變化、舞者手中的飄帶等生動的畫面，讓學生從鮮活的畫面中去感知連續性，增強學習欲望，促使學生進行在線預習；第二步，布置查閱任務：通過所發布的小視頻，結合生活實際，讓學生再查找一些與連續相關的生活現象，加深對連續性的認知.連續來源于生活，反過來又怎么樣應用于生活中呢？引導學生查閱連續性的應用，在查閱過程中讓學生感受到抽象的數學與生活是息息相關的，激發他們繼續學習的興趣；第三步，教師與學生進行線上互動交流，收集學生課前預習中所遇到的疑難問題，以備課堂上進行探究釋疑.課前的線上教學是學生自主完成的學習活動，是上好一節課的關鍵.

3.2 課中（線下）課堂實施

線上學習活動是作為線下教學的補充，根據線上學習反饋，完成知識的鞏固、拓展和提升.在這一環節中，通過問題驅動法完成連續函數的概念教學，重點是抽象出連續函數定義及其等價形式，按課前回顧、問題引入、分組探究、歸納總結、課堂小結這五個環節進行展開.

（1）課前回顧.教師首先檢驗線上自主學習效果，設計幾個關于函數極限問題作為課前小測，這為后面解答函數極限與函數的連續之間的關系做準備.利用學習通統計小測結果，可以快速掌握預習情況.其次讓學生代表展示其查閱的與連續性相關的生活現象，讓學生快速融入課堂氣氛之中.

（2）問題引入.首先，借助學生查閱的生活現象提出問題：“一提到連續，你會想到什么詞匯？”學生通過預習肯定會答出：“連綿不斷”.教師可補充說明連續描述的就是連綿不斷的現象.

其次，通過與連續相關的生活現象設計問題：“我手里有一根斷開的繩子，那么怎么樣把他們連接起來，使兩段繩子看起來是連綿不斷的一根繩子呢？”這個問題比較簡單，很容易引導學生得出簡單的方法，就是將斷開的繩子湊到同一個點，然后用膠水粘住即可，這樣斷開的繩子便連接起來.

最后，引導學生從這一現象出發嘗試用數學符號進行刻畫，進一步抽象出函數在一點處連續的定義.將斷開的繩子湊到一起，也就是這兩段繩子從兩側向同一個點湊近，在數學上解釋這一現象可以用左右極限刻畫.這兩段繩子的斷點湊在一起并用膠水粘住，在數學上描述就是這一點處左右極限存在且相等，而且還要等于函數在這一點處的函數值，這就給出了函數在一點連續的定義，用數學符號表述如下：

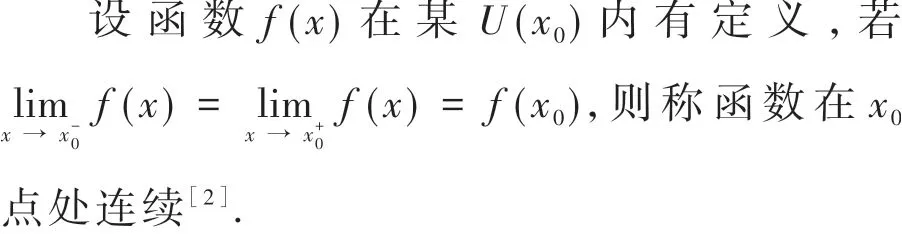
（3）分組探究.在給出函數f(x)在x0點連續的定義后，設計以下4個層層遞進的問題讓學生進行分組合作探究，通過探究性問題可實現知識的遷移.

探究1：針對上述抽象出來的f(x)在x0點連續的定義，你是否能用其他形式來表達這個定義？

探究2：函數f(x)在x0點連續的定義是用極限定義的，那么函數f(x)在x0點極限存在和f(x)在x0點連續之間有什么聯系呢？

探究3：函數f(x)在區間I上連續如何定義？

探究4：怎樣證明函數f(x)在區間I上連續？

在小組合作探究的時候，教師可以與各小組進行交流，了解同學們的掌握情況.幫助他們盡快實現知識的遷移.

（4）歸納總結.經過小組合作探究，讓各組學生代表進行歸納總結，小組之間也可以進行互評，教師在此期間進行補充、糾錯，最后對所提問題進行總結.

對于探究問題1：設函數f(x)在某U(x0)內有定義，若滿足下列條件之一，函數f(x)在x0點連續.

對于探究問題2：函數f(x)在x0點極限存在，則f(x)在x0點不一定連續，反之函數f(x)在x0點連續，則函數f(x)在x0點極限存在.即函數f(x)在x0點極限存在是f(x)在x0點連續的必要條件.

對于探究問題3：函數f(x)在區間I上的每一點都連續，則f(x)為I上的連續函數.對于閉區間或半開半閉區間的端點，函數在這些端點連續是指左連續或右連續.

對于探究問題4：若要證明函數f(x)在區間I上連續，依據定義，只需證明區間內每一點均連續，即?x0∈I，證明f(x)在x0點連續即可.若區間I是閉區間或半開半閉區間，還需證明在端點處左連續或右連續.

（5）課堂小結.教師對整個教學過程中學生的表現進行點評，對所學知識點做進一步梳理，強調重點、難點，引導學生進行課后學習.

3.3 課后（線上）提升

通過超星學習通平臺，教師布置課后任務，引導學生再次進行深入的學習和應用.課后任務要有層次，以滿足不同層次學生的需求，使學生在課后得到進一步提升.

教師可以在平臺上批閱學生提交的作業，通過作業情況掌握學生的學習情況，對于個別接受較差的同學或接受能力強的同學可以進行個別輔導.

在(0,1)內任何無理點處都連續，任何有理點處都不連續.

4 教學效果

線上線下混合式教學有效拓展了教學時空，極大地豐富了教學資源，充分體現了學生的主體地位，最大限度實現了預期教學目的.課前通過學習通平臺向學生發布自學任務和學習資料，為課上討論做好前期準備；課上從植物的生長、潺潺流水、溫度的變化、舞者手中的飄帶等生活現象入手，讓學生感受到抽象的連續函數概念有著豐富生動的生活背景.課上通過斷開的繩子設計問題，引導學生給出函數在一點處連續的定義，并用數學符號進行刻畫，使學生對抽象的概念有了直觀認識.再通過精心設計的問題，讓學生分組進行討論并匯報討論結果，教師進行補充、糾錯，使學生完成知識的遷移，使相關認知得到升華；課后布置階梯式練習，滿足各個層次學生的需要，真正做到全員參與學習“一個也不能少”.整個教學過程層層遞進，環環相扣，內容一氣呵成，通過學生親歷定義的給出過程，激發了學生的學習興趣，函數連續的概念教學在匠心獨運的教學設計和意趣盎然的教學環節中完美收官.

“信息化教學手段引入數學課堂，有助于走出一支粉筆、一塊黑板、一本書的傳統課堂教學模式”［3］.線上線下混合式教學模式避免了傳統教學中“填鴨式”式教學方法的枯燥與單一，課堂上，通過層層遞進的問題，讓學生分組討論，教師從旁輔助、糾錯，克服了線上教學模式中教師與學生溝通不便的弊端，實現了教師與學生、學生與學生之間的互動，這不僅能夠發揮教師的引領作用，又能充分發揮學生的主觀能動性與創造性.信息化教學已成為現代教育發展的必然趨勢［4?5］.但是要想實現高效的線上線下相結合的課堂教學，教師必須要掌握現代信息技術，具備較高的業務水平，這對教師提出了極大的挑戰.本文以“函數的連續性概念”為例，充分發揮了線上的優勢，通過超星學習通平臺，學生自主學習，打破了時間和空間的界限，線下采用分組討論研究式學習，真正調動了學生學習的積極性，構建了以學生為主體的線上線下相結合的課堂教學方式，但如何在“數學分析”教學中全面實踐線上線下混合式教學模式還需要更多的探索.