高速列車的自適應容錯跟蹤控制
徐傳芳
(大連交通大學 自動化與電氣工程學院,遼寧 大連 116028)*
列車自動駕駛是未來高速鐵路列車運行的發展趨勢,是軌道交通領域的研究熱點之一.對于高速列車自動駕駛技術的研究主要集中在兩個方面:目標速度和位移曲線的優化以及對目標速度和位移優化曲線的跟蹤控制[1-2].目前,在綜合考慮安全性、準時性、節能以及乘坐舒適性等性能指標,計算目標速度和位移優化曲線方面已經取得了豐碩的研究成果[3-7].在得到速度和位移優化曲線后,如何通過設計高性能的列車跟蹤控制算法,實現列車對優化速度和位移曲線的精確跟蹤,就成為達到列車運行控制各項性能指標要求的關鍵,否則目標速度和位移曲線的優化也就失去了意義.
為此,很多學者對列車的速度與位移跟蹤控制進行了研究[8-12].然而,文獻[8-9]所提出的列車控制器依賴于部分列車模型參數.而實際上,列車模型參數難以精確獲知,比如,列車質量會受到上下車旅客及其所攜帶行李的影響;基本阻力系數雖然可以通過風洞實驗和實際運營所積累的數據獲知,但在列車實際運行中,它們會隨著線路狀況、天氣、列車質量等變化.為了應對列車模型參數不確定性的影響,文獻[10-12]通過引入自適應控制技術,實現了不依賴于列車模型參數的精確速度和位移跟蹤控制.然而,文獻[10-12]并沒有考慮執行器故障問題.列車在長時間、大距離、高速度運行中,執行機構不可避免地會發生電氣故障或機械故障,出現部分失效甚至完全失效,這就需要系統具有自動應對此類故障的能力.被動容錯控制不需要故障檢測與診斷設備,不需要重組控制器[13-14],易于實現.然而,目前關于執行器故障下列車被動容錯跟蹤控制的研究成果還不夠豐富.
本文考慮列車模型參數的不確定性和執行器效率部分損失故障,設計了列車的自適應容錯跟蹤控制器,并基于Lyapunov穩定性理論和仿真實驗證明和驗證了所提出控制器的有效性.
1 高速列車動力學模型
列車單質點模型受力分析簡單,在模擬列車的運行效果時,具有實時、準確、快速的優點,在計算效率和精度方面具有較高的水平[15], 適合應用于要求快速、實時的場合,是列車運行控制中最常用的模型[16].其受力分析如圖1所示.
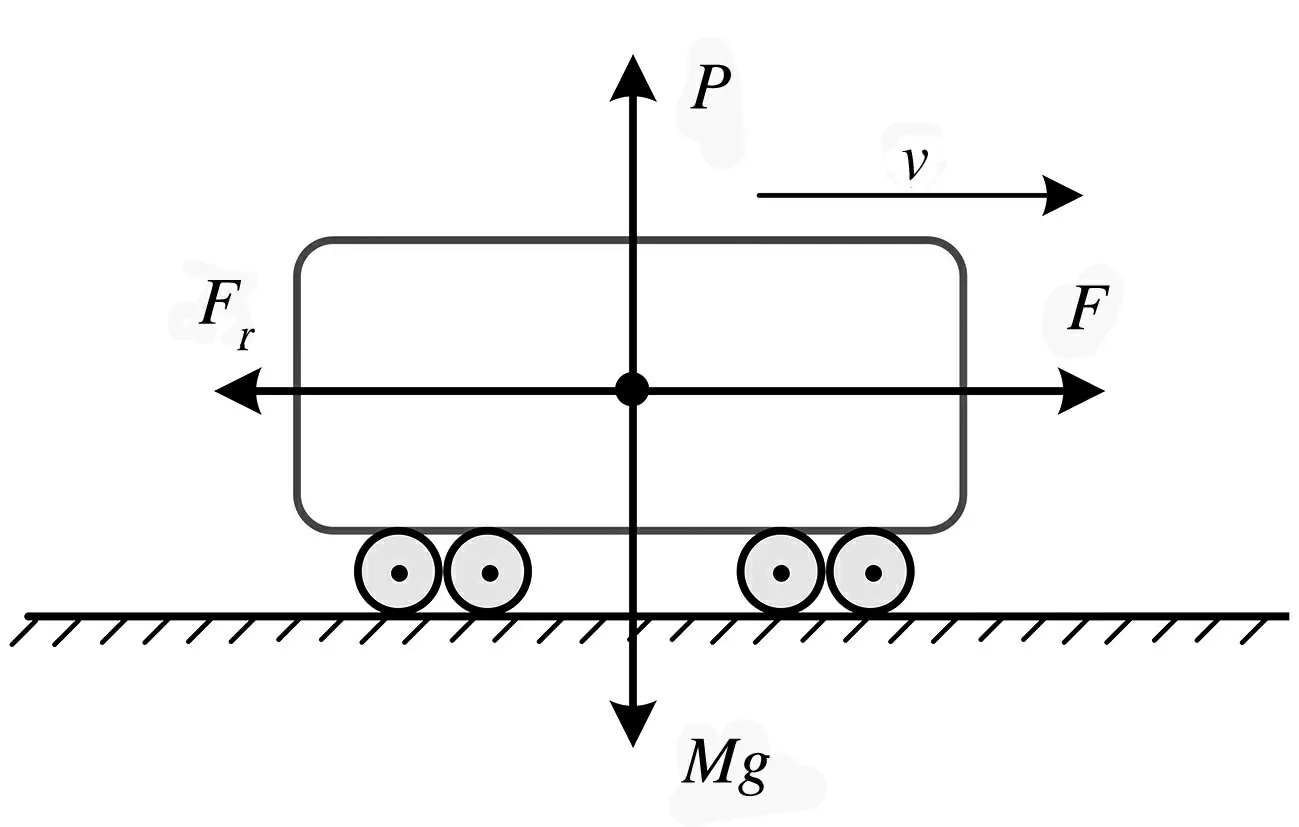
圖1 列車單質點模型
圖中,M為列車的總重量;g為重力加速度;v為列車的速度;F為列車牽引力或列車制動力,其中,在列車牽引階段,F為列車牽引力,其方向與列車運行方向相同,在列車制動階段,F為列車制動力,其方向與列車運行方向相反;Fr為作用在列車上的總運行阻力.
根據牛頓第二定律,列車單質點動態特性可以描述為
(1)
本文只考慮列車受到基本阻力情況.列車基本阻力主要由車輛部件和車輛表面與空氣之間的摩擦,以及車輪與鋼軌間的摩擦與沖擊等產生,目前常采用經典的Davis方程來描述,即
Fr=a0+a1v+a2v2
(2)
式中,a0、a1、a2為正實數,一般可以從風洞試驗和實際運營所積累的數據中獲知,但實際運行中難以精確獲知.
列車在線路上運行時,由于頻繁的執行控制任務,執行機構不可避免地會出現故障,如電機過熱或匝間短路故障、牽引變流器過電流故障、機械驅動器磨損故障等.這些故障可被分為卡死故障、失控故障、浮式故障和執行器效率損失故障等[17].其中,執行器故障比其他部件故障發生概率更高[18].本文針對執行器效率部分損失故障展開討論.
執行器效率部分損失故障意味著執行器效率的部分損失,對于單質點列車動力學模型,可將此類故障看作一個整體[19].因此,發生執行器效率損失故障的執行器實際輸出可描述為:
F′=kcF
(3)
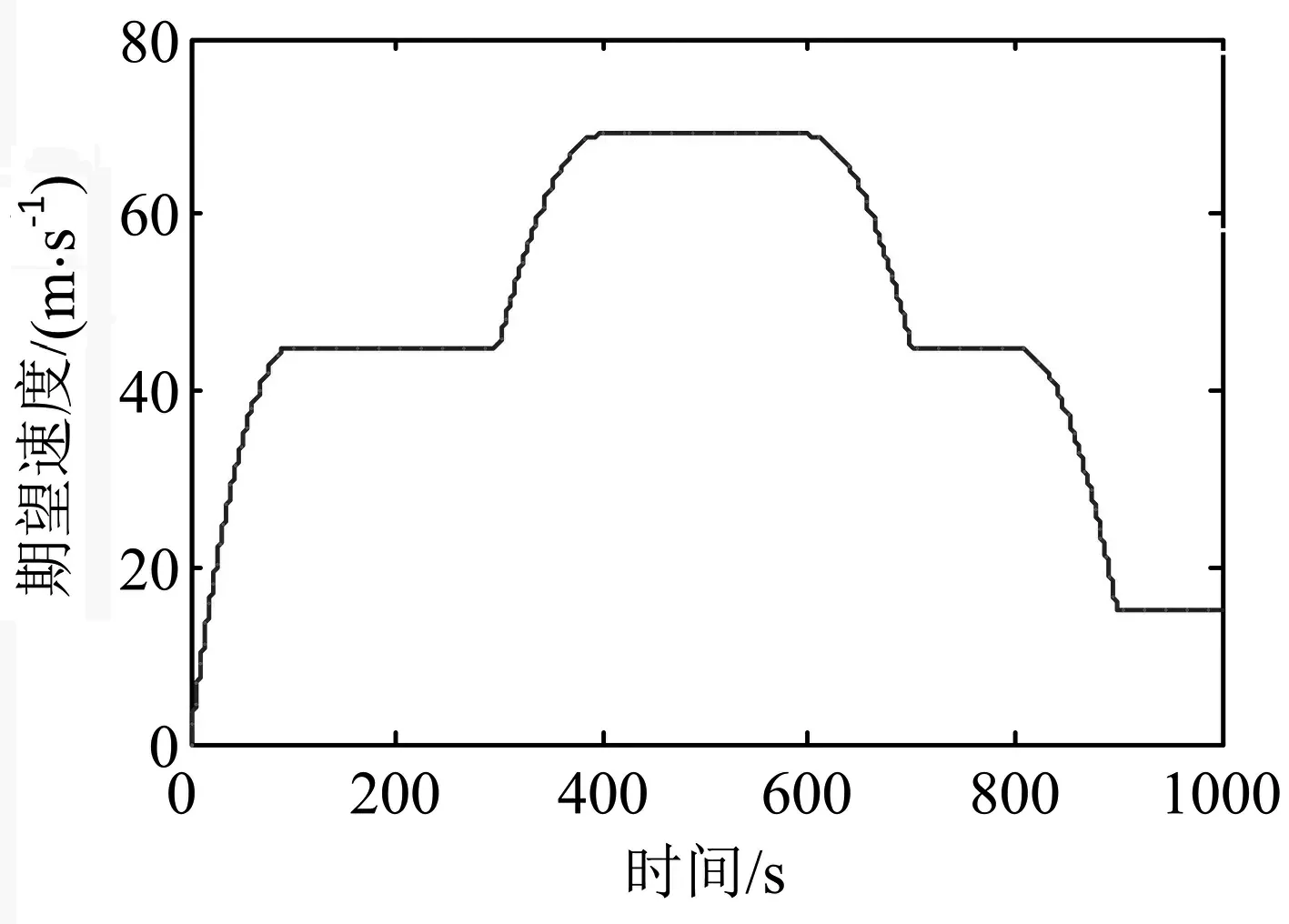
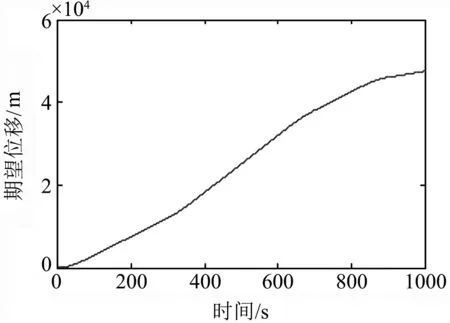
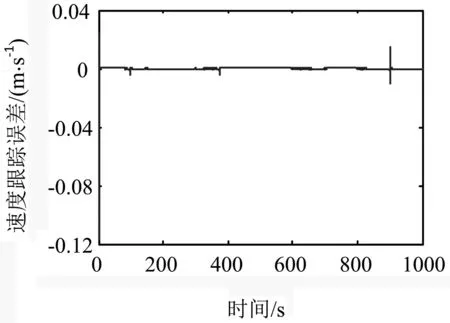
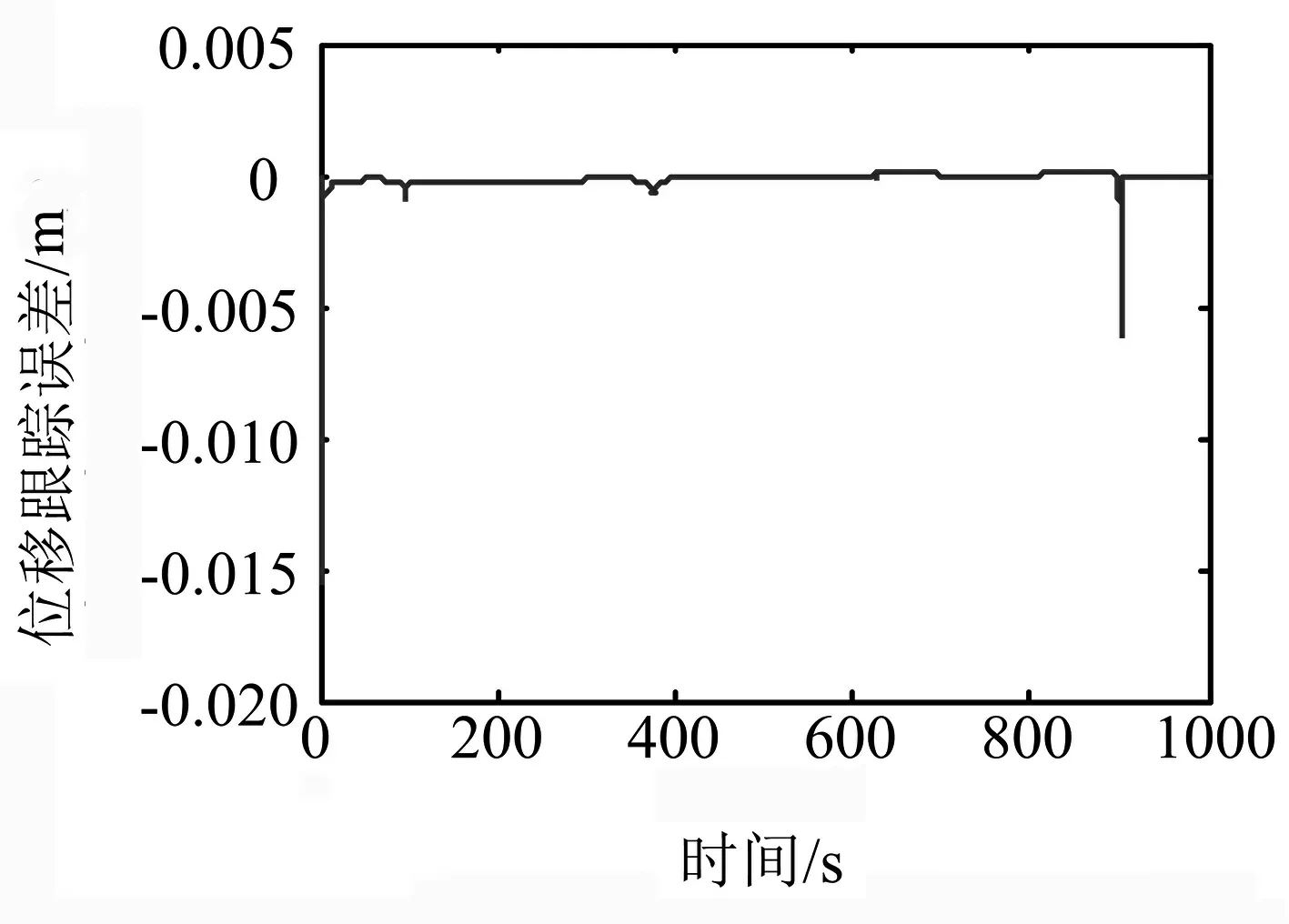
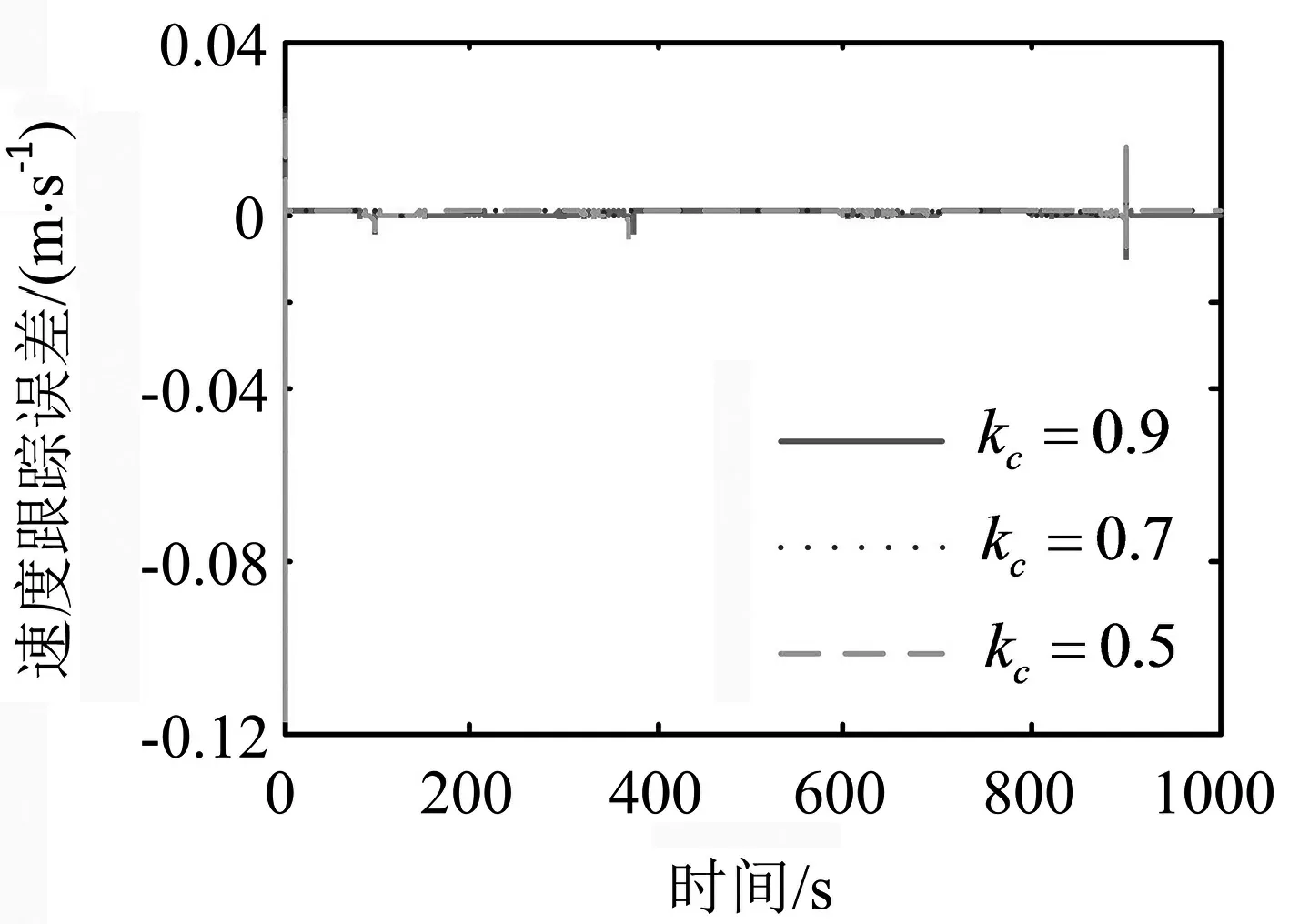
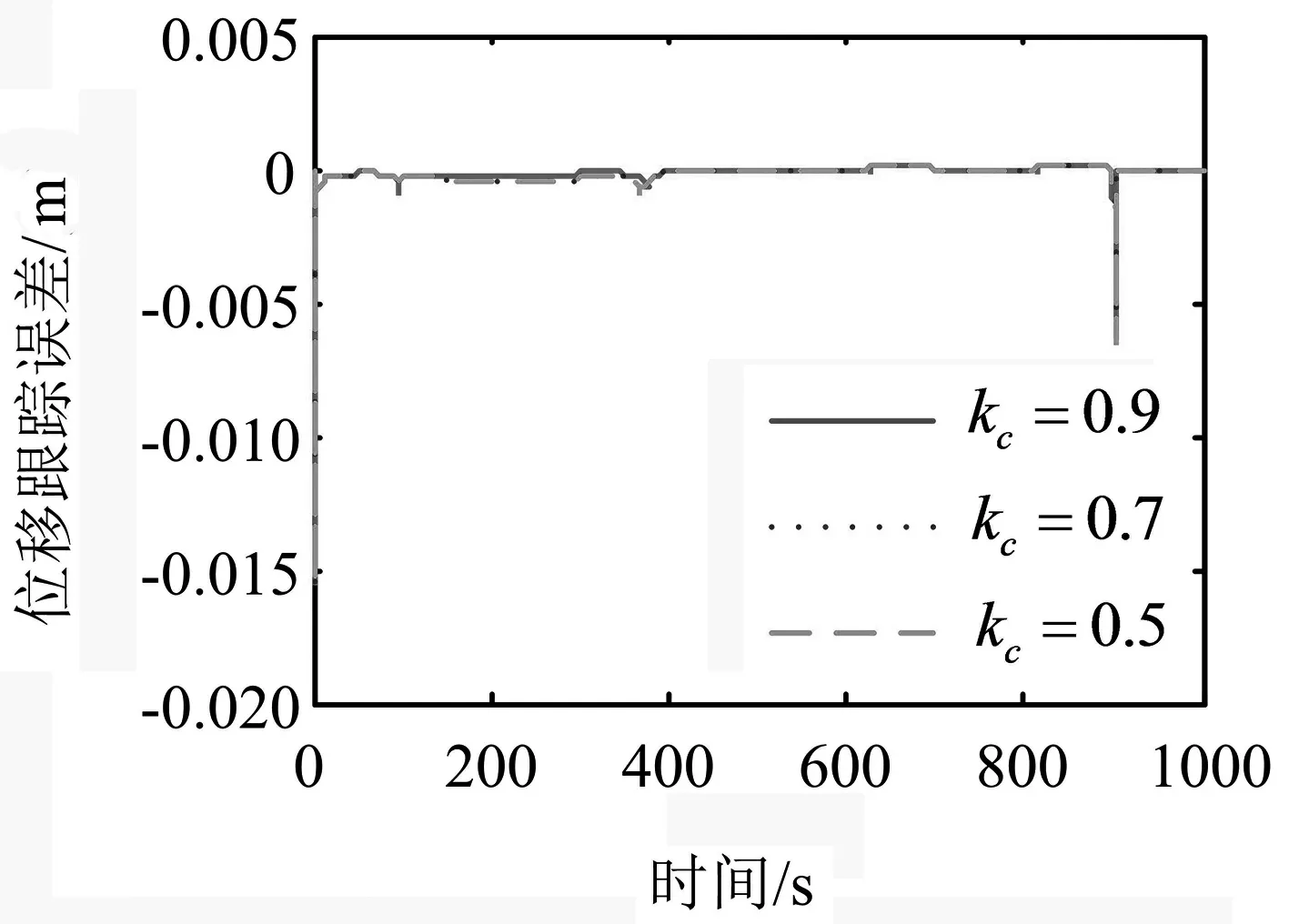
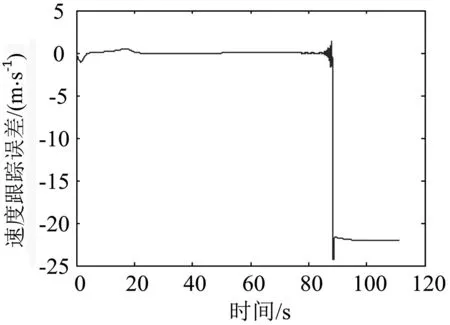
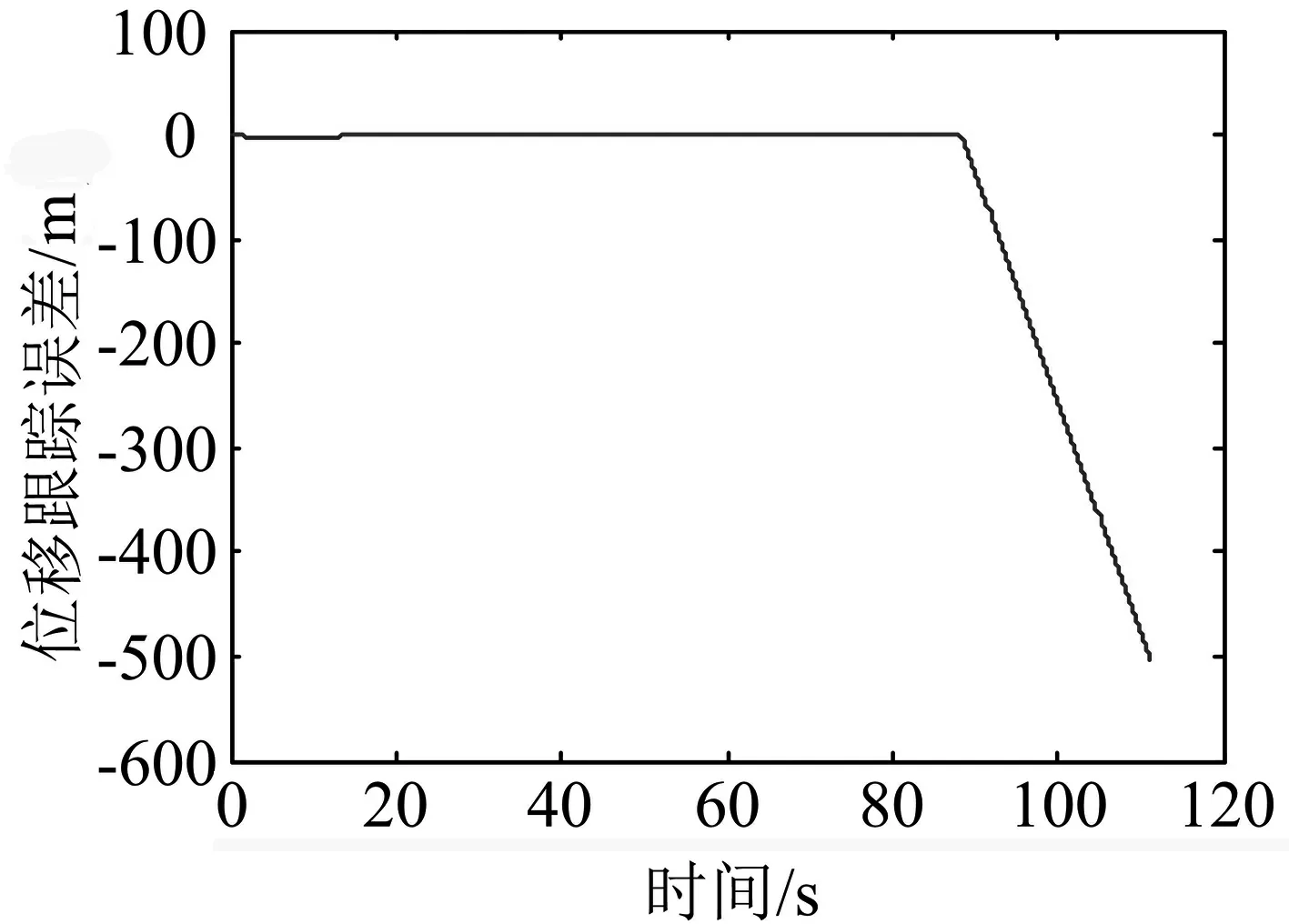
式中:F′為執行器的實際輸出;F為不考慮執行器故障時的控制器輸出;0≤kc≤1表示執行器效率,其中,kc=0表示執行器完全失效;kc=1表示執行器完全健康;0 考慮執行器效率部分損失故障,式(1)可寫為 (4) 為了方便分析以及后文容錯跟蹤控制器的設計,定義kc=1-τc,則式(4)進一步變為 (5) 假設1假設0≤τc<δ<1,其中δ未知. 備注1:假設1表示即使執行器發生故障,它仍然有能力提供必要的驅動列車跟蹤目標優化曲線的牽引力/制動力.當執行機構故障變得很嚴重,其所產生的最大牽引力/制動力不足以完成列車跟蹤任務時,必須采取比如修正目標曲線等其他措施. 控制器的控制目標是:針對式(5)構成的系統,考慮列車模型參數不確定性和執行器效率部分損失故障,設計列車容錯跟蹤控制器,使得閉環系統穩定,列車能夠精確跟蹤目標速度和位移曲線. (6) 其中,β為任意選擇的正實數.求s對時間的一階導數,可得 (7) 結合式(5),可得到 (8) 基于自適應控制技術,本文設計的高速列車容錯跟蹤控制器形式如下: F=F0+F1+F2 (9) (10) (11) F2=-ks (12) 其中,k>0為控制器參數;sign(s)為符號函數. 設計未參數的自適應更新律分別為 (13) (14) (15) (16) (17) 對于本文設計的高速列車容錯跟蹤控制器,其主要結果總結為定理1. 定理1對于式(5)所描述的模型參數不確定且存在執行器效率部分損失故障的高速列車動力學模型,設計式(9)~(12)所示的容錯跟蹤控制器及式(13)~(17)所示的參數自適應更新律,則高速列車的速度跟蹤誤差和位移跟蹤誤差將漸進收斂到零. 證明:定義估計誤差: (18) 選擇Lyapunov函數 (19) 求V對時間的一階導數 (20) 將式(8)和(9)代入式(20),可得 (21) 為了方便證明,將式(21)寫為 (22) 其中,Φ1、Φ2和Φ3的表達式分別為 (23) (24) Φ3=s(1-τc)F2 (25) 將式(10)、(13)~(16)代入式(23),可以得到 (26) 結合式(11)、(17)及式(24),可得到Φ2滿足如下關系 (27) 將式(12)代入式(25),可知 Φ3=-k(1-τc)s2≤-k(1-δ)s2 (28) 由式(26)~(28),式(22)變為 (29) 成立.此外,很明顯閉環列車跟蹤控制系統可以保證漸進穩定性,從而控制目標實現.證明完畢. 不考慮執行器故障時的高速列車自適應跟蹤控制器由式(9)、(10)和(12)構成,未知參數自適應更新律見式(13)~(16).證明過程參照上文可以很容易得到,本文省略. 備注2:本文所提出的控制算法不依賴于模型參數的先驗知識,不需要執行器故障信息,不需要故障檢測和診斷設備.盡管引入了參數δ,但是它僅出現在證明過程,控制律和自適應更新律中均不需要δ. 為了驗證本文所提出容錯跟蹤控制器的有效性,基于MATLAB軟件進行了仿真驗證.仿真所用列車參數為[21]:M=500 ton,g=9.8 N/kg,a0=5 880 N,a1=388 N·s·m-1,a2=8 N·s2·m-2. 控制器以及自適應更新律參數取值為:k=100,l0=10,l1=10,l2=10,lm=20 000,b=1000,仿真中涉及的參數初始值分別為: 為了減小抖振,使控制力平滑,本文采用邊界層方法,當|s|≤ε,用s/ε代替sign(s),其中ε為一個很小的正常數. 為了驗證所設計容錯跟蹤控制器的跟蹤性能,仿真模擬了列車在1 000 s內的運行過程.整個過程運行距離為47.5 km,最高運行時速為69.5 m/s(約250 km/h),包含兩個加速階段,四個巡航階段,兩個減速階段,所對應的目標速度和位移曲線如圖2所示. (a) 目標速度曲線 (b) 目標位移曲線圖2 目標速度和位移曲線 為了驗證所提出控制器的可行性,首先對執行器未發生故障情況進行了仿真,列車的速度跟蹤誤差和位移跟蹤誤差如圖3所示.可以看出,所提出的控制器實現了對目標速度和位移軌跡的精確跟蹤.圖3說明本文所提出的高速列車跟蹤控制器是可行有效的. (a) 速度跟蹤誤差 (b) 位移跟蹤誤差圖3 執行器未發生故障時的跟蹤誤差 為了驗證所提出控制器的容錯跟蹤能力,對執行器不同程度效率損失故障下的列車跟蹤控制系統進行了仿真.通過改變執行器有效系數kc的數值,來模擬不同程度的執行器故障.假設執行器故障發生在150 s,并持續到仿真結束.仿真中考慮了執行器效率損失分別為10%、30%和50%(分別對應kc=0.9、kc=0.7和kc=0.5)三種情況.列車的速度跟蹤誤差和位移跟蹤誤差如圖4所示. kc減小,意味著執行器效率降低,執行器故障程度越來越嚴重,故障對列車跟蹤運行的影響也越來越大.但是,從圖4可以看出,速度跟蹤誤差和位移跟蹤誤差并沒有隨著執行器故障程度的嚴重顯著增加,而是始終保持較小數值.圖4表明, 所提出的控制器能夠補償執行器效率損失故障,具有良好的容錯跟蹤能力. (a) 速度跟蹤誤差 (b) 位移跟蹤誤差圖4 執行器不同程度故障下的跟蹤誤差 為了說明考慮執行器故障設計跟蹤控制器的必要性和有效性,對實際執行器存在故障,但跟蹤控制器設計過程并未考慮執行器故障的情況進行了仿真.當執行器效率損失為30%(即kc=0.7)時,高速列車的速度跟蹤誤差和位移跟蹤誤差如圖5所示. (a) 速度跟蹤誤差 (b) 位移跟蹤誤差圖5 不考慮執行器故障設計跟蹤控制器的跟蹤誤差 可以看出,未考慮執行器故障設計的跟蹤控制器,在存在執行器故障時,系統的速度跟蹤誤差和位移跟蹤誤差大幅增加,系統跟蹤效果變得很差.對比圖5和圖4中kc=0.7時的仿真結果可以看出,考慮執行器故障設計跟蹤控制器是必要的,本文所設計的容錯跟蹤控制策略是有效的. 本文針對高速列車自動駕駛中的速度和位移跟蹤控制問題,建立了存在模型參數不確定性和執行器效率部分損失故障的列車動力學模型,設計了列車的自適應被動容錯跟蹤控制器,并進行了嚴格的理論證明和仿真驗證.所設計的容錯跟蹤控制器不僅實現了列車執行器故障下的精確跟蹤控制,而且不需要模型參數的先驗知識,不需要故障檢測與診斷模塊,使得列車在運行中,在模型參數不斷變化以及發生執行器效率損失故障的情況下,不必重新設計列車跟蹤控制器.基于Lyapunov穩定性理論證明了列車的速度跟蹤誤差和位移跟蹤誤差可以收斂到零.仿真結果顯示了該控制器的可行性、應對執行器效率部分損失故障的有效性,以及良好的容錯跟蹤能力.本文以單質點列車動力學模型為研究對象,對執行器故障的設定較為簡單.針對多質點列車動力學模型,更加合理地對執行器故障進行描述和設定,設計高速列車的容錯跟蹤控制器是接下來的研究方向.2 控制器設計及穩定性分析
2.1 控制器設計
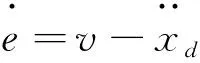
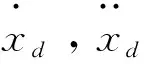
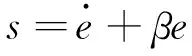
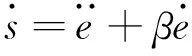
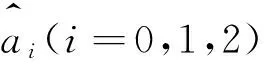
2.2 穩定性分析
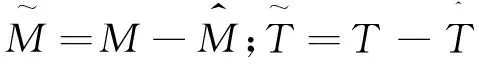
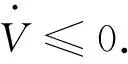
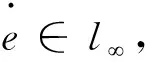

3 仿真驗證及分析
4 結論

