基于模糊雙線性模型的連續(xù)攪拌反應(yīng)釜滑模控制

陳 珺,陳 漢

(江南大學(xué) 輕工過程與先進(jìn)控制教育部重點(diǎn)實(shí)驗(yàn)室，江蘇 無錫 214122)

0 引言

滑模控制是一種變結(jié)構(gòu)控制，在非線性系統(tǒng)的分析中得到廣泛應(yīng)用，其優(yōu)點(diǎn)顯著：響應(yīng)速度快，對于實(shí)際系統(tǒng)中存在的參數(shù)不確定性和外界的噪聲干擾具有較強(qiáng)的魯棒性，同時(shí)不需要對系統(tǒng)進(jìn)行在線辨識。因此，被廣泛應(yīng)用于機(jī)器人控制、航空航天以及化工控制等領(lǐng)域[1-3]。然而滑模控制本質(zhì)上是一類特殊的非線性控制，其非線性表現(xiàn)為控制的不連續(xù)性。由于現(xiàn)實(shí)中物理能量不可能無限大，這也限制了系統(tǒng)的加速度為有界值；此外，慣性存在于每一個(gè)系統(tǒng)中，這也導(dǎo)致滑模控制的切換量必然存在一定的滯后，正因如此，滑模控制的作用往往伴隨幅值較大的抖振。系統(tǒng)性能受這種抖振的影響很大，如果沒有妥善處理，整個(gè)系統(tǒng)的穩(wěn)定性也難以保障，且在實(shí)際系統(tǒng)中控制器也難以實(shí)現(xiàn)。若要將滑模控制應(yīng)用于非線性系統(tǒng)，可將與模糊逼近相結(jié)合，并采用基于模糊規(guī)則的模糊滑模控制方法，即可通過模糊化切換增益有效地抑制干擾項(xiàng)，并且消除抖振[4-6]。

雙線性系統(tǒng)不同于一般的線性系統(tǒng)，有其特殊性，主要有兩點(diǎn)表現(xiàn)：第一，它僅比線性系統(tǒng)多了狀態(tài)變量和輸出變量的乘積，即雙線性項(xiàng)，形式上接近于線性系統(tǒng)，這種形式結(jié)構(gòu)簡易，因此便于控制；第二，對于一些特殊的非線性系統(tǒng)，其擁有比傳統(tǒng)線性系統(tǒng)高得多的準(zhǔn)確描述對象的能力。因此自問世之初，就引起了廣泛關(guān)注并在許多領(lǐng)域得到了應(yīng)用：核工程，信號和圖像處理，通信，生物，生化，社會經(jīng)濟(jì)等[7-10]。近幾十年來，許多學(xué)者研究了這類特殊系統(tǒng)的控制器設(shè)計(jì)和穩(wěn)定性分析[11-13]。

T-S模糊模型可以以任意精度有效逼近實(shí)際被控對象，擁有良好的描述非線性系統(tǒng)的能力。鑒于雙線性系統(tǒng)的特殊性，將T-S模糊模型和雙線性系統(tǒng)相結(jié)合，模糊雙線性模型應(yīng)運(yùn)而生。因其具有更好的描述非線性系統(tǒng)的能力，對T-S模糊雙線性系統(tǒng)的研究引起了學(xué)者的廣泛關(guān)注[14-16]。文獻(xiàn)[14]研究了一類具有不確定性的連續(xù)模糊雙線性系統(tǒng)容錯(cuò)控制問題，并結(jié)合了輸出反饋和觀測器以提升系統(tǒng)在故障狀態(tài)的穩(wěn)定性，文獻(xiàn)[15]則討論了不確定雙線性混沌系統(tǒng)的魯棒自適應(yīng)同步問題，文獻(xiàn)[16]對一類具有擾動(dòng)的仿射雙線性系統(tǒng)設(shè)計(jì)了魯棒H∞模糊輸出反饋控制器。

然而，在這些成果中，控制器的設(shè)計(jì)都是基于狀態(tài)反饋或者輸出反饋，形式較為單一，并且控制器的結(jié)構(gòu)較為復(fù)雜，導(dǎo)致了較大的計(jì)算量。因此，一些學(xué)者研究了基于模糊雙線性系統(tǒng)的滑模控制[17-18]。文獻(xiàn)[17]考慮了帶有模糊雙線性噪聲的滑模控制。文獻(xiàn)[18]提出了一種將滑模控制應(yīng)用于齊次雙線性系統(tǒng)的控制方法，然而若將其應(yīng)用于非齊次雙線性系統(tǒng)，在有擾動(dòng)情況下存在靜差，精度難以保證。

基于上述原因，本文主要研究了一種可以應(yīng)用于非齊次模糊雙線性系統(tǒng)的模糊滑模控制方法。首先，根據(jù)系統(tǒng)結(jié)構(gòu)構(gòu)造積分滑模面，從而保證控制精度。當(dāng)系統(tǒng)處于滑模面，為維持系統(tǒng)處于滑模面從而保證系統(tǒng)穩(wěn)定性并滿足性能指標(biāo)，推導(dǎo)等效控制量。當(dāng)系統(tǒng)狀態(tài)游離于滑模面之外時(shí)，根據(jù)構(gòu)造好的滑模面和趨近律，設(shè)計(jì)切換控制量，這樣即可保證滑模控制的可達(dá)性。接著，根據(jù)滑模面和滑模面導(dǎo)數(shù)的范圍對切換控制量進(jìn)行模糊化處理，使控制量平滑化，便于實(shí)現(xiàn)。最后，以基于模糊雙線性系統(tǒng)的連續(xù)攪拌反應(yīng)釜的仿真實(shí)例驗(yàn)證了所提方法的有效性。

1 問題描述

考慮一類由T-S模糊雙線性模型描述的非線性系統(tǒng)，其第i條規(guī)則如下：

Plant Rule i: IF ?1(t) isMi1and … and ?p(t) isMip,

THEN

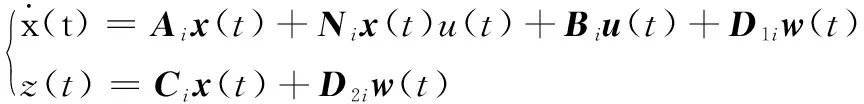
(1)

其中:x(t)∈Rn為狀態(tài)向量，u(t)∈Rm為控制輸入，w(t)∈Rl為平方可積的干擾輸入向量，且滿足|w(t)|≤d；?1(t),...?p(t)為模糊規(guī)則的前件變量，Mij(j=1,2,...,p)為模糊集合，r為模糊規(guī)則推理數(shù)。Ai,Ni,Bi,D1i,Ci,D2i為具有適當(dāng)維數(shù)的已知常數(shù)矩陣。

采用單點(diǎn)模糊化、乘積推理以及加權(quán)平均反模糊化的方法，可得模糊雙線性系統(tǒng)的整體方程為:

(2)

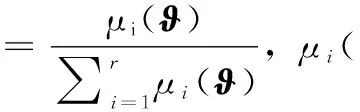
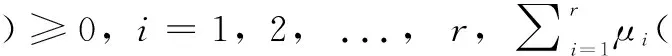
2 滑模控制器設(shè)計(jì)與穩(wěn)定性證明

滑模控制方法可將系統(tǒng)狀態(tài)引導(dǎo)到事先定義好的滑模面，并使其滑向平衡點(diǎn)。因此，滑模控制通常有切換控制us和等效控制ueq兩個(gè)部分組成。切換控制是不連續(xù)的，并且只當(dāng)系統(tǒng)不在滑模面時(shí)起作用，等效控制是連續(xù)的，目的是使系統(tǒng)在滑模面上運(yùn)行。滑模控制器形式為:

u=us+ueq

(3)

接下來推導(dǎo)兩個(gè)控制分量的具體結(jié)構(gòu)與穩(wěn)定性證明。

2.1 等效控制量

首先，定義如下積分滑模面:

(4)

傳統(tǒng)滑模面為線性滑模面，即只有上式前一項(xiàng)，形式如下：

S(x)=Cx=0

該類滑模控制系統(tǒng)穩(wěn)定性分析簡單、便捷，參數(shù)設(shè)計(jì)相對容易，故線性滑模最早被提出，并應(yīng)用廣泛。但線性滑模在復(fù)雜非線性系統(tǒng)中應(yīng)用的控制效果略顯不足：對于帶有擾動(dòng)的復(fù)雜系統(tǒng)，會出現(xiàn)狀態(tài)分量之間的誤差成比例存在，此時(shí)滑模面函數(shù)也為0，這就造成控制精度難以保證。為此，采用式(4)的積分滑模面，積分項(xiàng)的引入，可顯著提高控制精度。

為保證系統(tǒng)可以處于滑模面上運(yùn)行，從而達(dá)到平衡點(diǎn)，需滿足以下條件：當(dāng)滑模面已經(jīng)到達(dá)時(shí)，即S=0時(shí)，有：

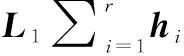
(5)

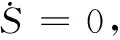
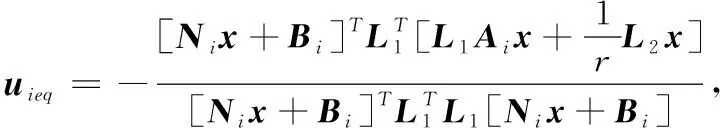
L1[Nix+Bi]≠0

(6)

結(jié)合并行分布補(bǔ)償(PDC)算法，整體的等效控制量為:

(7)

為保證系統(tǒng)可在控制量(7)的作用下于滑模面上漸近穩(wěn)定，給出如下定理：

定理1：若存在一個(gè)對稱正定矩陣P，和L1，L2滿足如下線性矩陣不等式(8)，則模糊雙線性系統(tǒng)(2)在等效控制器(7)的作用下是漸近穩(wěn)定的。

(8)

證明：取Lyapunov函數(shù)為V1=xTPx，P為正定對稱矩陣。對V1的時(shí)間t進(jìn)行求導(dǎo)得:

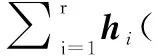
將等效控制量式(6)代入得:

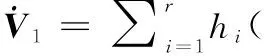
若滿足如下條件:

(9)

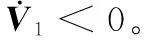
證畢。

2.2 切換控制量

滑模面設(shè)計(jì)可以保證滑動(dòng)模態(tài)運(yùn)動(dòng)品質(zhì)，滑模切換控制律則可以保證系統(tǒng)有限時(shí)間可達(dá)性和提高趨近階段的動(dòng)態(tài)品質(zhì)，使系統(tǒng)進(jìn)入滑動(dòng)模態(tài)。可達(dá)性指系統(tǒng)狀態(tài)在有限時(shí)間內(nèi)到達(dá)滑模面。滑模切換控制律可以根據(jù)趨近律設(shè)計(jì)，常見的趨近律有等速趨近律，指數(shù)趨近律，冪次趨近律，這里滑模切換控制器的設(shè)計(jì)是基于等速趨近律。

當(dāng)滿足如下條件，則滑模面的可達(dá)性可以保證：

(10)

為此，設(shè)計(jì)切換控制器形式為:

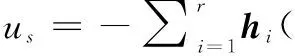
K≥L1D1id,L1(Nix+Bi)≠0

(11)

定理2：在控制器(7)和(11)的共同作用下，且滿足L1[Nix(t)+Bi]≠0時(shí)，系統(tǒng)(2)將滿足可達(dá)性。

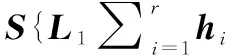
(12)

將式(3)代入式(12)中得：

D1iw]+L2x}=

證畢。

滑模控制的魯棒性由切換控制得到保證，然而滑模控制的抖振也由切換控制中的符號項(xiàng)造成：當(dāng)系統(tǒng)狀態(tài)到達(dá)滑模面，由于慣性的影響，系統(tǒng)狀態(tài)將穿過滑模面，此時(shí)在符號項(xiàng)的作用下，切換控制量符號瞬間取反，而增益不變，控制器輸出變化劇烈，相應(yīng)地，系統(tǒng)狀態(tài)也會受其影響；當(dāng)系統(tǒng)狀態(tài)變化趨勢已經(jīng)處于滑模面附近時(shí)，狀態(tài)量就會在控制器的作用下頻繁穿越滑模面，這就是系統(tǒng)抖振。

為了消除抖振，應(yīng)使切換控制在保證魯棒性的同時(shí)盡量小，常用的方法有模糊推理，自適應(yīng)滑模控制，高階滑模等，這里使用的是曼達(dá)尼模糊推理。

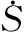
此時(shí)切換控制量形式為：

K≥L1D1id,L1(Nix+Bi)≠0

(13)

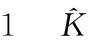
表模糊規(guī)則表

3 應(yīng)用實(shí)例

連續(xù)攪拌反應(yīng)釜(CSTR)是工業(yè)過程中最常用的一種化學(xué)反應(yīng)器，它可以實(shí)現(xiàn)聚合反應(yīng)，在石油、醫(yī)藥、試劑、食品以及合成材料等工業(yè)生產(chǎn)過程中占有相當(dāng)重要的地位。一般來說，CSTR是在與最佳生產(chǎn)率相聯(lián)系的某個(gè)平衡點(diǎn)上運(yùn)行的，以追求最大的經(jīng)濟(jì)效益。從控制的角度來說，CSTR具有高度的非線性，特別是在具有外部干擾的情況下，因此難以通過常規(guī)方法取得令人滿意的效果。為了驗(yàn)證所提方法的控制效果，以下將以CSTR系統(tǒng)為對象進(jìn)行仿真研究。CSTR狀態(tài)方程(14)如下[19]：

(14)

其中：x1(t)為反應(yīng)釜中反應(yīng)物的濃度，x2(t)為生成物的濃度，控制輸入u(t)為稀釋比例，w(t)=e-tsin(5t)為擾動(dòng)。系統(tǒng)中動(dòng)力參數(shù)選為k1=50 h-1，k2=100 h-1，k3=10 L/mol·h，CA0=10 mol/L。

假設(shè)x1(t)∈[0,10]，采用兩個(gè)T-S模糊雙線性模型來逼近CSTR系統(tǒng)(14)，即:

Rule 1: Ifx1(t) is about 0, THEN:

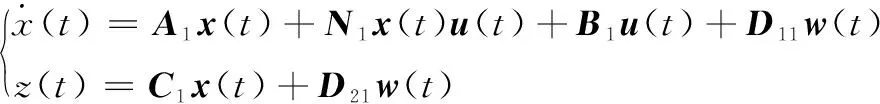
Rule 2: Ifx1(t) is about 10, THEN：

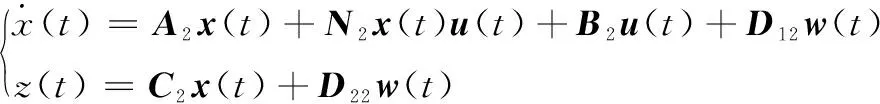
其中系統(tǒng)參數(shù)矩陣如下：

對應(yīng)規(guī)則的模糊隸屬度函數(shù)為：

h1(x1(t))=1-0.1x1(t)，h2(x1(t))=0.1x1(t)。

為便于比較，取系統(tǒng)(14)的一個(gè)平衡點(diǎn)：

xd(t)=[4.5 1.266]T，ud(t)=77.7272。

此時(shí)先將系統(tǒng)轉(zhuǎn)化為基于誤差的系統(tǒng)，形式如下：

Ni(e(t)+xd)u(t)+Biu(t)+D1iw(t)]

(15)

其中：e(t)=x(t)-xd(t)。

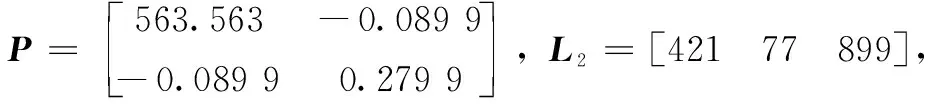
(16)

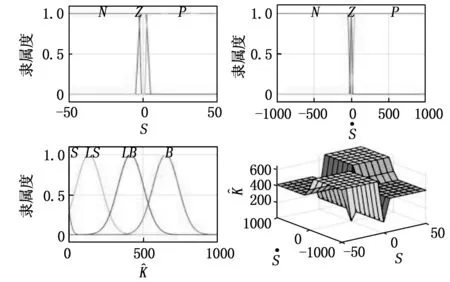
圖的模糊規(guī)則隸屬度函數(shù)

圖2給出了該系統(tǒng)在初始條件x0(t)=[5.5 -1.8]T下的狀態(tài)響應(yīng)。由仿真結(jié)果可以看出，初始狀態(tài)與平衡點(diǎn)差距較大，且伴有擾動(dòng)。但在控制器(3)的作用下，系統(tǒng)狀態(tài)響應(yīng)經(jīng)過短暫的過渡過程(大約0.1 s)后即可維持在給定的平衡點(diǎn)xd(t)=[4.5 1.266]T附近，因此所設(shè)計(jì)的控制器可以保證模糊雙線性系統(tǒng)是漸近穩(wěn)定的。

圖3則是文獻(xiàn)[18]的方法應(yīng)用于連續(xù)攪拌反應(yīng)釜的效果。對比文獻(xiàn)[18]可知，文獻(xiàn)[18]沒有考慮擾動(dòng)對系統(tǒng)的影響，且采用的滑模面為傳統(tǒng)的線性滑模面。因此在有擾動(dòng)的情況下，系統(tǒng)雖能維持穩(wěn)定，但系統(tǒng)的狀態(tài)和平衡點(diǎn)之間存在靜差，且狀態(tài)與控制量均持續(xù)抖動(dòng)難以穩(wěn)定；另外，由于切換增益無法隨擾動(dòng)改變，系統(tǒng)狀態(tài)受擾動(dòng)影響變化幅值明顯大于本文所提方法。而本文在干擾存在的情況下仍能取得較快的響應(yīng)時(shí)間和較好的過渡過程特性，并且控制精度也得到了保障。

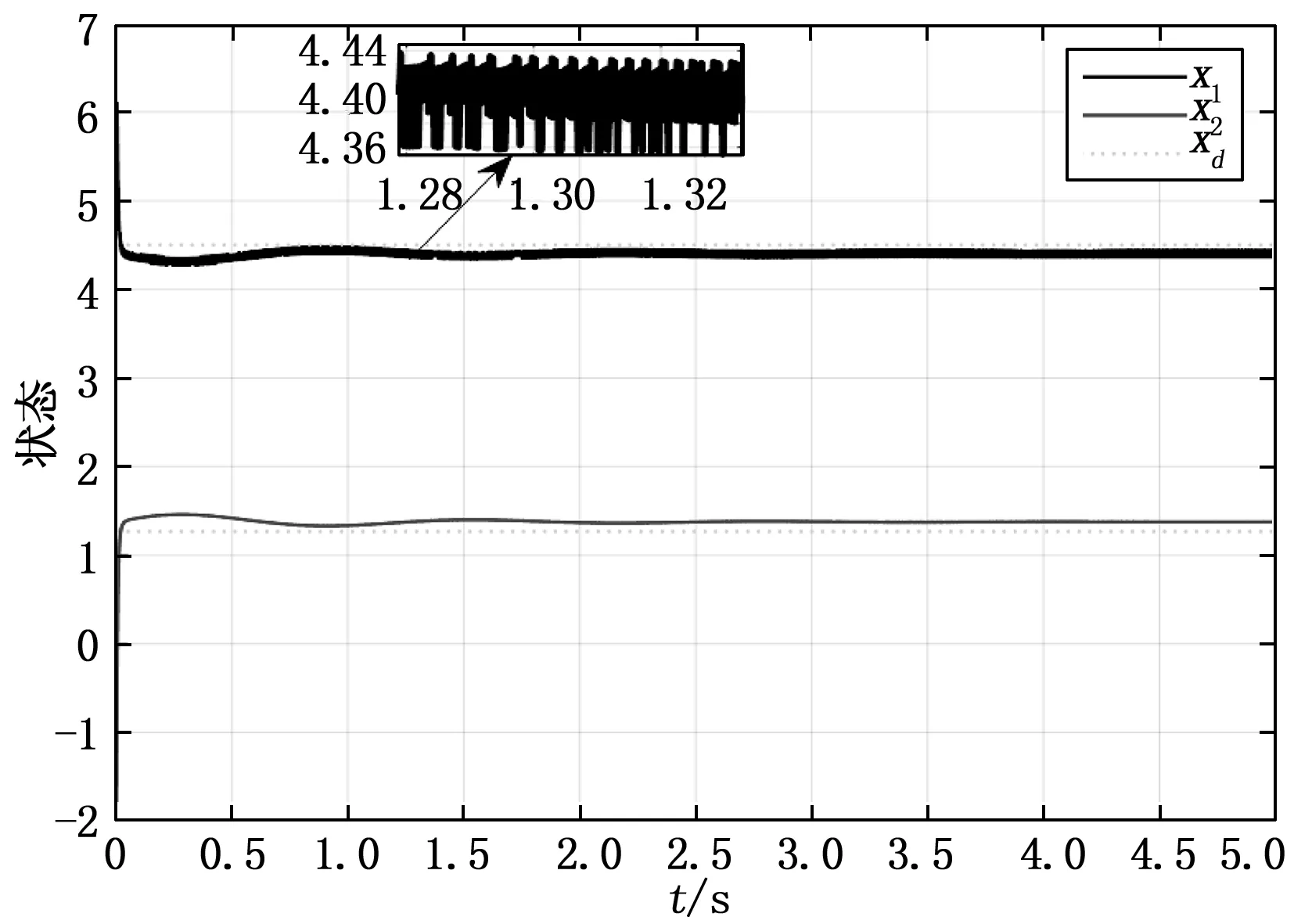
圖3 文獻(xiàn)[18]狀態(tài)響應(yīng)曲線

圖4是本文提出的與狀態(tài)響應(yīng)相應(yīng)的控制曲線。由圖可知，控制量由大約58迅速升至平衡點(diǎn)77.727 2附近，為了克服擾動(dòng)，存在一定的抖振，但在7條模糊規(guī)則的作用下，控制量逐漸平滑，實(shí)現(xiàn)了實(shí)際中的可操作性。當(dāng)擾動(dòng)消失時(shí)，控制量也穩(wěn)定在平衡點(diǎn)。

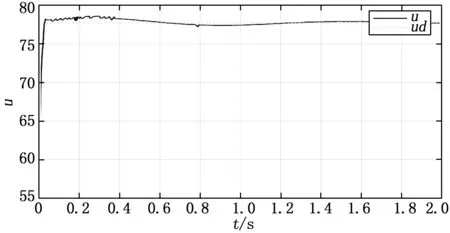
圖4 系統(tǒng)的控制曲線

圖5為滑模面函數(shù)對時(shí)間變化的曲線。由圖可知滑模面一開始大約在42左右，這是因?yàn)槌跏紶顟B(tài)與平衡點(diǎn)之間差距較大。但在滑模控制器的作用下迅速降至0左右，緊接著由于控制器抖振引起狀態(tài)的抖振，滑模面函數(shù)也相應(yīng)地小幅度起伏，但隨即與控制量一起穩(wěn)定下來。

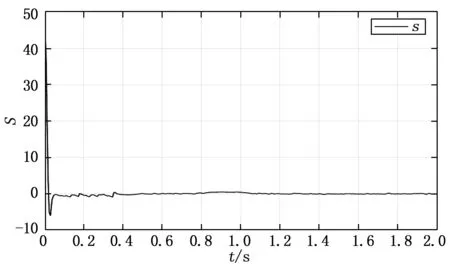
圖5 滑模面隨時(shí)間變化曲線

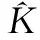
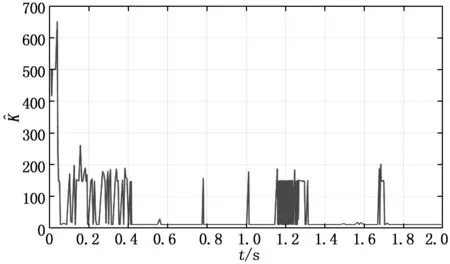
圖隨時(shí)間變化曲線

4 結(jié)束語

本文以連續(xù)CSTR為研究對象，引用T-S模糊雙線性模型對其進(jìn)行控制。通過對滑模控制中等效控制和切換控制的設(shè)計(jì)，給出了一個(gè)新的保證閉環(huán)模糊雙線性系統(tǒng)全局漸近穩(wěn)定的控制方法，從而使得系統(tǒng)具有較強(qiáng)的魯棒性。模糊規(guī)則的引入解除了滑模控制的抖振現(xiàn)象，使得控制量連續(xù)化并且具有可實(shí)現(xiàn)性。最終通過仿真研究，驗(yàn)證了本文方法的有效性。

但是，本文的控制器設(shè)計(jì)也有所不足，控制器分母有一定的條件限制，滑模面的參數(shù)如果選取不當(dāng)可能導(dǎo)致系統(tǒng)運(yùn)行中發(fā)生奇異問題，從而引發(fā)系統(tǒng)不穩(wěn)定和發(fā)散。未來，可就這一問題引入事件觸發(fā)機(jī)制[20]，規(guī)避奇異問題的發(fā)生；此外，對于滑模面的選擇，可以嘗試性能更高的滑模面類型，如終端滑模面[21]，全局滑模面等，相信可以有更好的控制效果。