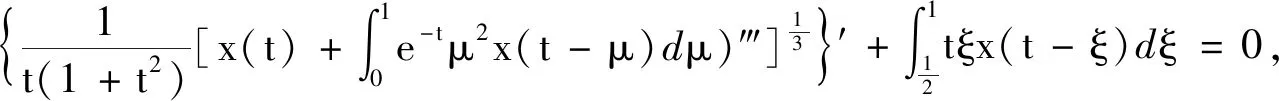一類四階中立型微分方程解的振動性
賈對紅
長治學院數學系,山西 長治 046000
0 引言
微分方程解的振動性問題被越來越多的學者所關注,本文在已有文獻[1~6]的基礎上主要研究方程
(E)
的振動性,并給出方程解的幾個振動準則.
我們做如下假設:
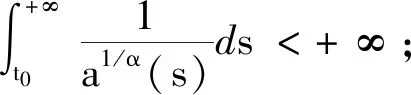
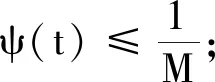
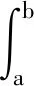
(A4)τ(t,μ)∈C([t0,+∞)×[a,b],R+),關于μ在區間[a,b]內單調遞減,且滿足τ(t,μ)≤t,
(A5)g(t,ξ)∈C([t0,+∞)×[c,d],R+),關于ξ在區間[c,d]內單調遞減,且滿足g(t,ξ)≤t,
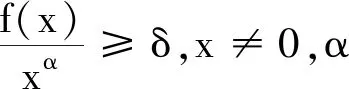
引理1 假設(A1)~(A7)成立,x(t)是方程(E)的一個最終正解,z(t)有如下情形:
(a)z(t)>0,z′(t)<0,z″(t)>0,z?(t)<0
(b)z(t)>0,z′(t)>0,z″(t)>0,z?(t)>0
(c)z(t)>0,z′(t)>0,z″(t)>0,z?(t)<0
證明 設x(t)是方程(E)的一個正解,t∈[t0,+∞),則存在充分大的t1>t0,當t>t1時,x(τ(t,μ))>0,x(g(t,ξ))>0且
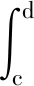
故a(t)ψ(x(t))(z?(t))α是減函數,從而有z?(t)<0或者z?(t)>0.若z?(t)<0,則z″(t)單調遞減,則z″(t)>0或者z″(t)<0.下面證明z″(t)>0,如若不然z″(t)<0,由于a(t)ψ(x(t))(z?(t))α是減函數,故存在Q>0,當t>t1時
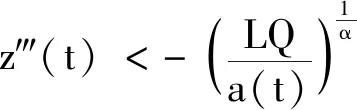
上式從[t,T]積分得
這與假設矛盾,從而知z(t)只能有上述三種情況.
引理2 若假設(A1)~(A7)成立,x(t)是方程(E)的一個最終正解,z(t)有引理 1中的情形(a),且假設
(1)
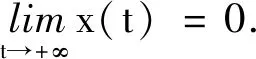
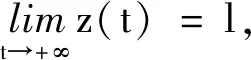
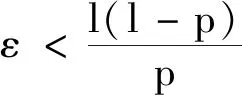
(2)
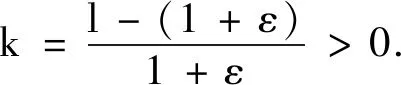
由(A6),(A7)和(2)式可得
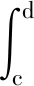
(3)
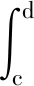
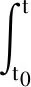
有
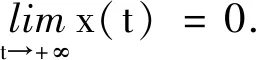
1 主要結果
設D={(t,s):t0≤s≤t<+∞};D0={(t,s):t0≤s (1)H(t,t)=0,t≥t0;H(t,s)>0,(t,s)∈D0. 定理1 假設A1~A7及條件(2)成立,若存在ρ∈C1([t0,+∞),R+)以及(t,s)∈D0滿足 (4) 其中 那么方程(E)的任何解x(t)或者是振動的或者當t趨于無窮時趨向于0. 下面分別討論情形(b),(c). 情形1 設當t>t1時,z(t)滿足情形(b),有z(t)>0,z′(t)>0,z″(t)>0,z?(t)>0,因而z(t)是單調遞增函數,則有 (5) 由假設A5,A6和A7得到 ≤-δ(1-p)αzα(g(t,d))q(t)<0 可以看出a(t)ψ(x(t))(z?(t))α是單調遞減函數,且t>s時 a(t)ψ(x(t))(z?(t))α 即 (6) 兩邊同時對s從t0到t積分,可得 (7) 兩邊同時對s從t0到t積分,可得 即有 (8) 因此對任意的t≥s≥t1時有 (9) 令 (10) 令 (11) 由(10)式有 (12) 上式兩端分別乘以H(t,s),對任意的t≥t1>t0積分得 由條件假設得 (13) 即 (14) 從而有 (15) 這與(4)矛盾. 情形2 若z(t)滿足情形(c),有z(t)>0,z′(t)>0,z″(t)>0,z?(t)<0,同情形1可以看出a(t)ψ(x(t))(z?(t))α是單調遞減函數,且t>s時 a(t)ψ(x(t))(z?(t))α 同理可得 (16) 由(5)式和(8)式得 (17) 定理2 假設A1~A7以及式(1)成立,ρ∈C1([t0,+∞),R+),φ∈C([t0,+∞),R),H∈X對任意的T≥t0,有 (18) (19) (20) φ+(s)=max{φ(s),0},則方程(E)的解或振動或趨于0. 證明 情形1 設x(t)是方程(E)的非振動解,設x(t)>0,且z(t)滿足情形(b),由條件(19),對任意的t1>t0 即對任意的t1>t0有 φ(t1)≤w(t1) 由(13)式和(18)式得 ≤w(t1)-φ(t1)<+∞ (21) 若 (22) 由條件(18)知,存在ε>0使得 (23) 對上述ε及任意的正常數N,存在t2>t1,當t>t2時有 因此對任意的t≥t2有 由N的任意性 這與式(21)矛盾,故 這與條件(20)矛盾. 情形2 若z(t)滿足情形(c)證明與情形1類似,可以得到同樣的結論.由以上證明可得方程(E)的解或振動或趨于0. 可知此方程的解或振動或趨于0.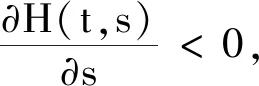
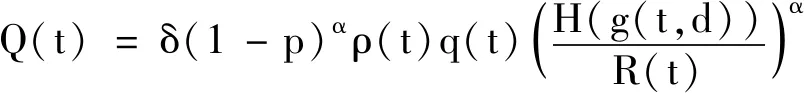
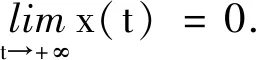
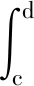
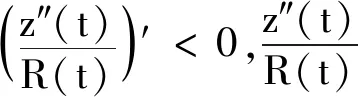
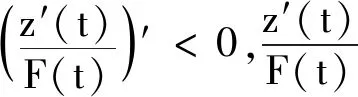
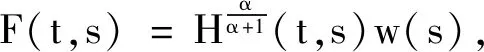
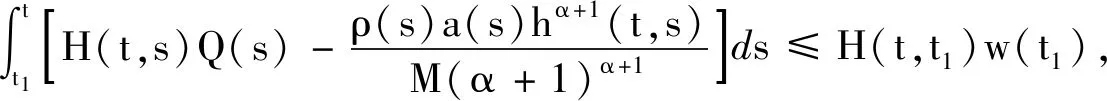
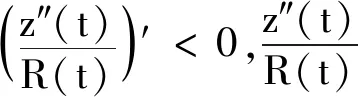
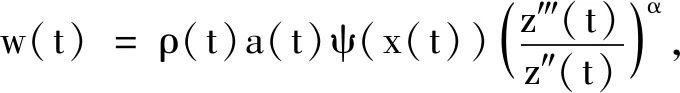
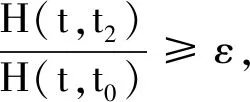
2 應用舉例