能耗與質量約束下的生產系統集成維護決策
周炳海, 易琦
(同濟大學 機械與能源工程學院, 上海 201804)
生產設備在加工過程中會發生劣化,從而導致能耗加劇、次品率上升等不良后果,造成額外的損失成本。Cai等[1]闡述了節能減排對于推動制造業綠色轉型的重要意義,質量控制在生產中占據著尤為重要的戰略位置[2]。節能、質量控制與維護決策實際上存在著權衡,因為及時的維護可以降低能耗和質量損失成本,但過多的維護將導致更多的維護成本與能耗成本[3-4],并可能引起永久生產損失。
以往的預防性維護研究將生產系統的產品質量納入考慮,Lopes[5]提出了一種針對帶有質量檢測與返工循環的生產系統的預防性維護綜合決策。Wang等[6]假設生產線中的機器達到失控狀態時,會發生質量故障從而產出次品。Yang等[7]將機會監測和定期監測2種方式結合起來衡量系統的劣化程度。上述研究雖然考慮了產出質量,但是并沒有體現出系統的次品率與劣化進程的相關性,近年來針對維護策略的研究開始關注系統中的能耗問題,Zhou等[8]考慮了生產線中的低能耗和高能耗2種狀態,并用控制圖來將機器的劣化狀態分為受控區和失控區。Yu等[9]將維護調度問題表述為在線任務分配問題,目標是減少串行生產線的總體維護成本和與能源相關成本。Huang等[10]將維護與節能整合到同一模型中并引入機會維護窗口機制。Xia等[11-12]基于節能機會窗,提出了一種面向能源的維護框架(multi-attribute model,MAM)。上述研究中大多假設能耗是恒定的,并未考慮生產系統中的能耗隨著劣化發生遞增的情況;在各類預防性維護模型中,維護決策通常以單一指標為參考,周炳海等[13]以帶緩沖的串行生產系統為研究對象,以系統劣化量達到預設的維護閾值作為維護行動的觸發條件,構建了綜合考慮設備劣化和需求隨機的最優生產周期模型;陸志強等[14]也研究了類似對象,以隱馬爾科夫退化系統的工件質量指標為決策依據,提出了設備維護的在線決策策略。此類模型沒有將其他指標納入考慮,存在一定的局限性,因此聯合優化維護模型開始受到學者們的廣泛關注,因為該類模型可以同時關注除了系統劣化情況外的其余指標,如生產率、次品率等。成國慶等[15]以批量生產周期、質量控制閾值以及預知維護參數為三維聯合決策變量,建立了有限時域內混聯系統的平均費用率模型。但是目前尚沒有研究能在聯合優化模型中同時考慮到能耗、質量以及維護決策。
基于上述研究,本文提出了一種多指標集成維護框架,該框架假設系統中的運行能耗會隨著劣化進程而發生遞增,且次品率也將根據可控與不可控狀態而發生變化,集成維護模型同時為生產系統設定能耗約束與質量約束,以最小化系統總成本為目標,獲取最優的預防性維護閾值和約束組合,實現對生產系統的中節能、質量、維護的集成優化。
1 串行生產系統集成維護問題描述
針對如圖1所示的一個由n臺設備與n-1個緩沖區組成的串行生產系統,其中第k臺設備Mk為加工速率最慢的瓶頸設備。

圖1 串行生產線Fig.1 Serial production line
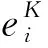
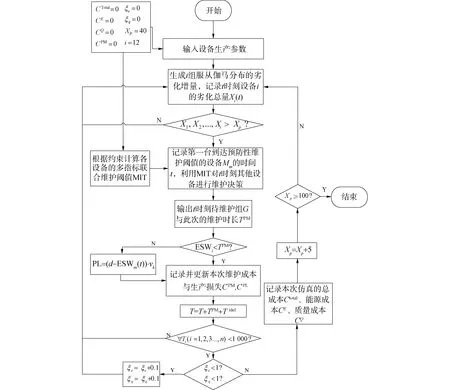
基于上述假設,首先對串行生產系統的劣化過程、設備能耗、產品質量進行建模,隨后設定能耗約束與質量約束,建立多指標集成維護閾值(multi-attribute integrated threshold,MIT)來實時監測系統內的各項指標;接著根據MIT決策出系統中的待維護設備組,并計算此次維護的節能機會窗,在時間窗內開展維護活動,以總成本最小化為目標,尋找最優的預防性維護閾值與約束組合,由此搭建多指標集成維護模型。
2 維護決策模型構建
2.1 基于伽馬過程的劣化建模
伽馬過程是一類特殊的Markov過程,具有遞增的、平穩獨立增量,適用于描述生產設備的多種劣化進程,如腐蝕、磨損、裂紋增長等。選取伽馬過程來刻畫串行生產系統上各臺設備的連續劣化過程,用Xi(t)來表示設備Mi在t時刻的劣化量。
設初始時刻設備為全新狀態,即初始劣化量Xi(t)=0,則在時刻t劣化量Xi(t)的概率密度函數為:
(1)
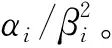
Fξ(t)=P(tξ
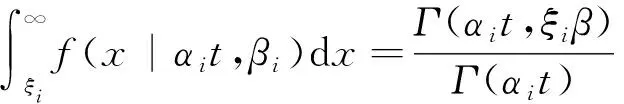
(2)
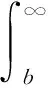
設備到達失效閾值Xf的失效時間tf的概率密度函數ftξ(t)的計算方法:
(3)
式中:ψ(a)=Γ′(a)/Γ(a)=?logΓ(a)/?a,為雙伽馬函數。
2.1.1 設備能耗
將設備Mi的運行狀態簡化為4個時間段:開機啟動、預熱、正常運行、待機,其中啟動與預熱階段的設備能耗忽略不計,正常運行階段的能耗會隨著劣化而逐漸增加,于是設備Mi的運行階段分為:
(4)
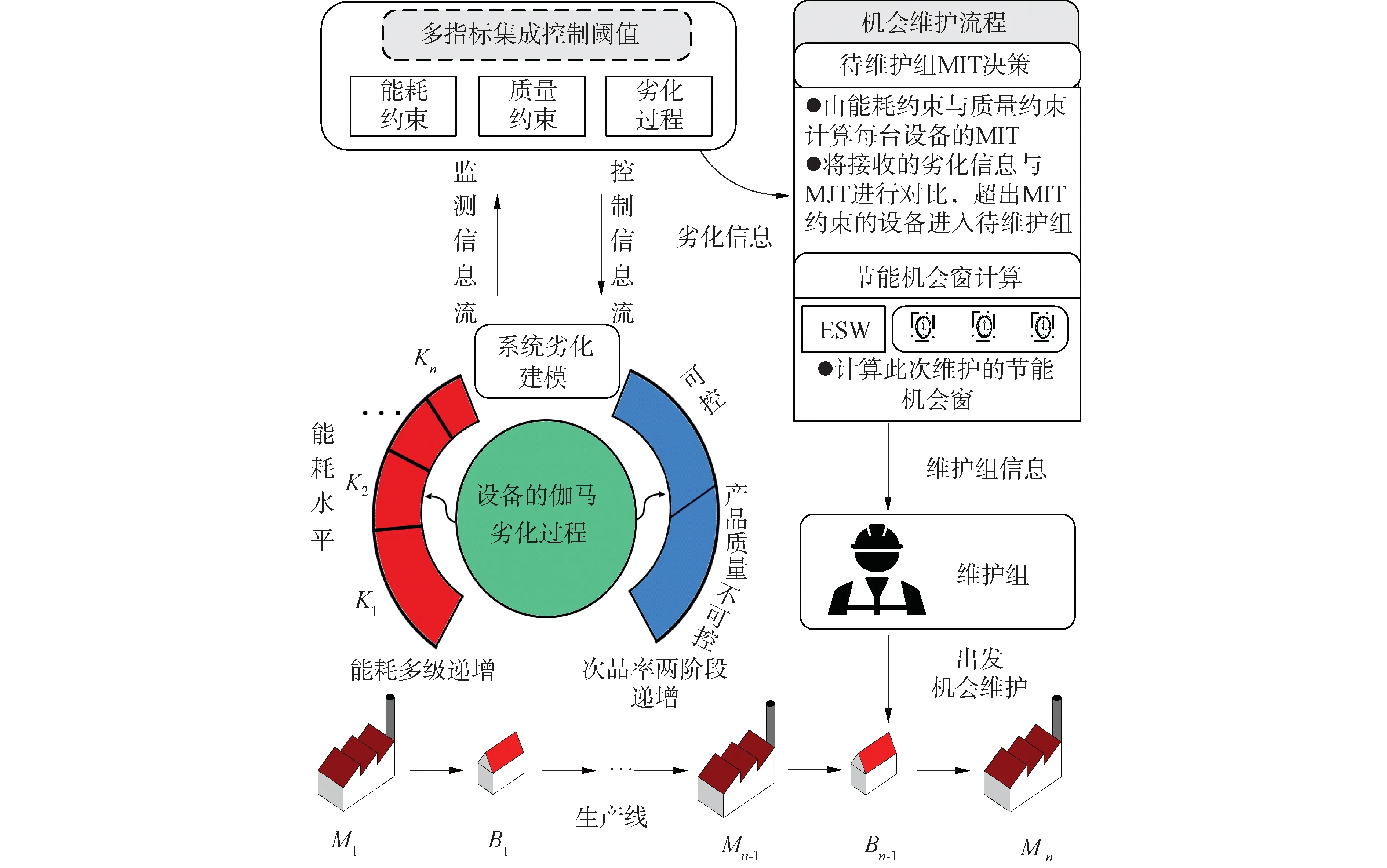
圖2 多指標集成維護框架Fig.2 Framework of multi-attribute integrated maintenance model
定義設備Mi在t時刻的劣化等級為:
(5)
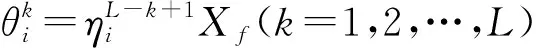
(6)
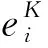
2.1.2 產品質量
隨著各設備劣化程度的加劇,其加工產品的質量性能也隨之下降,即產出次品開始增多,由Bouslah等[16]次品率是關于系統劣化量的單調遞增函數:
p(X(t))=p0+μ·[1-e(-λ·X(t)θ)]
(7)
式中:p0為系統在全新狀態下的初始次品率;μ為質量劣化的邊界值;λ、θ為正常數。
將設備劣化過程劃分為“可控”與“失控”狀態,“失控”狀態下的次品率增長速度要大于“可控”狀態,基于此概念定義狀態轉變閾值Xq,該閾值將整個次品率遞增過程離散化為可控與不可控2個狀態:
p(X(t))=
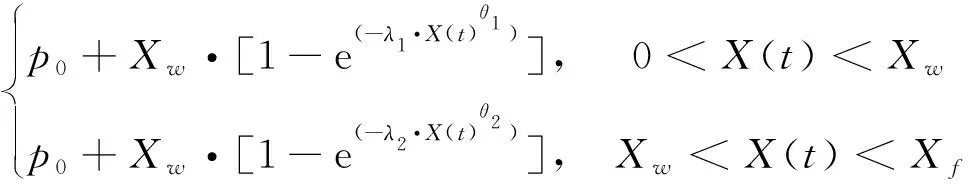
(8)
式中:參數λ1<λ2,θ1<θ2,p0為初始次品率;Xw為狀態改變閾值,當劣化量X(t)低于此閾值時產品次品率增速較慢,劣化量超出狀態改變閾值后,次品率增速明顯加快。
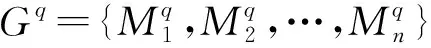
(9)
2.2 多指標集成維護閾值
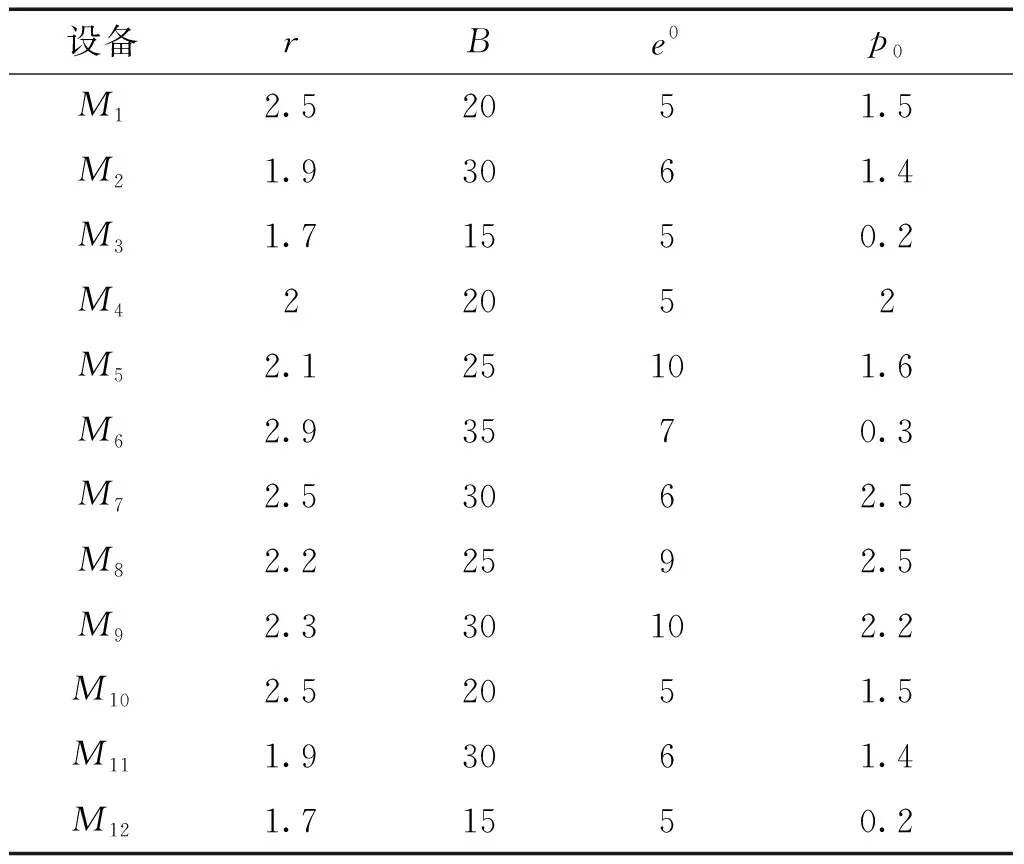
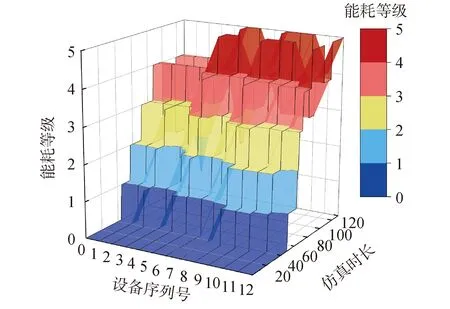
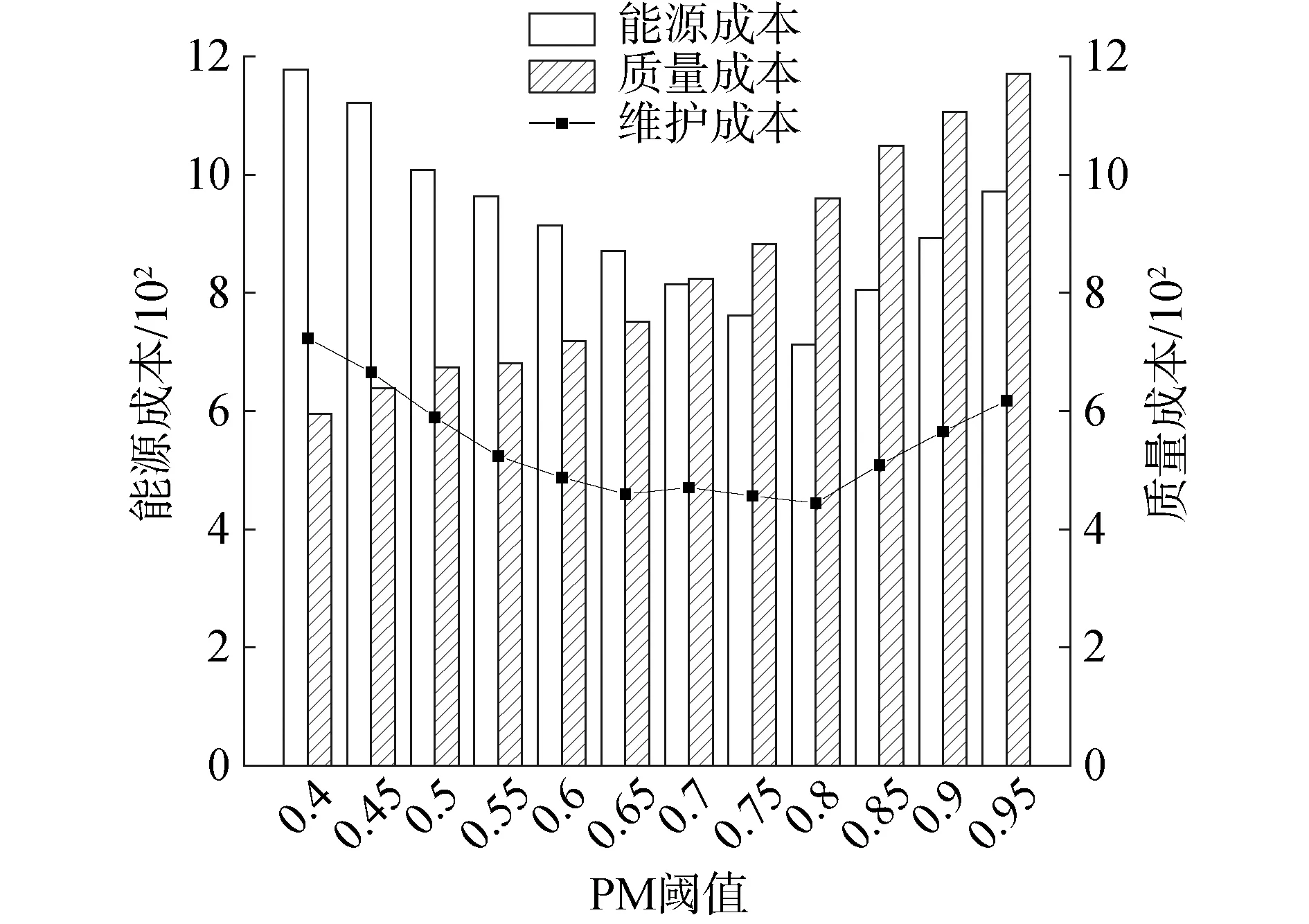
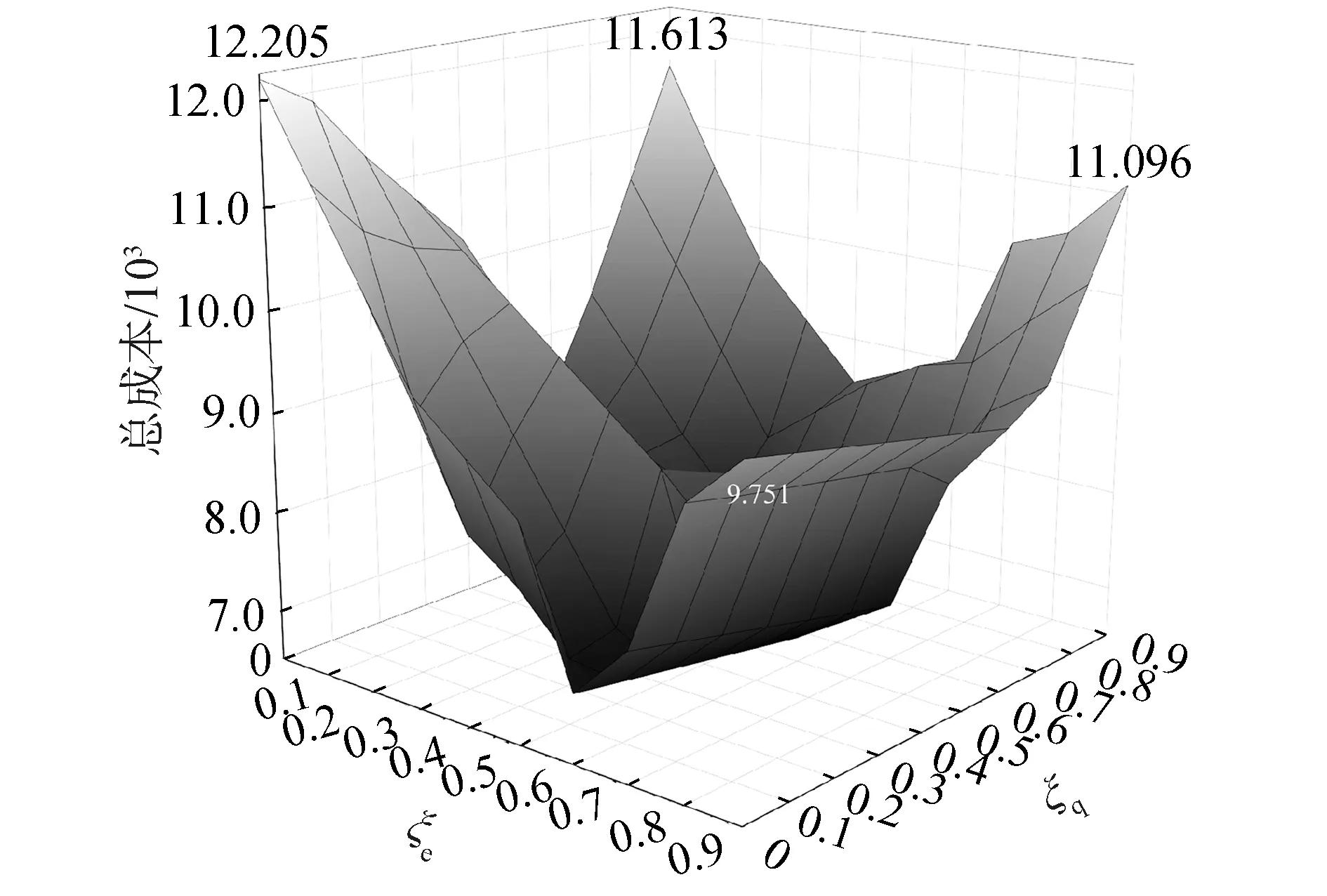
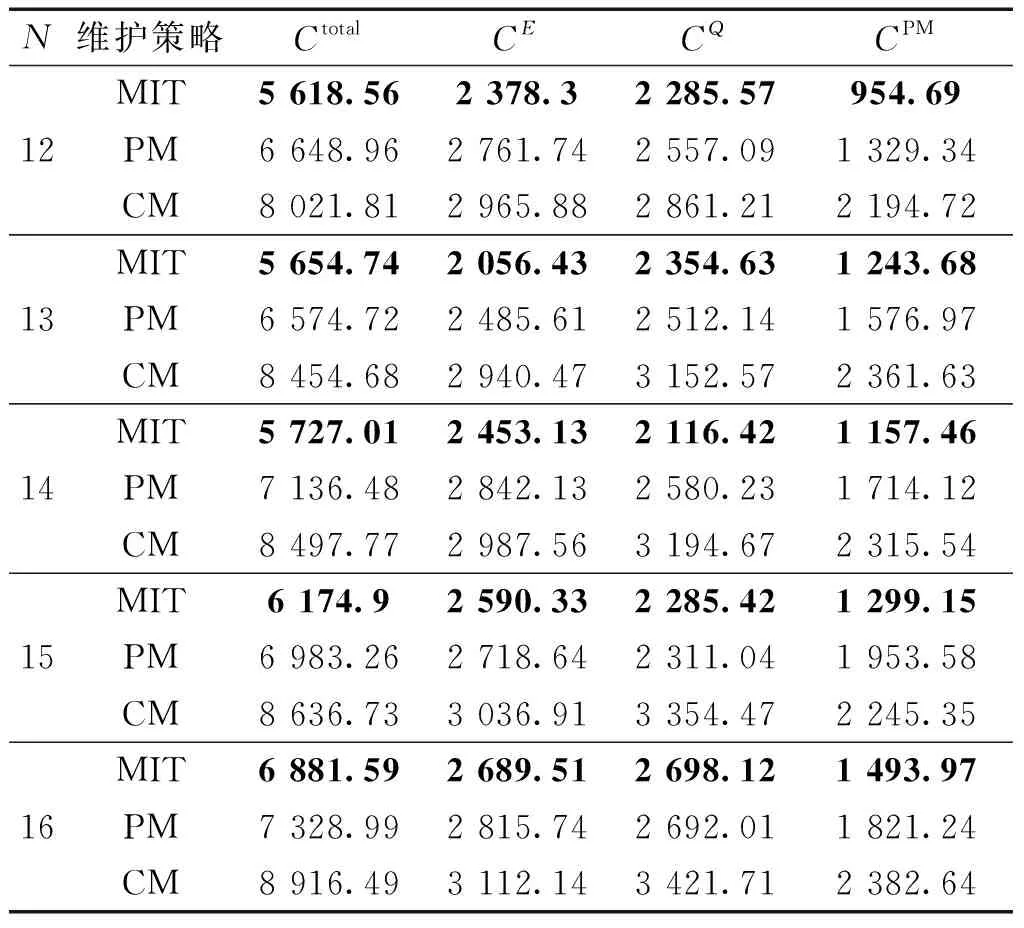
在串行生產系統中,若某設備經過時間tp后其劣化量到達預防性維護閾值Xp,則需要對其采取預防性維護。由假設3)可知系統中存在能耗約束ξe以及質量約束ξq,這分別對應了能耗控制閾值Xe以及質量控制閾值Xq,從而系統中存在3類維護閾值Xp、Xe、Xq,根據假設5)其中預防性維護閾值最大,即max{Xe,Xq} 由于某設備的運行能耗以及產出質量均基于設備劣化量X(t)而改變,當設備劣化量X(t)遞增至預防性維護閾值Xp時,由于Xp大于其余2類閾值,所以此時設備的能耗水平以及次品率已經超出了能耗約束ξe以及質量約束ξq。這意味著當給定約束ξe、ξq時,相應的設備維護閾值Xe、Xq也隨之確定,接下來給出該閾值的計算方法: 1)能耗控制閾值。 對于給定的能耗約束0<ξe<1: (10) 其對應的能耗控制維護閾值Xe為: Xe=f-1(K(Xi(t))) (11) 2)質量控制閾值。 對于給定的質量約束0<ξq<1: ξq=p0+Xw[1-e(-λ·Xqθ)] (12) 其對應的質量控制維護閾值Xq為: (13) 3)多指標集成維護閾值。 基于上述概念,在維護時綜合考慮生產中的能耗約束與產品約束,定義一臺設備的MIT為: MIT={Xp,min{Xe,Xq}} (14) 式中Xp為設備的預防性維護閾值,Xe、Xq為系統的能耗控制閾值與質量控制閾值,利用MIT來決策系統中的待維護組并輸出,方法是一旦某臺設備到達其預防性維護閾值Xp時后,此時訪問生產系統中其余設備的MIT,若由設備劣化量超出MIT中的規定閾值X(t)≥min{Xe,Xq},則將其加入待維護組G={Gp,Ge,Gq}中,待維護組由3類設備組成,分別是有預防性維護需求的設備Gp,以及能耗或質量不滿足約束的設備Ge、Gq。 根據假設5),預防性維護閾值最大,即Xe,Xq均小于Xp,這體現了劣化量是預防性維護的主要指標,能耗與質量則作為次要指標。如此假設的目的是當系統發生劣化需要維護時,一定能保證對系統的能耗以及產品質量的集成控制。換而言之,由劣化觸發的維護活動占主導地位,其余2類指標(能耗、質量)觸發的維護活動為機會維護。MIT將設備的劣化程度、設備能耗、產品質量集成到同一個維護框架中,實現了在生產過程中對這3類指標的集成控制。 由TOC理論可知,生產系統的產出與損失取決于瓶頸設備。由于緩沖區的存在,某臺設備的停機事件可能不會引發瓶頸設備的停機,因而不會對生產系統造成永久生產損失。如果能利用此類停機事件對其余設備進行機會維護,便能有效節約能源成本,這就是節能機會窗機制的核心思想。 定義1節能機會窗(energy saving window, ESW):假設系統中有一組設備G={Gp,Ge,Gq}需要進行停機維護,定義ESW為維護組內某臺設備停機而不引起瓶頸設備Mk產生永久生產損失的最長的時間窗口長度。 ESWm(t)=sup{d≥0: s.t. ?T*(d)} (15) 只有當停機時間d超出節能機會窗時才會導致瓶頸機的永久生產損失: (16) 如果機會維護窗內對待維護設備組進行維護,能在節省維護成本的同時節省大量能量。由定義1給出機會時間窗計算方法: ESWi(t)= (17) (18) 當某臺設備i到達預防性維護閾值后,進入維護周期,對總成本進行計算: (19) 2)生成i組服從伽馬過程的劣化增量,記錄下t時刻設備Mi的劣化總量; 3)記錄最先達到PM閾值的設備為Mm,此時開始維護周期,利用集成維護閾值MIT對其余設備進行判斷,輸出待維護組G; 5)根據式(18)計算此次的維護時間窗ESWi。若維護時長超出節能機會窗,則計算此次生產損失PL=(d-ESWm(t))vk,記錄并更新本次維護成本CPL; 6)更新仿真時長T=T+TPM+Tidel,若T<1 000則跳至步驟3);否則繼續; 7)能耗與質量約束ξe、ξq是否小于1,若是則更新ξe=ξe+0.1,ξq=ξq+0.1,然后跳至步驟3),否則繼續; 8)記錄本次仿真的總成本Ctotal、能源成本CE與質量成本CQ,若是則更新ξe=ξe+0.1,ξq=ξq+0.1,然后跳至步驟3),否則繼續; 9)令預防性維護閾值Xp每次加5,若Xp小于100則返回步驟3),否則結束。 為了驗證提出的維護策略的有效性,接下來通過一個數值實例對所建立的模型進行演示與驗證,并討論在不同約束與維護閾值下對于各項成本的影響。考慮一個由12臺設備與11個緩沖區所組成的串行生產系統,系統的劣化過程服從參數α=0.5,β=1.8的非定態伽馬過程,設定設置仿真時長為1 000,能耗增長系數λe=0.01,狀態改變閾值Xω=65,維護能耗ePM=4,PM的固定與可變成本率cs=1,cv=1.2,各設備的具體參數如表1所示。 表1 串行生產系統中各設備參數 將設備運行能耗根據劣化程度進行非等間隔劃分,取區間劃分因子ηL=0.8,劣化等級數L=5,將每臺設備的運行能耗離散化為5個能耗等級,12臺設備在t時刻的能耗等級如圖4所示。 圖3 蒙特卡洛仿真流程Fig.3 Monte Carlo simulation process 圖4 串行生產系統能耗遞增Fig.4 Increasing energy consumption in serial production system 為提升求解效率,根據Zhou等[4]等將PM閾值的搜索區間確定為[40,95],因為過低的PM閾值會導致頻繁的維護和停機成本,最優成本通常不會在此區間出現,因此舍棄這部分缺乏參考價值的數據,將每個生產周期內所有機器的總維護成本、總能耗成本與總質量損失成本并繪制成圖5。從圖中可以看出,總能耗成本是隨著PM閾值先減后增的,當PM閾值范圍落入[0.4,0.65]時有較多的設備將進入待維護組,導致了維護能耗的增加,因此隨著PM閾值的升高,維護能耗也隨之下降。但是越高的PM閾值系統劣化量也越大,PM閾值范圍落入[0.8,0.95]時運行能耗開始增長;總質量成本是持續遞增的,顯而易見,是由于系統劣化量的增大從而導致次品率的升高,導致了質量成本的增加;總維護成本整體也是先降后升的,因為PM閾值的增大會使得維護次數下降,在PM閾值落入[0.4,0.65]時維護次數的下降導致了維護成本的降低,但是維護成本同時與系統劣化量成正比,后期單次維護成本的增加開始占據主導地位,這導致了總維護成本的先降后升。 圖5 不同維護閾值下各項單位成本的變化Fig.5 Energy consumption cost, quality cost and maintenance cost under different thresholds 圖6給出了能耗約束ξe與質量約束ξq分別從0增大到1相應的總成本變化。可以從圖6看出隨著ξe的增大,總成本總是呈現先減少后增大的趨勢。以ξq=0為例,當能耗約束ξe∈[0,0.6]時,約束的增大使得高能耗機器能夠及時得到維護,降低了機器運行的能源成本,當ξe∈[0.6,1]時,約束的增大導致出現過修的情況,從而加大了總成本,同理ξq的變化趨勢也是出于相似的原因。在本次實驗中,生產系統最優約束組合為ξe=0.3,ξq=0.6,此時的總成本大小為6.743×103。 圖6 不同指標約束下單位總成本的變化情況Fig.6 The total cost under different attribute constraints 為驗證提出維護策略的有效性,將帶有能耗與質量約束的基于MIT的集成維護策略分別與常規預防性維護策略PM以及事后維護策略(corrective maintenance,CM)進行對比,設定預防性維護閾值Xp=70,故障閾值Xf=100,事后維護的維護成本與維護能耗均為預防性維護的1.3倍(CCM=1.3CPM,eCM=1.3ePM),選取不同的設備規模N進行實驗,分別記錄其總成本Ctotal,能耗成本CE及質量成本CQ,如表2所示。可以看到不同設備規模下,事后維護策略CM的各項成本總是最高的,這是由于在CM策略中設備只有到達了故障閾值才進行維護,CM的維護成本高于PM,且CM策略下系統整體劣化程度較高,將引發較高的能耗成本與質量成本;預防性維護策略PM對到達預防性維護閾值Xp的設備進行維護,一定程度上能夠改善系統的總成本,但是沒有關注到系統的能耗以及質量情況;在不同規模機器的仿真中,基于MIT方法的總成本總是所有維護策略中最低的,且其能耗成本CE,質量成本CQ與維護成本CPM也分別為所有策略中最低的,與PM策略相比MIT方法降低了6.01%~15.49%的總成本,與CM策略相比降低了16.02%~29.96%的總成本。此外基于MIT方法的維護策略對于維護成本的優化最為顯著,相對PM策略能夠降低17.97%~32.48%的維護成本,相對CM策略可以降低23.56%~33.23%的維護成本。證明基于MIT的集成維護方法可以有效地對系統的能耗成本與質量成本進行控制,節約維護能耗從而優化系統總成本。 表2 3種維護策略下的各項單位成本Table 2 Cost per unit of time under three strategies 1)以帶中間緩沖區的串行生產系統為研究對象,通過建立多指標集成維護閾值MIT并引入“節能機會窗”機制,提出了一種基于MIT的預防性維護策略,該模型可以有效模擬生產過程中的能耗遞增情況并同時考慮質量損失,填補了以往維護模型中的空白; 2)采用蒙特卡洛仿真算法對不同的能耗約束ξe與質量約束ξq進行搜索,找到最優的約束組合為ξe=0.3,ξq=0.6。 3)探究了不同的維護閾值對能源成本、質量成本與維修成本的影響,基于MIT的集成維護方法相對于PM策略MIT方法降低了6.01%~15.49%的總成本,與CM策略相比降低了16.02%~29.96%的總成本,實驗證明提出的維護策略對于制造企業優化能耗、控制質量以及降低總運營成本具有一定的指導意義和參考價值。2.3 節能機會窗
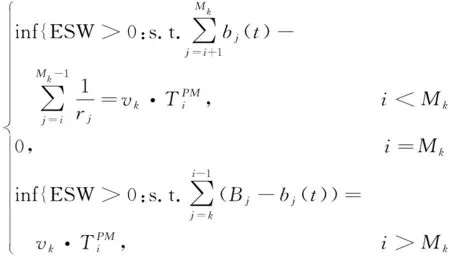
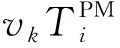
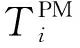
2.4 成本模型
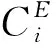
3 維護模型求解
3.1 蒙特卡洛仿真算法
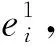
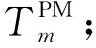
3.2 數值仿真實驗
4 結論

