基于深度學習的水下目標姿態識別

李秀坤， 徐天楊， 嵇守聰

(1.哈爾濱工程大學 水聲技術重點實驗室，黑龍江 哈爾濱 150001； 2.海洋信息獲取與安全工業和信息化部重點實驗室(哈爾濱工程大學)，黑龍江 哈爾濱 150001； 3. 哈爾濱工程大學 水聲工程學院，黑龍江 哈爾濱 150001)

研究水下目標聲散射物理機理，建立散射信號參數與目標屬性之間的函數關系是獲取目標屬性信息的關鍵。根據目標聲散射特性，回波可分為幾何聲散射回波與彈性聲散射回波[1]。聲吶目標回波亮點模型是目標散射回波分析的有效工具[2-3]。結合該模型中的理論，根據不同聲波入射角度下目標聲散射成分的時序關系可以對回波角度進行識別。

分數階傅里葉變換是一種具有良好的脈沖壓縮性能的時頻分析方法[4]，適用于分析具有線性調頻特性的非平穩信號，在主動聲吶目標探測識別中具有的廣泛應用[5]。在發射線性調頻信號的情況下，目標回波具有與發射信號相似的調頻特性，在分數階變換域中回波成分具有最佳變換階數[6]。根據變換關系，利用最佳變換域的結果可以進行信號的參數估計[7]。

基于淺層學習的傳統模式識別方法依賴于人為提取的特征向量，且參數無法進行自學習，對于大樣本、高維數據的分類識別效果有限。深度學習方法克服了傳統方法在高維數據表征能力的不足，根據訓練數據調整參數，提取數據的深層特征，準確地實現分類任務[8]。深度學習方法在水聲領域已得到廣泛地應用。Fischell提取目標回波的幾何散射強度和三維散射場特征，實現對球體和圓柱體目標形狀和成分的分類[9]。多模態深度學習分類識別方法將長短時記憶系統與卷積神經網絡結合，對信號的一維和二維特征并行處理，提高水下目標識別精度[10]。將二階池化與卷積神經網絡相結合，可以從聲信號的時頻表示中獲取目標分類信息[11]。

本文基于聲吶目標回波亮點模型對有限長半球頭圓柱目標聲散射回波信號進行分析，利用分數階傅里葉變換提取不同入射角度下的目標回波特征。將傳統特征與深度學習方法結合，以獲取的特征作為深度學習網絡模型的輸入，通過對網絡結構和參數的優化實現不同入射角度下回波的分類識別。

1 水下目標聲散射機理

目標聲散射是入射聲波與目標作用的結果，聲散射回波中包含目標形狀、尺寸、結構、材質等信息。目標聲散射的求解方法包括嚴格的理論解析解和近似理論解，對簡單形狀的目標，可以將聲散射歸結為波動方程和邊界條件描述的數學物理問題[12]。實際水下目標受限于復雜的形狀以及邊界條件，可采用共振散射理論對聲散射機理和回聲成分和特性進行研究[13]。聲吶目標回波亮點模型理論是在此基礎上發展的一種高頻近似方法，能夠直觀地分析目標回波特性，可以作為聲散射回波處理方法研究的信號模型，符合實際的工程應用。

亮點模型將復雜目標的回波近似為多個子回波疊加的結果，子回波從目標某個等效的散射點產生，這些散射點即為亮點。根據形成機理分為幾何亮點與彈性亮點[13]，其中幾何亮點成分服從線性聲學規律，包括鏡反射和棱角反射。彈性亮點回波包含目標結構和材質信息，產生機理復雜。不同聲散射成分間的時延信息可以作為不同入射角度下目標回波特征提取的依據。

在亮點模型的理論框架下，每個亮點回波信號可以看作入射信號的時延拷貝，對于復雜目標，多亮點的傳遞函數表示為單個亮點傳遞函數的線性疊加：

(1)

式中：Am(r,ω)為第m個幅度因子，與頻率有關；r為聲波入射方向矢量；τm為目標各亮點與接收點間的時延；φm是相位因子。工程中，回波信號可表示為隨不同入射角度變化的參數組合。其中時延因子攜帶了目標的尺寸信息，可以用來分析目標的幾何結構和聲波入射角。

本文研究的目標模型結構示意圖如圖1。根據亮點模型理論，其聲散射回波可以等效為半球和有限長圓柱2個子目標聲散射回波的組合。

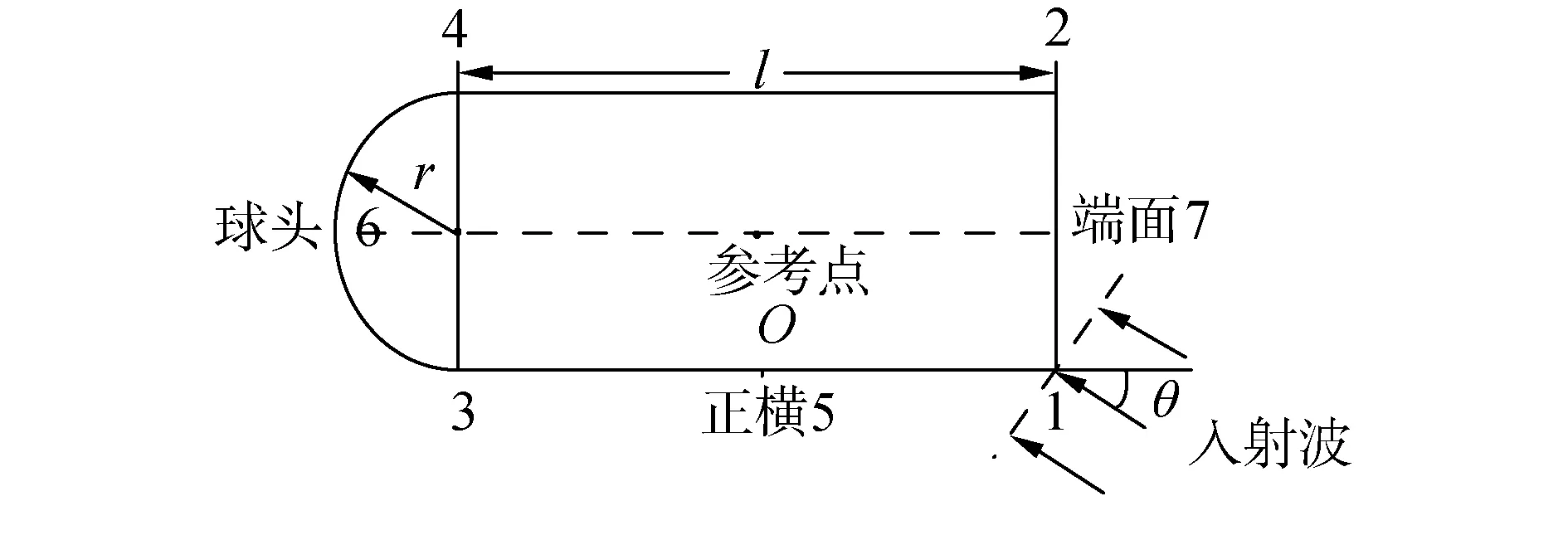
圖1 目標模型結構Fig.1 Schematic diagram of target model

圖1中目標回波主要為棱角波和鏡面反射波，由于目標模型具有對稱結構，簡化分析0～180°內的變化情況。聲波垂直入射目標端面時角度記為θ=0°，正橫入射時記為θ=90°。在圖1中，幾何散射回波主要由圓柱端面、球冠、圓柱正橫以及棱角1、2的回波成分組成，由于目標表面不夠光滑，在3、4處同樣也會產生幾何聲散射回波。在觀察范圍內棱角4處于影區，故棱角散射回波包含棱角1、棱角2和棱角3，鏡反射回波則包含端面正橫7、正橫5和球冠6。不同的聲波入射角度會導致目標幾何散射回波中含有的目標種類和數目顯著變化，在觀測范圍內，亮點出現位置與入射角度關系見表1。

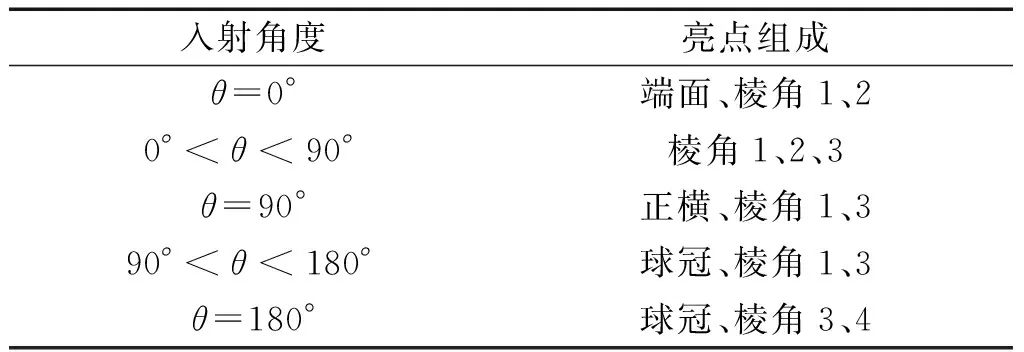
表1 入射角度與亮點關系

結合幅度因子和時延因子對目標模型不同入射角度的幾何回波進行仿真，仿真信號歸一化頻率為0.02～0.08，仿真結果如圖2。圖中不同目標方位角條件下，亮點的成分和數量均有差異，可以作為角度與回波特性之間的映射關系進行深度神經網絡的學習特征。

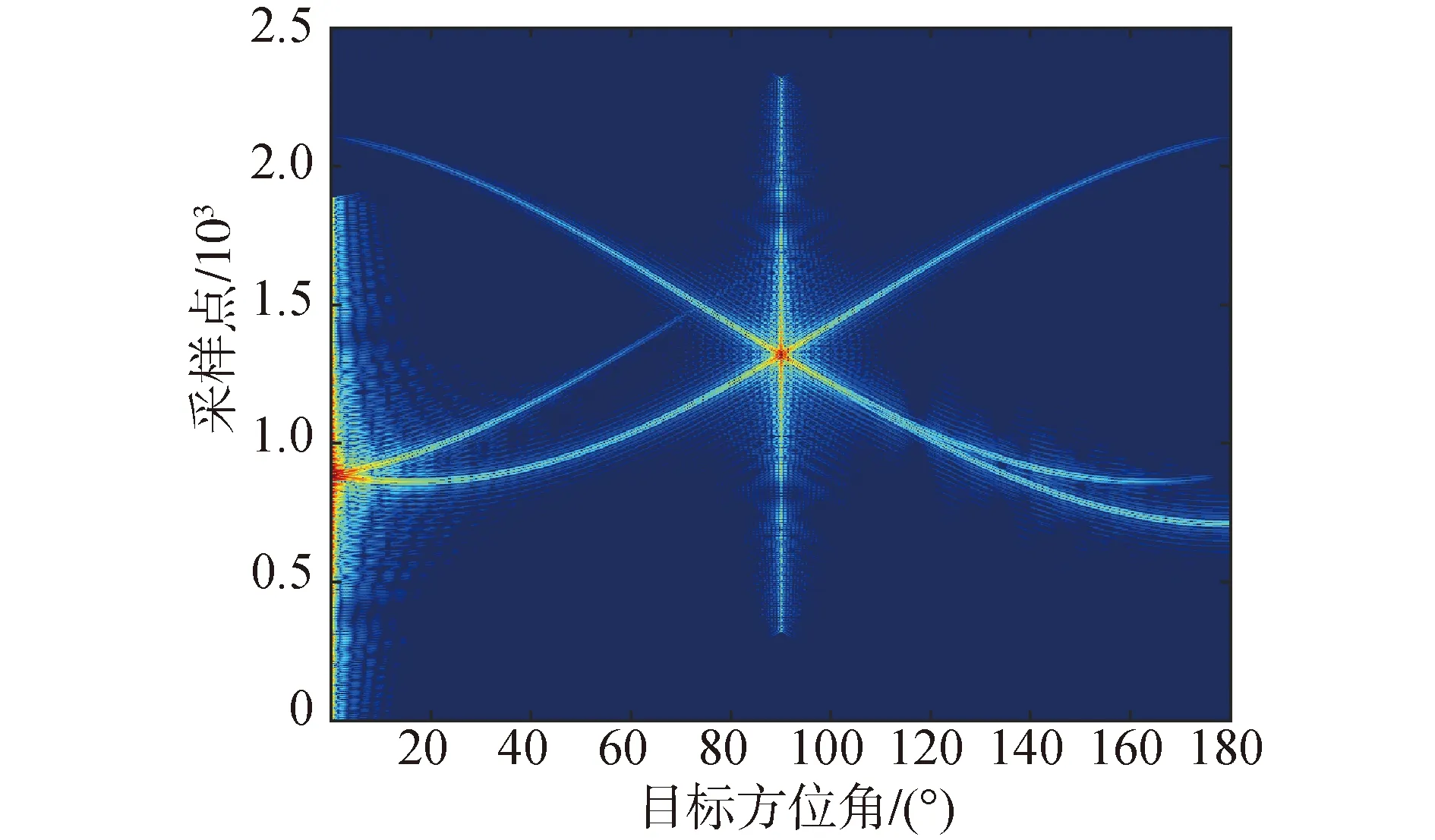
圖2 目標模型幾何亮點回波仿真Fig.2 Simulation of geometric highlight spot echo of target model

2 目標回波特征提取

實際目標探測中，若發射信號的脈寬大于2個相鄰散射成分間的時延，各散射成分在時域上存在混疊，在時域或頻域無法為不同角度回波的識別提供有效特征。時頻分析可以給出信號在時間和頻率2個維度上的信息，其中分數階傅里葉變換可以獲得有效的信號特征。在最佳分數階傅里葉變換域，各聲散射回波分量的時延因子與形成脈沖的位置構成映射關系，通過極大值位置可以計算得到各分量的時延關系[14]，將獲得的時延關系稱為信號的時序結構特征。

2.1 分數階傅里葉變換

根據分數階傅里葉變換的定義，x(t)的p階分數階傅里葉變換可表述為：

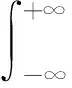
(2)

式中Kp(t,u)為分數階傅里葉變換的核函數：

(3)

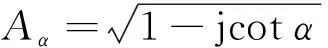
2.2 仿真分析

當坐標旋轉角度對應最佳分數階變換階次，單個亮點回波的最佳分數階傅里葉變換為

F(u)=ATexp[jπT(f0-kτi-ucscα)]·

sinc[πT(f0-kτi-ucscα)]

(4)

式中：T為發射信號長度；f0為信號初始頻率；k為調頻斜率；τi為第i個亮點分量的時延，可以看出單亮點的最佳分數階傅里葉變換為sinc函數形式，其幅度極大值及其在分數階域對應的位置為：

(5)

umax=(f0-kτi)sinα

(6)

式中：A0為發射信號的幅度；Ai為回波信號中第i個亮點的幅度。對于不同回波成分，經分數階傅里葉變換后的脈沖幅值大小取決于幅度因子，sinc函數位置取決于時延因子。從時頻投影的角度來看，變換后的信號在時頻平面為一條斜線，在最佳分數階傅里葉變換域的投影結果存在峰值。在(p,u)平面上，與發射信號參數對應的最佳階次附近，通過搜索最大值的方法確定最佳分數階傅里葉變換階次，獲得回波信號在最佳分數階傅里葉變換域的時序結構特征。

仿真線性調頻信號，脈寬1 000點，歸一化頻率0.02～0.08，聲波入射角度分別為θ=60°和θ=120°，根據仿真信號參數計算可知，最佳分數階次為-0.886 6，在最佳分數階次附近的[-1.126 6,-0.636 6]范圍內得到的分數階傅里葉變換結果如圖3所示。選取最佳分數階次下的分數階傅里葉變換結果如圖4所示。利用最佳分數階次下得到的分數階傅里葉變換能夠獲得不同入射角度下目標回波精細的時序結構。2個角度下的時序結構中均出現5個峰值，其中θ=60°時3個幾何散射回波對應棱角1、2、3，第4、第5個峰值為彈性環繞波。θ=120°時第1個峰值對應球冠的鏡反射回波，第2個峰值對應棱角3的散射回波。由于2個亮點時延間隔很小，導致峰值接近重疊。同時2個角度下幾何散射成分對應峰的聚集性都比較好，彈性環繞波對應的峰值相對于幾何散射成分較小且聚集性較差。不同聲波入射角度下，各散射成分對應的幅度極大值具有顯著差異，各亮點成分的時延也具有差異性。目標回波在分數階域的時序結構在不同入射角度下的差異，可以作為不同入射角度回波的識別特征。

圖3 仿真目標回波的分數階傅里葉變換Fig.3 Fractional Fourier transform of simulated target echo

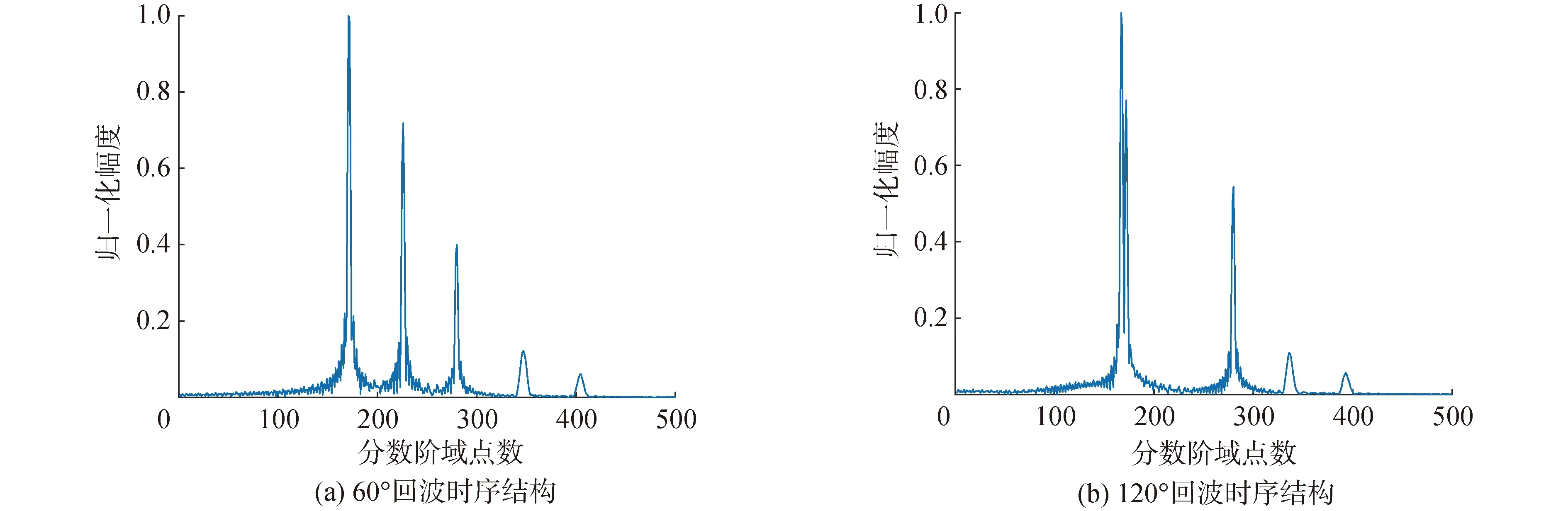
圖4 仿真目標回波的分數階傅里葉域時序結構Fig.4 Time series structure of simulated target echo in fractional Fourier domain

3 網絡構建與實驗數據處理

3.1 深度學習網絡構建

長短期記憶神經網絡(long short-term memory networks, LSTMs)是循環神經網絡(recurrent neural networks, RNN)的一種特殊形式[15]。循環神經網絡是為有效處理時間序列數據而設計的，時間序列數據的顯著特征是相鄰信號幀與長距離幀之間特征存在密切關聯，因此循環神經網絡的神經元被設計成具有環路的網絡結構，其輸出由存儲過去信息的狀態變量與當前的輸入共同決定，是一類具有短期記憶能力的神經網絡。循環神經網絡可以將時間序列信息間的特征保存在網絡的隱藏狀態中，完成對序列信號的動態建模。但當輸入序列比較長時，按照時間的逆序將錯誤信息逐步向前傳遞時會存在梯度爆炸和消失問題，引入了門控機制的LSTMs可以有效地解決這個問題。

長短期記憶神經網絡中引入了遺忘門Ft、輸入門It和輸出門Ot的3個門結構，以及用于記錄額外的信息、進行線性循環信息傳遞的記憶細胞Ct[15]，長短期記憶神經網絡的內部結構如圖5。

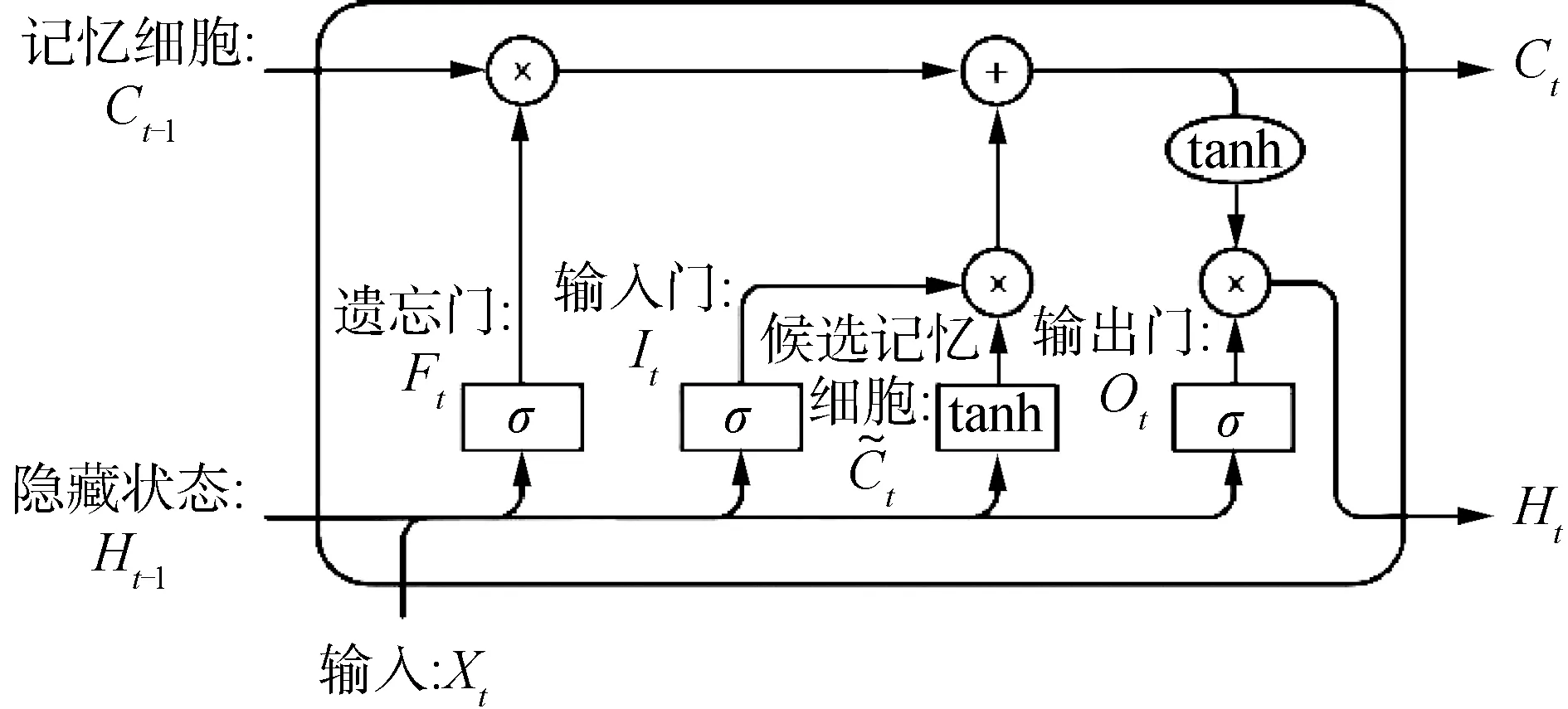
圖5 LSTMs結構Fig.5 Structure of LSTMs

3.2 實驗數據處理

數據源自消聲水池中模擬自由場環境對目標散射回波的測量實驗。實驗水池六面鋪設吸聲尖劈，在工作頻率內能夠減弱由反射引起的多途，避免目標散射回波的干擾。實驗系統布放如圖6所示。目標模型與收發合置換能器處于相同水平位置，發射信號歸一化頻率為0.02～0.08，脈寬為1 000采樣點，目標由機械系統控制勻速旋轉，信號發生與采集裝置由同步信號控制，目標反向散射回波信號經基陣接收后由信號采集器存儲。

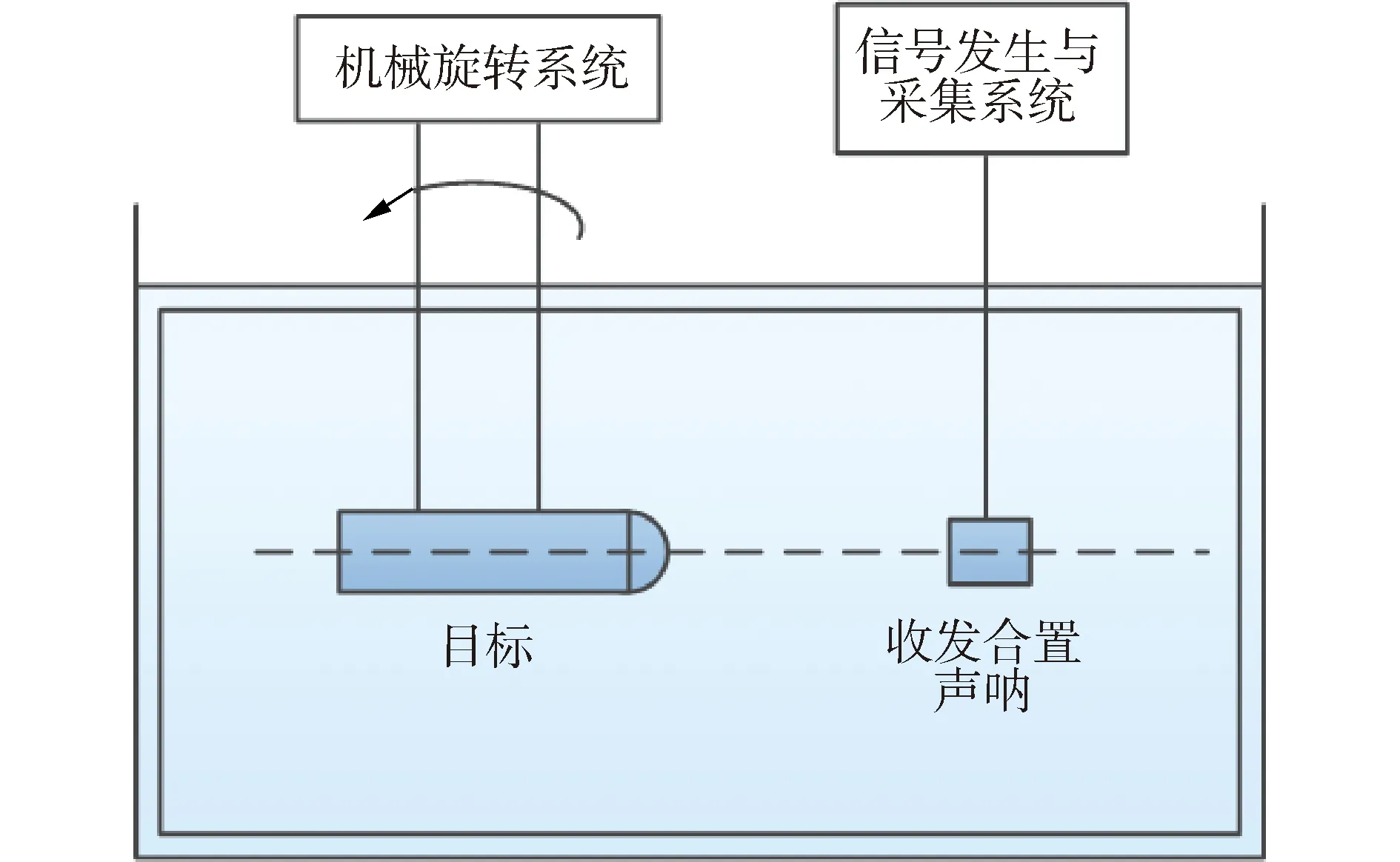
圖6 實驗系統布放Fig.6 The setup of the experiment

考慮水平旋轉情況下，全角度目標反向散射信號的采集，定義聲波自半球一側沿殼體軸向入射為θ=0°，從平面一端為θ=180°，而正橫入射為θ=90°。

在最佳分數階次下，利用分數階傅里葉變換獲取不同入射角度下目標回波的時序結構，作為不同入射角度回波的識別特征。在0～180°內，每間隔15°，共13類角度的目標回波信號求取相應的最佳分數階傅里葉域的時序結構特征，圖7中為觀測范圍內典型角度的時序結構示意圖。

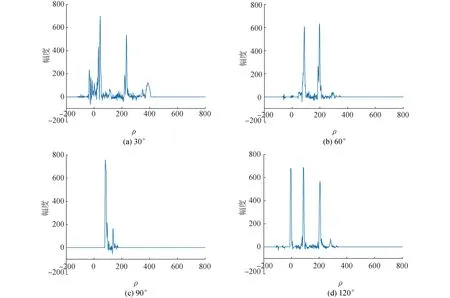
圖7 0°～180°范圍內最佳分數階域時序結構Fig.7 Optimal time sequence structure in fractional Fourier domain from 0°～180°

實際探測中存在環境干擾和聲場分布不均勻等問題，目標回波的波形可能產生畸變。對不同時刻接收到的回波，分數階傅里葉變換所得到結果不同，時序結構的特征會隨之改變。并且對不同角度下彈性環繞波間的時延研究，缺乏明確函數關系的量化，對高維時序結構數據進行降維處理會導致特征信息的丟失。這些問題都將增加分類識別的難度，深度學習中的循環神經網絡適合處理此類時間序列數據。循環神經網絡可以將時間序列信息間的特征保存在網絡的隱藏狀態中，學習復雜的函數映射關系，完成對序列信號的動態建模。

利用分數階傅里葉變換提取不同入射角度下目標回波在最佳分數階域的一維時序結構，采用LSTMs進行訓練學習，與采用頻譜結構作為輸入數據訓練得到的模型進行對比，訓練所得模型驗證集的混淆矩陣如圖8。混淆矩陣表明模型預測過程中，對哪一部分產生混淆，用以判斷模型分類預測的優劣。文中實現13類標簽的分類任務，混淆矩陣的尺度為13×13，混淆矩陣在對角線上的值越大，表明模型的分類性能越好。

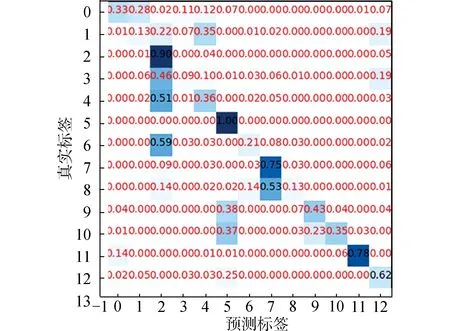
圖8 頻譜結構-LSTMs的混淆矩陣Fig.8 Confusion matrix of spectrum structure- LSTMs

使用頻譜結構數據構建模型的混淆矩陣表明，在多數角度下的模型分類性能表現不佳。損失-準確率變化曲線以及ROC曲線(受試者操作特性曲線)如圖9所示。損失-準確率曲線描述模型的傳播損失和準確率隨訓練期數(epoch)的變化規律，曲線評價模型(receiver operating characteristic，ROC)在不同閾值下的表現情況，曲線的橫、縱坐標分別表示假陽率和真陽率。(area under curve，AUC)表示ROC曲線下方面積，用來表征模型正確預測為正例的值高于將其預測為負例的值的概率，越接近1則模型性能越好。

圖9描述了模型整體性能以及模型對每一類樣本的識別能力。圖9(a)中，隨著訓練期數的增加，訓練集的誤差呈下降趨勢，但訓練集的準確率在93%的基礎上只有小幅度的上升，且驗證集的誤差表現不穩定。圖9(b)中AUC值普遍較小，說明頻譜結構數據仍不足以作為表征不同角度回波的特征。這是因為回波各散射成分存在相似的調頻性質，而幾何散射回波的頻譜范圍更廣，導致其完全覆蓋了彈性回波的頻譜，深度神經網絡也難以學習到深層特征。

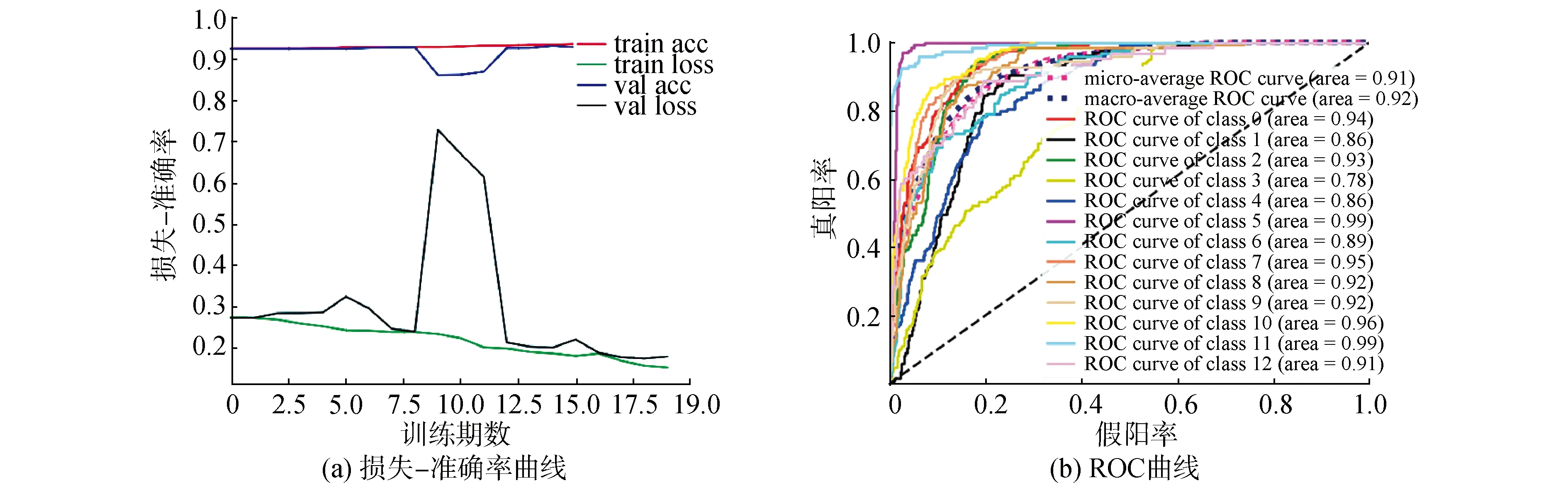
圖9 頻譜結構-LSTMs模型性能Fig.9 Performance of spectrum structure-LSTMs

將分數階域下的時序結構作為LSTMs的輸入數據，訓練所得模型的驗證集混淆矩陣如圖10。

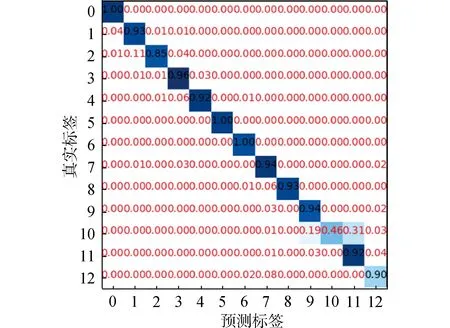
圖10 FRFT-LSTMs的混淆矩陣Fig.10 Confusion matrix of FRFT-LSTMs

圖10中混淆矩陣結果表明，利用時序結構訓練得到的模型，其混淆矩陣對角線上的值接近100%，在150°時有一定錯誤分類的概率，但分類錯誤樣本主要集中在與樣本臨近的角度，相比于頻譜結構數據下混淆矩陣所呈現出的模型分類性能，采用FRFT-LSTMs的模型分類性能具有顯著增強。進一步采用損失-準確率變化曲線以及ROC曲線對模型進行評估，結果如圖11所示。

圖11(a)中損失-準確率曲線表明，模型在第2次迭代后損失準確率曲線即得到了收斂，訓練集和驗證集的準確率穩定在98.92%和98.53%；圖11(b)中的ROC-AUC曲線表明，AUC值均接近1，眾多評估指標表明FRFT-LSTMs的模型可以實現對不同角度回波的精準分類識別。頻譜結構-LSTMs和FRFT-LSTMs兩種模型的詳細評估指標如表2所示。

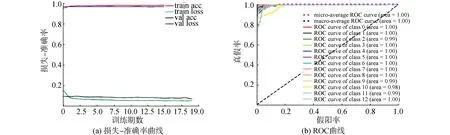
圖11 FRFT-LSTMs模型結果Fig.11 Results of FRFT-LSTMs

表2 模型各項評估指標Table 2 Evaluation indicators of the model

與頻譜結構-LSTMs模型相比，FRFT-LSTMs模型在上述評估指標中均有更佳的性能表現。將分數階域下時序結構的特征作為LSTMs的輸入數據，并與使用頻譜結構數據的LSTMs模型進行對比，FRFT-LSTMs的識別準確率達到了98.53%。通過調節優化網絡參數，構建了2種對水下目標回波角度識別穩定、精確的深度神經網絡模型。

4 結論

1)本文基于亮點模型理論，利用分數階傅里葉變換對不同入射角度下的水下目標回波數據進行時序特征提取，獲得與聲波入射角度相關的目標回波時序結構。通過構建深度學習神經網絡，將時序結構特征作為LSTMs網絡的輸入進行訓練，實現對不同聲波入射角度下目標回波的識別。

2)與采用目標信號頻譜結構作為輸入特征的模型進行對比，采用LSTMs的深度神經網絡模型的識別率可達98.53%。綜合模型查準率、召回率、AUC等指標，FRFT-LSTMs深度學習模型性能均優于傳統頻譜結構-LSTMs。實驗數據處理結果表明，FRFT-LSTMs網絡模型可以實現實驗條件下對水下目標姿態的精準分類與識別。