CaputoΔ型分?jǐn)?shù)階時(shí)間尺度Noether 定理1)
田 雪 張 毅
* (南京理工大學(xué)理學(xué)院,南京 210094)
? (蘇州科技大學(xué)土木工程學(xué)院,江蘇蘇州 215011)
引言
分?jǐn)?shù)階微積分幾乎和整數(shù)階微積分同時(shí)存在,它的導(dǎo)數(shù)和積分的階數(shù)可以是任意數(shù)[1].由于分?jǐn)?shù)階微分方程具有獨(dú)特的能力來描述自然現(xiàn)象的共同特征?異常行為和記憶效應(yīng)[2],因此分?jǐn)?shù)階微分方程能比整數(shù)階微分方程更準(zhǔn)確地描述許多實(shí)際問題.分?jǐn)?shù)階微分方程理論是數(shù)學(xué)的一個(gè)重要分支,包括連續(xù)分?jǐn)?shù)階微分方程和離散分?jǐn)?shù)階差分方程.在過去的數(shù)十年里,分?jǐn)?shù)階微分方程理論得到了廣泛的普及和應(yīng)用[3-8],但這些連續(xù)分?jǐn)?shù)階微分方程和離散分?jǐn)?shù)階差分方程是被分開研究的.1988 年Hilger[9]發(fā)現(xiàn)了離散系統(tǒng)和連續(xù)系統(tǒng)之間有許多相似之處,因此提出了一個(gè)關(guān)于微分方程和差分方程的統(tǒng)一理論?時(shí)間尺度.隨后,Bohner 等[10-12]意識(shí)到時(shí)間尺度微積分彌合了連續(xù)和離散系統(tǒng)之間的差距,這個(gè)統(tǒng)一的方法意味著在復(fù)雜的新模型中可以考慮更多的變量.不僅如此,當(dāng)時(shí)間尺度為T=qN0(q>1,N為自然整數(shù)集)或T=qZ∪{0} 時(shí),時(shí)間尺度上的微分方程可以表示成在量子理論中有著重要應(yīng)用的q差分方程[11].因此,利用不同的時(shí)間尺度T,分?jǐn)?shù)階時(shí)間尺度微積分可以同時(shí)處理連續(xù)、離散和量子分?jǐn)?shù)階微積分.例如,取T=R (R 為實(shí)數(shù)集)時(shí),分?jǐn)?shù)階時(shí)間尺度微分方程則成為[1]中經(jīng)典的分?jǐn)?shù)階微分方程;當(dāng)T=Z (Z 為整數(shù)集)時(shí),其分?jǐn)?shù)階時(shí)間尺度微分方程與文獻(xiàn)[6]中步長(zhǎng)為1 的離散分?jǐn)?shù)階差分方程是一致的;若T=qN0(q>1),其微分方程則成為文獻(xiàn)[7]中的離散分?jǐn)?shù)階q差分方程.近年來,分?jǐn)?shù)階時(shí)間尺度微積分已被應(yīng)用于動(dòng)力學(xué)方程[13]、最優(yōu)控制[14]等領(lǐng)域.雖然力學(xué)系統(tǒng)的分?jǐn)?shù)階Noether 定理和時(shí)間尺度Noether 定理被廣泛研究與應(yīng)用,但分?jǐn)?shù)階時(shí)間尺度Noether 定理是一個(gè)新的研究課題[15].
眾所周知,Noether 定理揭示了對(duì)稱性和守恒量之間的內(nèi)在關(guān)系[16].在群的無限小變換下作用量的不變性(Noether 對(duì)稱性)意味著沿著系統(tǒng)的動(dòng)力學(xué)真實(shí)運(yùn)動(dòng)軌道上存在一個(gè)守恒量(Noether 守恒量).相比牛頓力學(xué)和Lagrange 力學(xué),運(yùn)用Noether 對(duì)稱性可以找到除了能量守恒、動(dòng)量守恒或動(dòng)量矩守恒之外更多的且相互獨(dú)立的守恒量[17].因此,近些年人們致力于研究力學(xué)系統(tǒng)的Noether 定理[18-25].而利用時(shí)間尺度理論得到的Noether 定理,通過選擇不同的尺度可同時(shí)表示連續(xù)時(shí)間變量、離散時(shí)間變量甚至分段時(shí)間變量的Noether 定理.
2004 年Bohner[26]研究了Δ導(dǎo)數(shù)的時(shí)間尺度變分問題,建立了時(shí)間尺度Lagrange 方程.此后,有關(guān)時(shí)間尺度變分原理和時(shí)間尺度Lagrange 方程的理論不斷得到完善[27-30],為研究時(shí)間尺度Noether 定理奠定了基礎(chǔ).2008 年Bartosiewicz 和Torres[31]分別在特殊無限小變換和一般無限小變換的情況下研究了時(shí)間尺度的Noether 定理.隨后,Bartosiewicz 等[32]給出了Δ導(dǎo)數(shù)的時(shí)間尺度第二類Lagrange 方程,并利用該方程證明了文獻(xiàn)[31]中的Noether 定理.之后,各種力學(xué)系統(tǒng)的時(shí)間尺度Noether 定理被建立,如最優(yōu)控制問題[33]、非保守系統(tǒng)[34-36]、非完整系統(tǒng)[37-38]、Hamilton 系統(tǒng)[39-40]、Birkhoff 系統(tǒng)[40-42]、時(shí)滯系統(tǒng)[43-44]等.然而,最近Anerot 等[45]指出文獻(xiàn)[32]中所推導(dǎo)的時(shí)間尺度第二類Lagrange 方程是錯(cuò)誤的.因此,在上述列舉的文章中,利用該方程得到的力學(xué)系統(tǒng)的Noether 定理其正確性有待商榷.Anerot 等[45]利用一種廣義Jost 方法來研究 ? 導(dǎo)數(shù)時(shí)間尺度遷移和非遷移系統(tǒng)的Noether 定理,并且用了一些算例來證明他們的結(jié)果.同樣,Cresson 等[46]將Jost 方法推廣到分?jǐn)?shù)階理論,建立了分?jǐn)?shù)階Noether 定理,并給出了一些應(yīng)用和仿真.本工作利用分?jǐn)?shù)階時(shí)間尺度Hamilton 原理,推導(dǎo)了CaputoΔ型分?jǐn)?shù)階時(shí)間尺度Lagrange 方程,在一般無限小變換下利用廣義Jost 方法建立了CaputoΔ型的分?jǐn)?shù)階時(shí)間尺度Noether 定理.文末對(duì)分?jǐn)?shù)階時(shí)間尺度Kepler 問題和線性振動(dòng)系統(tǒng)進(jìn)行模擬,說明了定理的正確性.
1 預(yù)備知識(shí)
設(shè)T是一時(shí)間尺度,t∈T,定義前跳算子σ:T→T為 σ(t)=inf{s∈T:s>t},后跳算子ρ:T→T為ρ(t)=sup{s∈T:s
定義1設(shè)T是一時(shí)間尺度且Tκ=T,定義右連續(xù)函數(shù)hα:T×T→R,α≥0 為[48]
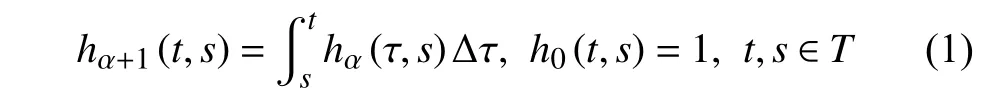
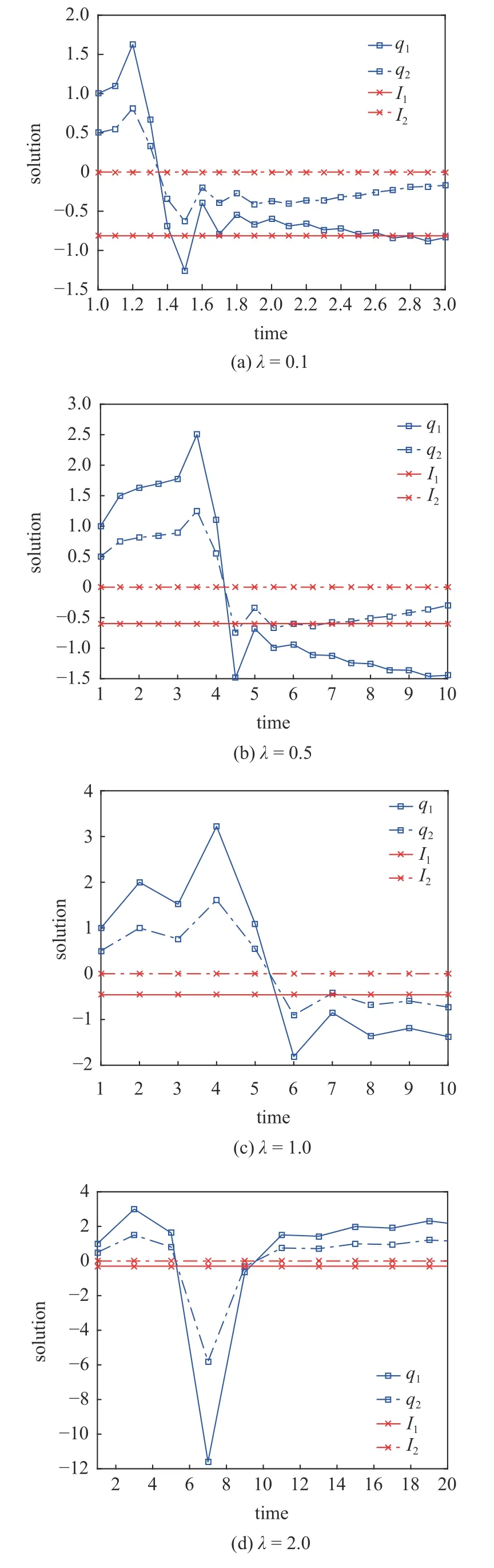
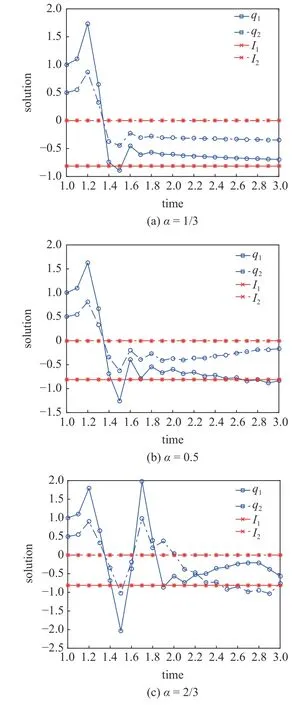
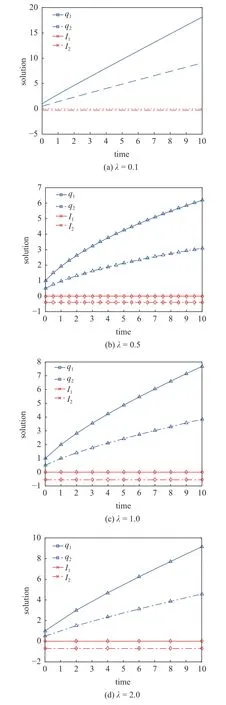
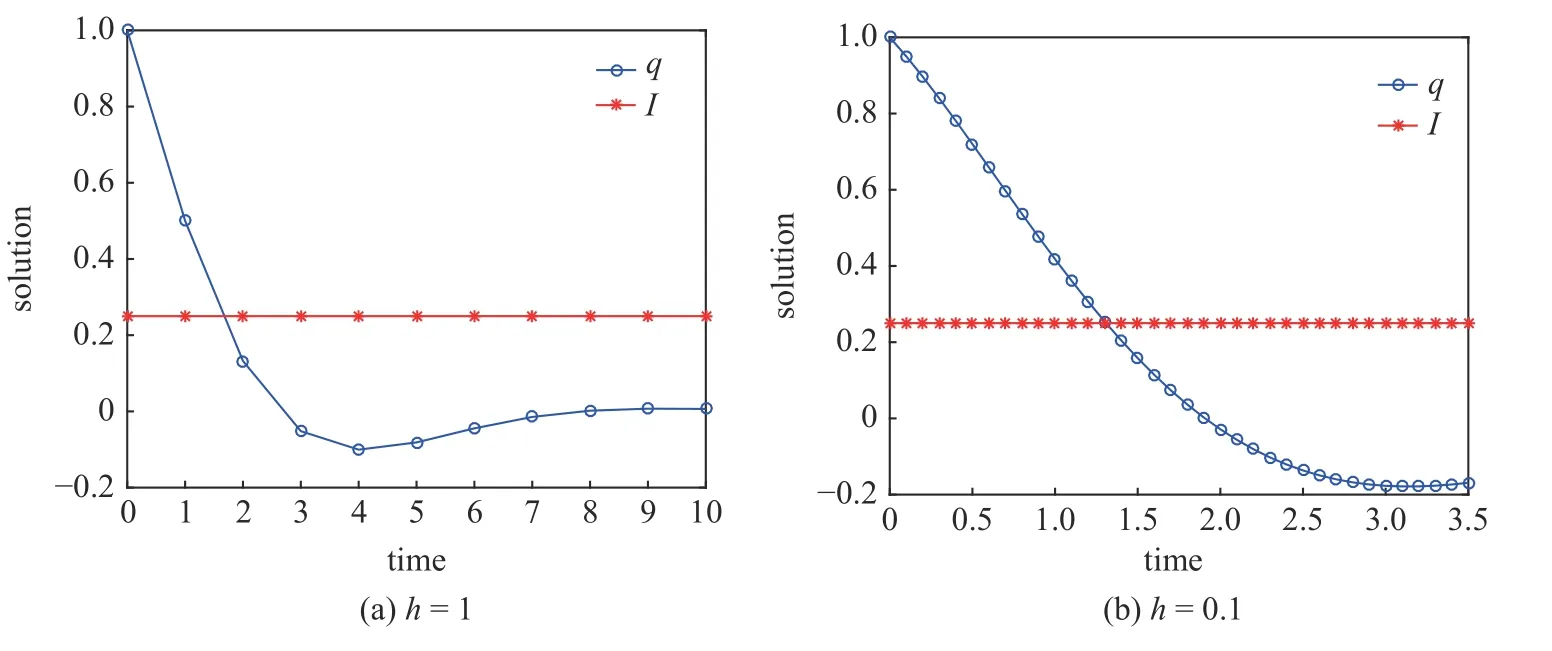
定義2設(shè)T是一時(shí)間尺度,函數(shù)f:[a,b]?R,其中,α≥0,a,b∈R,a 右Riemann-Liouville 分?jǐn)?shù)階Δ積分為 注1:若T=R,有,則 式(4)和式(5)是傳統(tǒng)的左、右Riemann-Liouville分?jǐn)?shù)階積分[1]. 注2:若T=Z,可定義 式(7)和式(8)是離散的左、右Riemann-Liouville分?jǐn)?shù)階積分. 注3:若T=pN0,p>1,令α∈[0,∞)N0,a,t∈T,t≥a,p分?jǐn)?shù)階函數(shù)可定義為 式(10)和式(11)可分別稱為p離散的左、右Riemann-Liouville 分?jǐn)?shù)階積分. 定義3設(shè)T是一時(shí)間尺度,函數(shù)f:T→R,定義,n∈N0,定義左Riemann-Liouville分?jǐn)?shù)階Δ導(dǎo)數(shù)為[47] 右Riemann-Liouville 分?jǐn)?shù)階Δ導(dǎo)數(shù)為 注4:若 α<0,可定義 注5:假設(shè) α≥0,m=+1.若m=0,則有 若m=1,則有 定義4設(shè)T是一時(shí)間尺度,t∈T,α≥0,定義左Caputo 分?jǐn)?shù)階Δ導(dǎo)數(shù)為[47] 右Caputo 分?jǐn)?shù)階Δ導(dǎo)數(shù)為 注6:若 α∈(0,1),即m=1,則有 當(dāng)f(a)=0時(shí),左Caputo 分?jǐn)?shù)階Δ導(dǎo)數(shù)與左Riemann-Liouville 分?jǐn)?shù)階Δ導(dǎo)數(shù)一致;當(dāng)f(b)=0 時(shí),右Caputo 分?jǐn)?shù)階Δ導(dǎo)數(shù)就與右Riemann-Liouville分?jǐn)?shù)階Δ導(dǎo)數(shù)一致. 同樣地,當(dāng)T=R,式(18)和式(19)則成為傳統(tǒng)的左、右Caputo 分?jǐn)?shù)階導(dǎo)數(shù);當(dāng)T=Z,式(18)和式(19)成為離散的左、右Caputo 分?jǐn)?shù)階導(dǎo)數(shù);當(dāng)T=pN0,p>1,式(18) 和式(19) 則成為p離散的左、右Caputo 分?jǐn)?shù)階導(dǎo)數(shù). 引理1設(shè)函數(shù)f,g:T→R在點(diǎn)t∈Tk是Δ可微的,a,b∈T,則有[10] 若 ω=ν?1:Tˉ →T,則有 其中 νΔ≠0.若f:T→R是右連續(xù)的,并且 ν 的右連續(xù)導(dǎo)數(shù)可微,則有其中a,b∈T. 引理4假設(shè)函數(shù)f,g:T→R,a,b∈T,分?jǐn)?shù)階時(shí)間尺度分部積分公式如下[49] 假設(shè)力學(xué)系統(tǒng)的位形是由n個(gè)廣義坐標(biāo)qk(k=1,2,···,n)確定的.設(shè)分?jǐn)?shù)階時(shí)間尺度系統(tǒng)的作用量為 CaputoΔ型分?jǐn)?shù)階時(shí)間尺度Hamilton 原理為 其滿足交換關(guān)系 和邊界條件 對(duì)式(28)進(jìn)行變分運(yùn)算,得 根據(jù)分?jǐn)?shù)階時(shí)間尺度分部積分公式(26),再由式(30)和式(32),可得 將式(33)代入式(32),則有 由式(22)和式(31),方程(34)可寫為 根據(jù)引理2,可得 在式(36)兩邊對(duì)t求Δ導(dǎo)數(shù),有 方程(37)則是CaputoΔ型分?jǐn)?shù)階時(shí)間尺度運(yùn)動(dòng)微分方程,將它稱為分?jǐn)?shù)階時(shí)間尺度Lagrange 方程. 注7:若 α=1,方程(37) 則成為時(shí)間尺度Lagrange 方程[31] 注8:若T=R,方程(37)則成為Caputo 型分?jǐn)?shù)階Lagrange 方程 注9:若 α=1,T=R,方程(37) 則成為經(jīng)典的Lagrange 方程 引進(jìn)單參數(shù)群的特殊無限小變換 式中 ξk(k=1,2,···,n) 是無限小生成元,ε 是無限小參數(shù). 定義5對(duì)任意的 [ta,tb]?[a,b],ta,tb∈T,若有 則稱Hamilton 作用量式(28)在特殊無限小變換式(41)下是不變的. 判據(jù)1若Hamilton 作用量式(28)在特殊無限小變換式(41)下是不變的,則有 證明:由定義5 可知,對(duì)任意的子空間[ta,tb]?[a,b],條件式(42)都成立,所以有 在式(44)中對(duì) ε 求導(dǎo),再令 ε=0,利用分?jǐn)?shù)階時(shí)間尺度Caputo 導(dǎo)數(shù)的定義和性質(zhì),可得 則記 定理1若Hamilton 作用量(28)在定義5 的意義上是不變的,則存在守恒量 證明:對(duì)式(48)中的I求Δ導(dǎo)數(shù),則有 由分?jǐn)?shù)階時(shí)間尺度Lagrange 方程(37)可知 將式(50)代入式(43),可得 即IΔ=0,因此可證明式(48)是特殊無限小變換下的Noether 守恒量. 注10:若 α=1,定理1 成為特殊無限小變換下的時(shí)間尺度Noether 定理[31] 本節(jié)研究一般無限小變換下的分?jǐn)?shù)階時(shí)間尺度Noether 定理.首先,引進(jìn)單參數(shù) (Δ,T) 可容許投射群[45]的一般無限小變換 式中 ζ,ξk(k=1,2,···,n) 是無限小生成元,ε 是無限小參數(shù). 定義6對(duì)任意的 [ta,tb]?[a,b],ta,tb∈T,若有 則稱Hamilton 作用量式(28)在一般無限小變換式(53)下是不變的. 判據(jù)2若Hamilton 作用量式(28)在一般無限小變換式(53)下是不變的,則有 證明:由定義4 和引理3,可得 由定義6 可知 由于 [ta,tb]是 [a,b] 的任意子空間,則方程(57) 等價(jià)于 在式(58)中對(duì) ε 求導(dǎo),再令 ε=0,得 注11:考慮到 不變性的條件(57)可寫為 接下來,引進(jìn)擴(kuò)展Lagrange 函數(shù)L:R×[a,b]×Rn×R?×Rn→R被定義為 其作用量用SL表示,被定義為 設(shè)時(shí)間尺度束類路徑[45]被定義為 當(dāng)tΔ=1,則有 在 F 上的不變性條件(57)可寫成 在方程(66)中對(duì) ε 求導(dǎo),再令 ε=0,則有 在 F 上可簡(jiǎn)化成如下的方程組 將式(69)代入式(67),得 因此,可得到如下的CaputoΔ型分?jǐn)?shù)階時(shí)間尺度Noether 定理. 定理2若Hamilton 作用量(28)在定義6 的意義上是不變的,則存在守恒量 注12:若 α=1,式(73)成為 注13:若T=R,式(73)成為 例1眾所周知,Kepler 問題是牛頓力學(xué)中最早解決的問題之一,Kepler 系統(tǒng)也是最早發(fā)現(xiàn)的可積系統(tǒng)之一.Kepler 問題仍在研究中,并被廣泛應(yīng)用于各個(gè)領(lǐng)域.Eleonski?等[50]指出分?jǐn)?shù)階Kepler 問題中所有有限運(yùn)動(dòng)的軌道也是封閉的.Anerot 等[45]研究了平面上的時(shí)間尺度Kepler 問題的Noether 定理.在這里,我們考慮定義在上的CaputoΔ型分?jǐn)?shù)階時(shí)間尺度Lagrange 函數(shù) 其表示Kepler 問題中兩個(gè)質(zhì)量為1 的相互作用粒子的Lagrange 函數(shù).其中,用分?jǐn)?shù)階導(dǎo)數(shù)代替了存在能量耗散的運(yùn)動(dòng)的速度.當(dāng)T=R且α=1時(shí),分?jǐn)?shù)階時(shí)間尺度Lagrange 函數(shù)式(79)就是傳統(tǒng)的Kepler 問題.根據(jù)分?jǐn)?shù)階時(shí)間尺度Lagrange 方程(37),可得 考慮到判據(jù)2,可得 這樣,我們可以得到兩組無限小變換的解 由定理2,可以得到兩個(gè)守恒量 如果初始條件滿足q1(1)=1,q2(1)=0.5,v1(1)=1和v2(1)=0.5,考慮在時(shí)間尺度為T=λZ 上研究運(yùn)動(dòng)軌跡q1,q2和守恒量I1,I2.此時(shí)hα(t,s) 則為 令a=0,則t≥1.首先,當(dāng) α=0.5時(shí),分別在 λ=0.1,λ=0.5,λ=1和λ=2的情況下模擬q1,q2,I1,I2的值,得到的結(jié)果如圖1 所示. 從圖1 可以看出,在不同的時(shí)間尺度上,軌跡q1和q2各不同,I1的值也不同,但是I2≡0.這表明在這些初始條件下I2是一個(gè)平凡守恒量.但在不同的時(shí)間尺度上,I1和I2始終是常數(shù),從而驗(yàn)證了定理2 的正確性.I1和I2不僅在不同的時(shí)間尺度上是常數(shù),并且在分?jǐn)?shù)階導(dǎo)數(shù) α 取不同值的情況下也是常數(shù).令λ=0.1,當(dāng) α=1/3,α=0.5,α=2/3時(shí)q1,q2,I1,I2在時(shí)間段 [1,3] 上的值如圖2 所示. 圖1 α=0.5 時(shí) q1,q2 ,I1 ,I2 的值Fig.1 Simulation of q1,q2 ,I1 ,I2withα=0.5 從圖2 可以看出,當(dāng)在同一時(shí)間尺度上而 α 不同時(shí),I1和I2不僅是常數(shù)且其值也沒發(fā)生變化.若α=1,則Kepler 問題的時(shí)間尺度Lagrange 方程為 圖2 λ=0.1 時(shí) q1,q2 ,I1 ,I2在 [1,3] 上的值Fig.2 Simulation of q1,q2 ,I1 ,I2on [1,3]withλ=0.1 從而守恒量為 圖3 證明了當(dāng) α=1時(shí),CaputoΔ型分?jǐn)?shù)階時(shí)間尺度Noether 定理可以簡(jiǎn)化為文獻(xiàn)[45]中的時(shí)間尺度的Noether 定理. 圖3 α=1 時(shí) q1,q2 ,I1 ,I2在 [0,10] 的值Fig.3 Simulation of q1,q2 ,I1 ,I2on [0,10]withα=1 例2由于分?jǐn)?shù)階導(dǎo)數(shù)和積分具有記憶效應(yīng),分?jǐn)?shù)階微積分為描述阻尼材料和黏彈性材料提供了更切實(shí)的模型.以單自由度線性分?jǐn)?shù)階振動(dòng)系統(tǒng)為例,其Lagrange 函數(shù)為 在時(shí)間尺度T={tk=a+kh,k∈N} 上求其Noether 守恒量. 由分?jǐn)?shù)階時(shí)間尺度Lagrange 方程(37),得 若T=R,α=1,方程(91)則成為經(jīng)典的阻尼振子 則可稱方程(91)為分?jǐn)?shù)階時(shí)間尺度阻尼振子.由判據(jù)2,有 方程(93)有解 由定理2,得到守恒量 令a=0,γ=1,α=0.5,h=1,初始位置為q0=1,初始速度為v0=?0.5.當(dāng)t=t0時(shí),I0=?0.125,并且 由此可證明式(95)是一守恒量.若 α=1,此時(shí),時(shí)間尺度上的Lagrange 方程為 其守恒量為 在上述給出的初始條件下,當(dāng)h=1和h=0.1 時(shí),分別給出了q和I在時(shí)間段 [0,10]和 [0,3.5] 的模擬結(jié)果,如圖4 所示. 圖4 α=1 時(shí) q 和 I 的值Fig.4 Simulation of qand Iwithα=1 將分?jǐn)?shù)階理論和時(shí)間尺度理論應(yīng)用到動(dòng)力學(xué)問題的研究中,建立的分?jǐn)?shù)階時(shí)間尺度模型更具有廣泛的應(yīng)用性、更切合實(shí)際問題.結(jié)合分?jǐn)?shù)階微積分和時(shí)間尺度微積分,我們研究了CaputoΔ型分?jǐn)?shù)階時(shí)間尺度Noether 定理.若 α=1,文獻(xiàn)[31]在特殊無限小變換下得到的時(shí)間尺度Noether 定理與我們的定理1 一致,但其一般無限小變換下的Noether 定理卻不能成為文中的定理2.利用文獻(xiàn)[45]中的廣義Jost 方法得到了一般無限小變換下的分?jǐn)?shù)階時(shí)間尺度Noether 定理,并通過算例驗(yàn)證了用該方法得到的守恒量是常數(shù),驗(yàn)證了定理的正確性.進(jìn)一步地說明了運(yùn)用文獻(xiàn)[31]中的時(shí)間重新參數(shù)化技術(shù)處理時(shí)間尺度Noether 定理是存在一些問題的. 分?jǐn)?shù)階時(shí)間尺度Noether 定理為求解復(fù)雜系統(tǒng)的方程提供了一種新方法,當(dāng)然它還需要被進(jìn)一步地研究和完善.在今后的工作中,還可考慮以下幾個(gè)問題. (1) 研究如何將該方法進(jìn)一步拓展到非完整系統(tǒng)和Birkhoff 系統(tǒng)或其他復(fù)雜動(dòng)力學(xué)系統(tǒng). (2) 本工作只研究了Caputo 型分?jǐn)?shù)階導(dǎo)數(shù)和Δ型時(shí)間尺度導(dǎo)數(shù),也可研究其他分?jǐn)?shù)階導(dǎo)數(shù)和時(shí)間尺度導(dǎo)數(shù)以及它們之間的差異. (3) 在實(shí)際問題中,需要討論分?jǐn)?shù)階時(shí)間尺度模型中Noether 守恒量的物理意義. (4) 值得注意的是,由于分?jǐn)?shù)階導(dǎo)數(shù)具有記憶性,一般算法并不適用于分?jǐn)?shù)階微積分,算例僅根據(jù)分?jǐn)?shù)階時(shí)間尺度積分和導(dǎo)數(shù)的定義進(jìn)行計(jì)算的.分?jǐn)?shù)階時(shí)間尺度的保結(jié)構(gòu)算法是一個(gè)新的、艱巨的領(lǐng)域,將是我們今后的主要工作.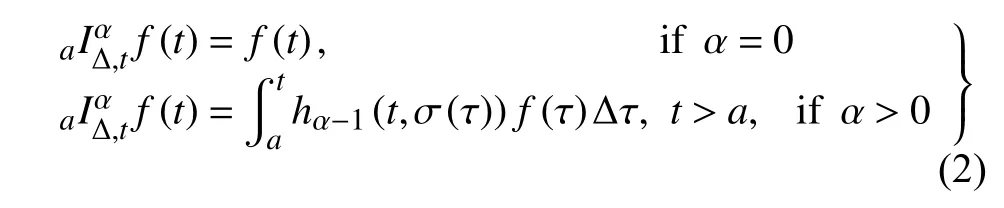
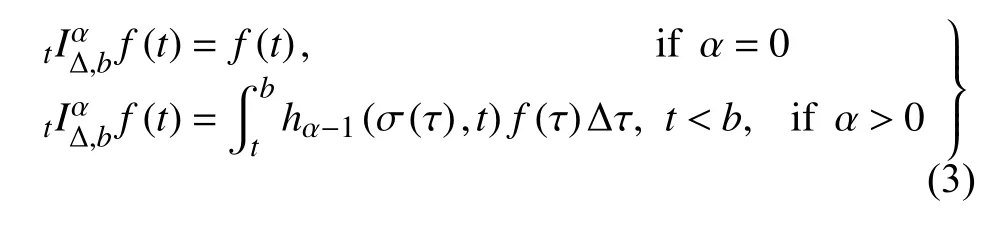
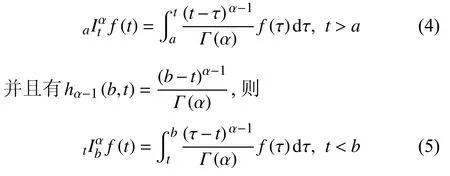


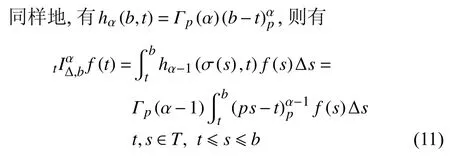
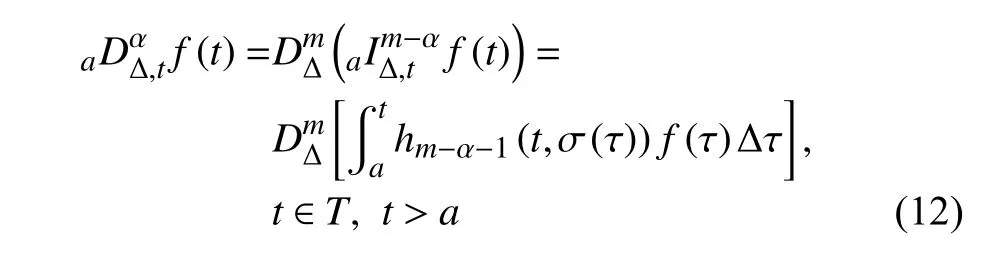
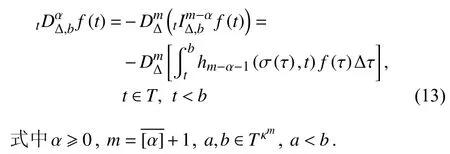
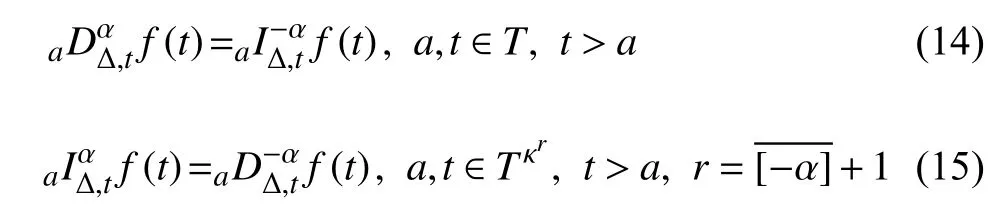
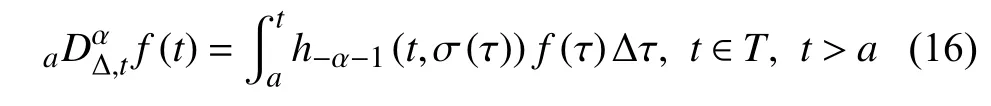
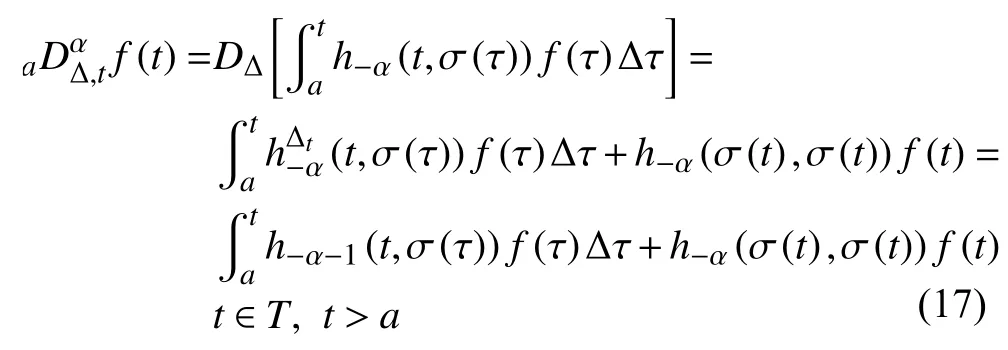
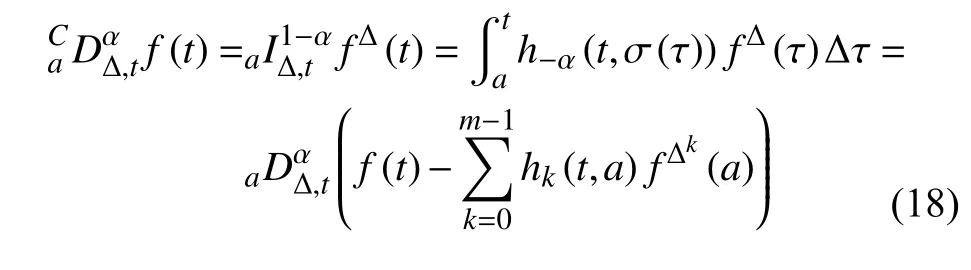
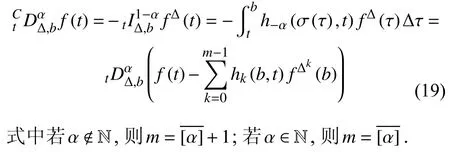


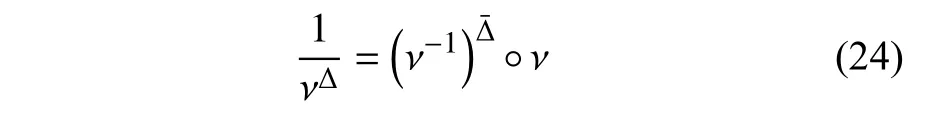
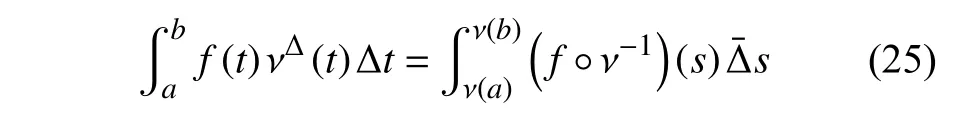
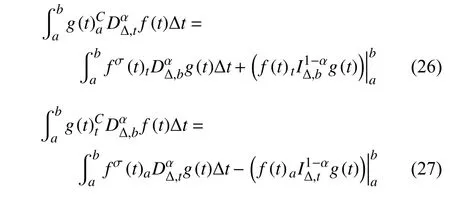
2 CaputoΔ型分?jǐn)?shù)階時(shí)間尺度Lagrange 方程

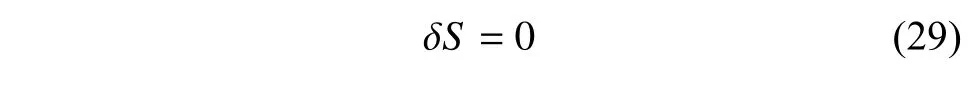
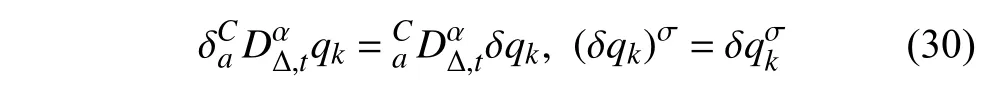
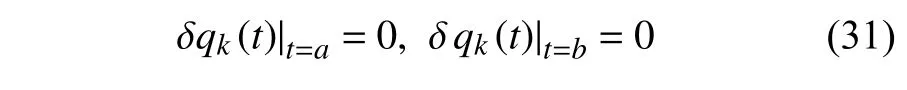
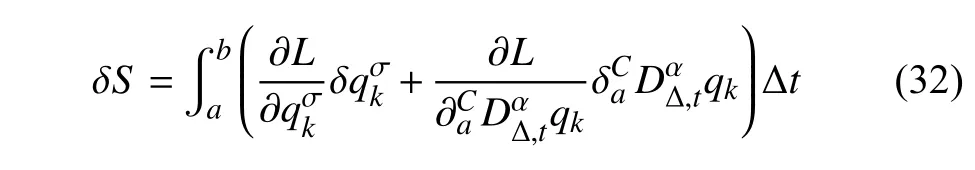

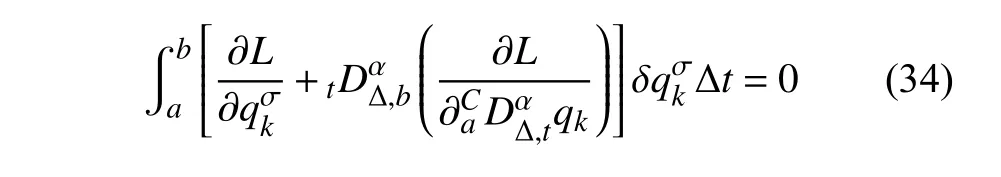

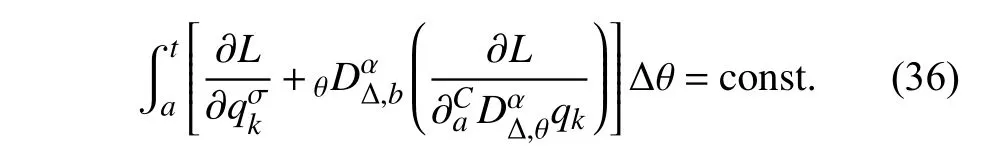
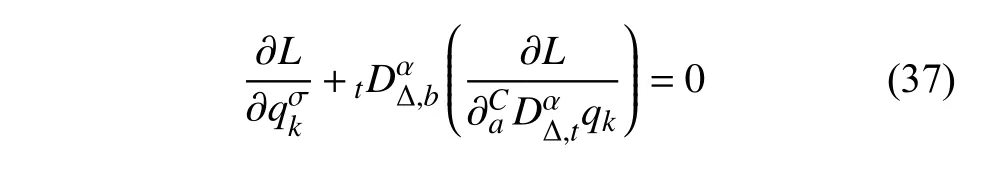
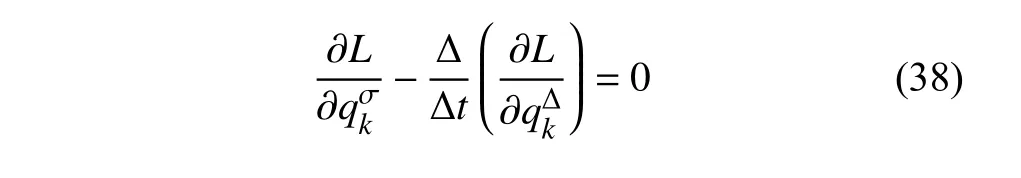
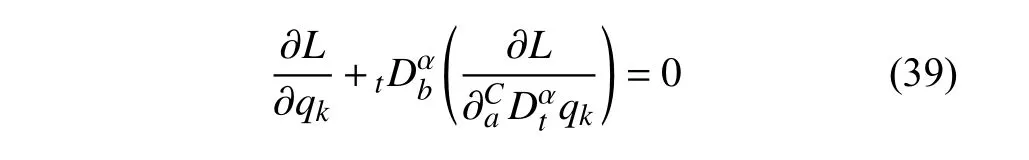
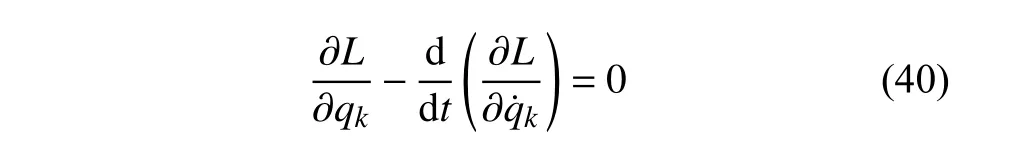
3 特殊無限小變換下的分?jǐn)?shù)階時(shí)間尺度Noether 定理
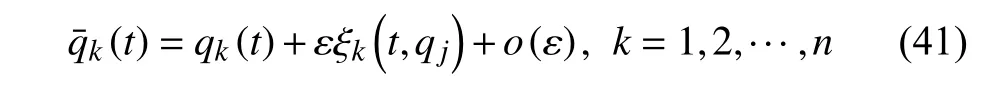
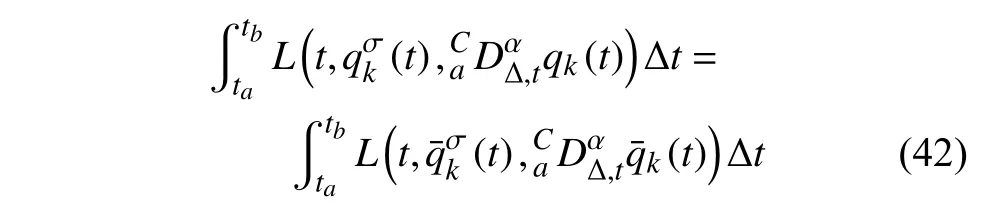
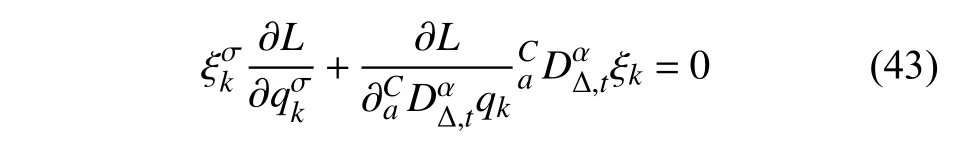
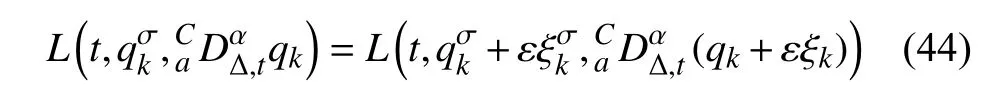

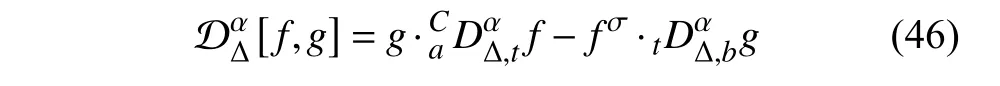
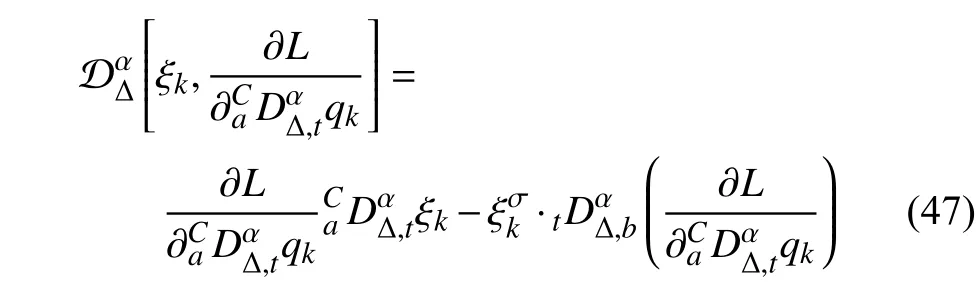
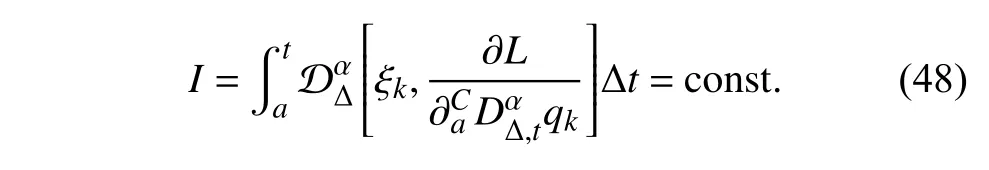
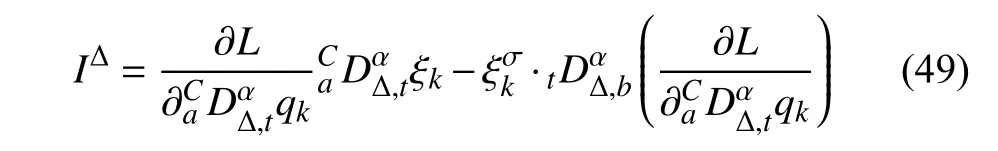
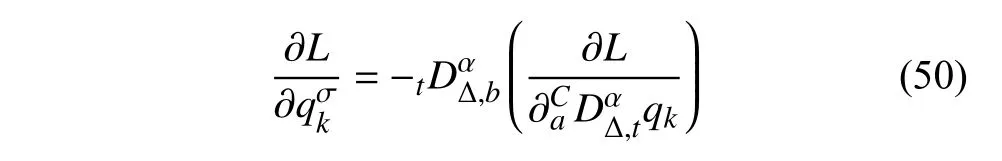
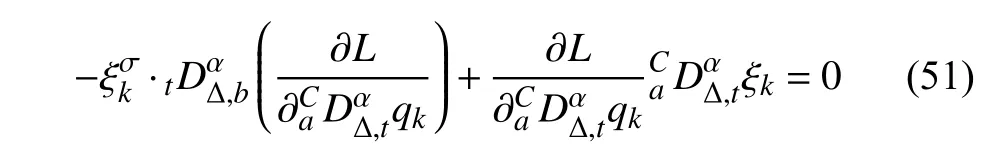
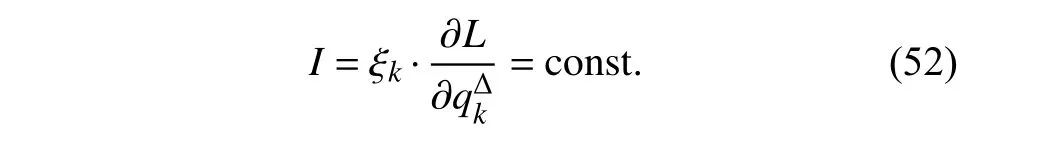
4 一般無限小變換下的分?jǐn)?shù)階時(shí)間尺度Noether 定理
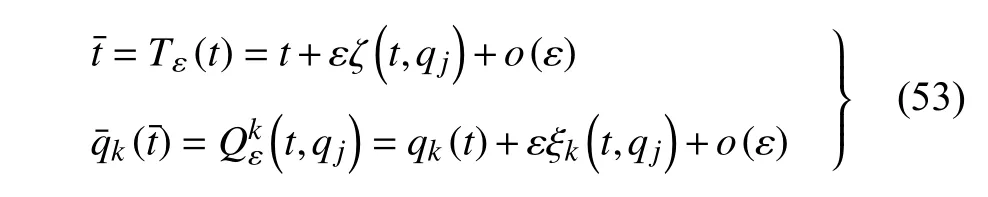
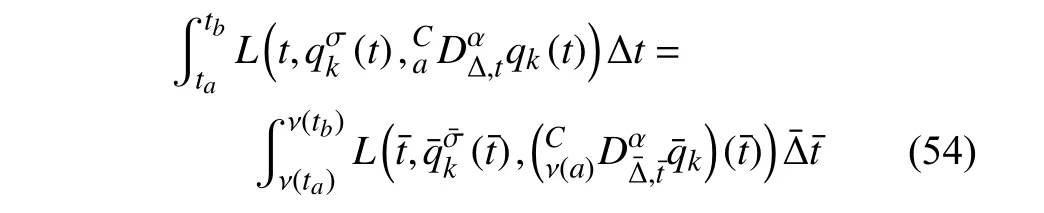
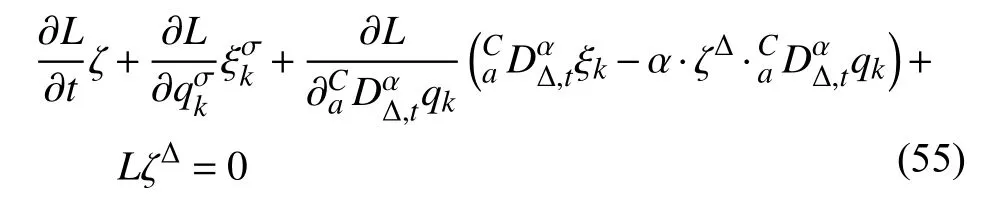
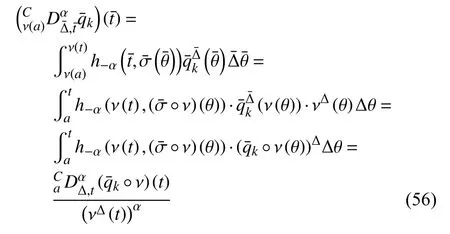
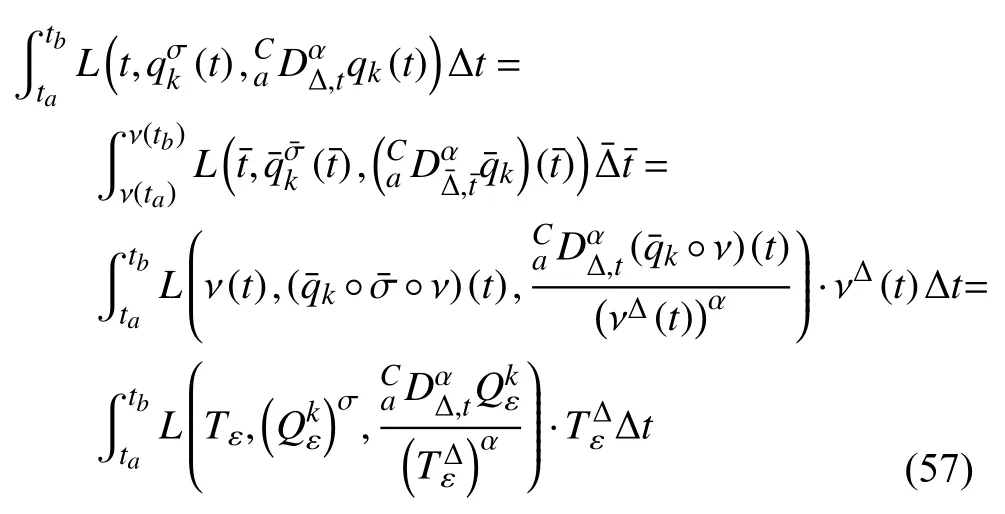
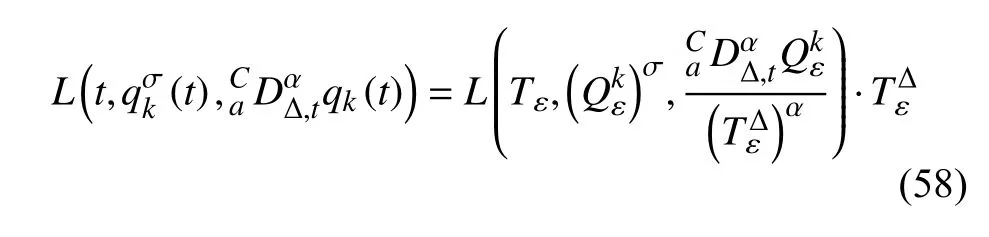
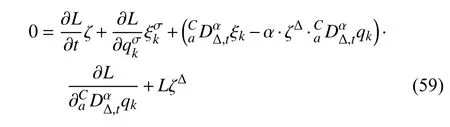
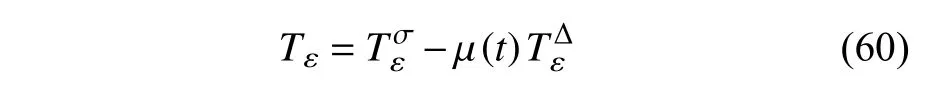
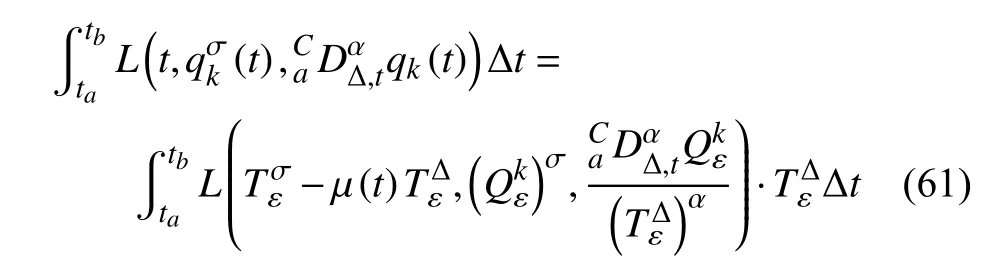
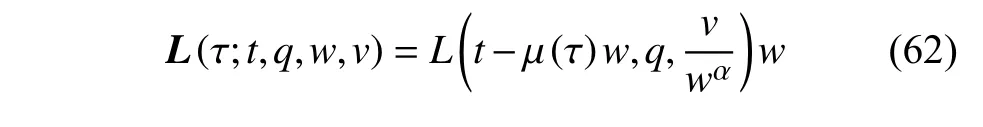
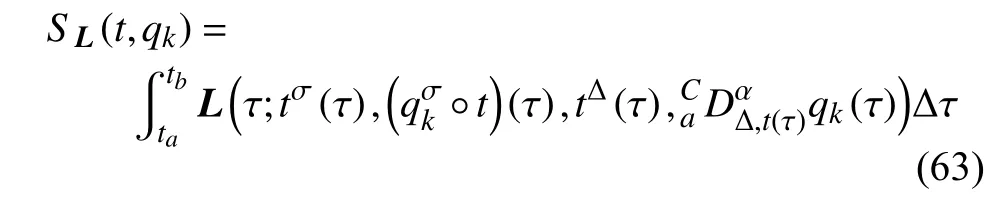
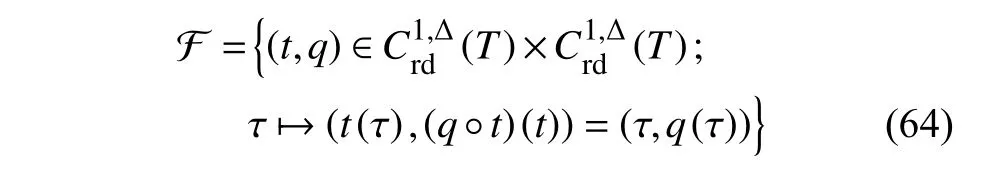

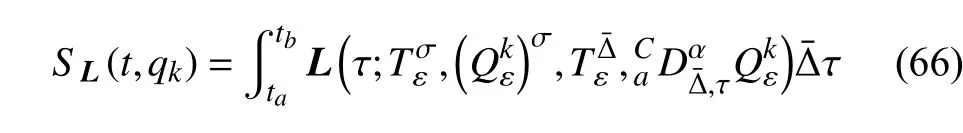
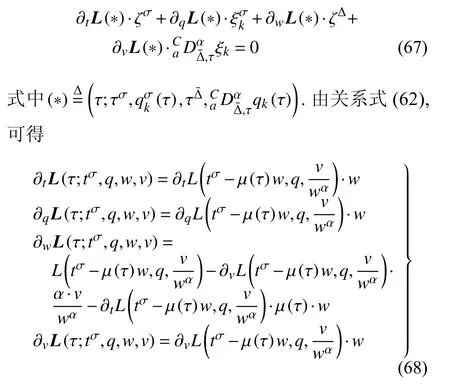
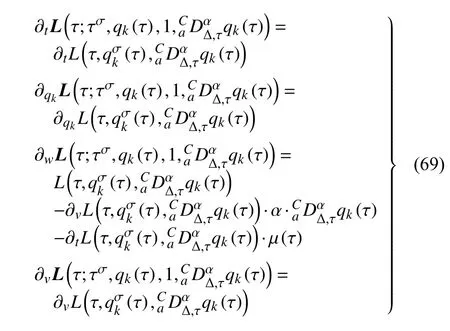
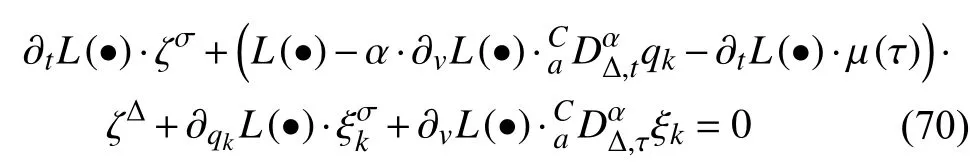
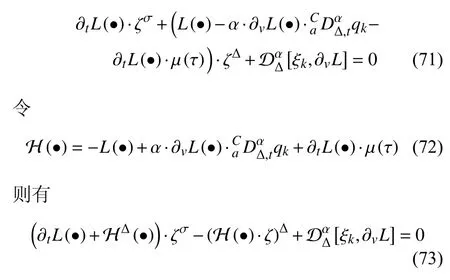
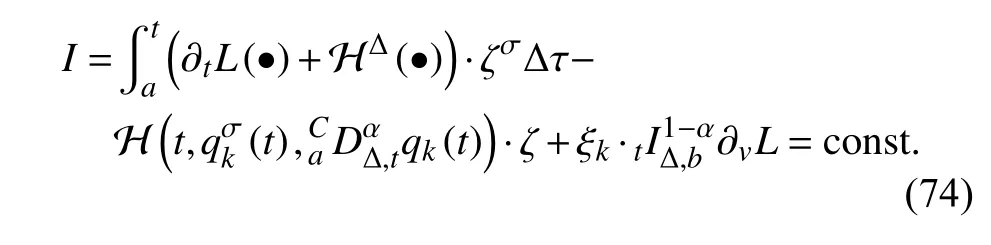
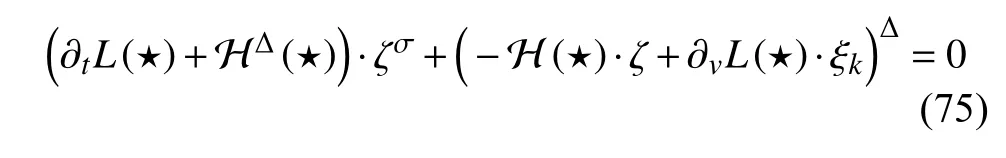
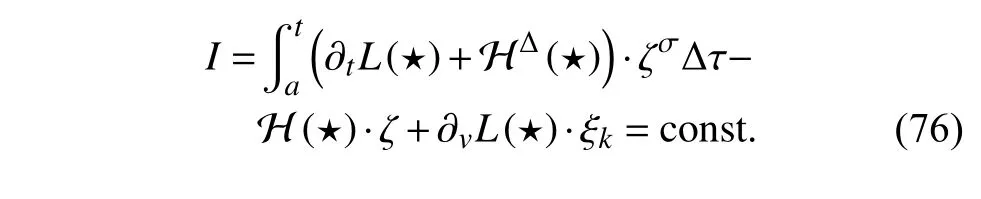
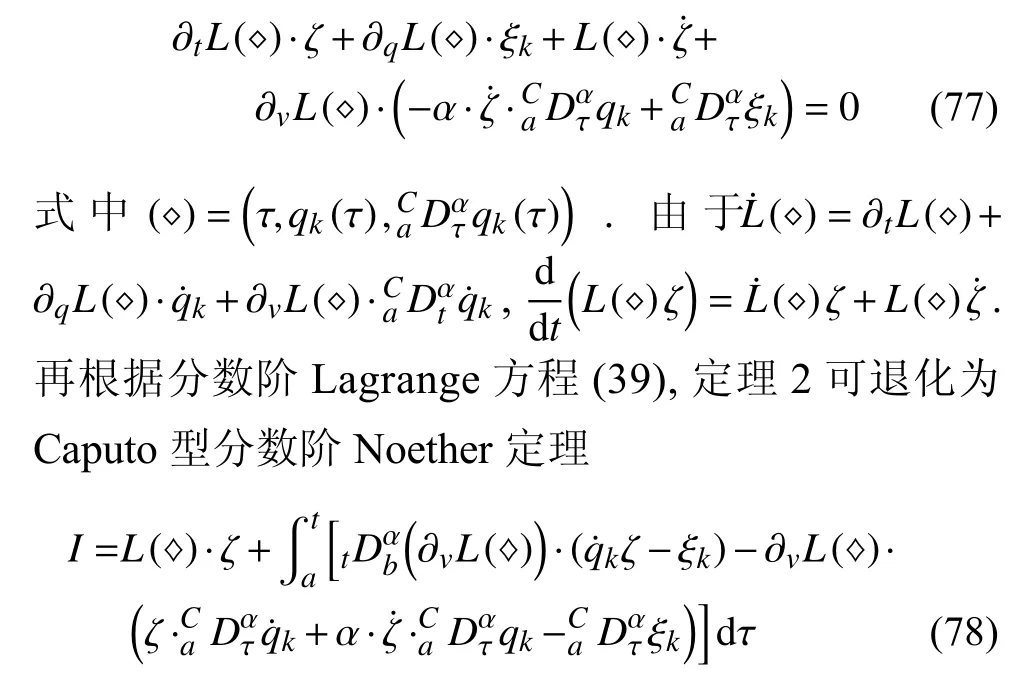
5 算例
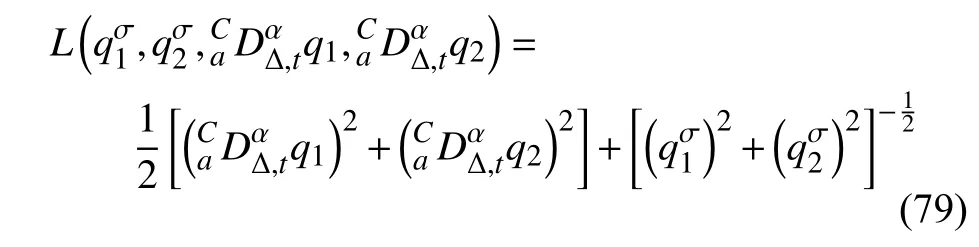
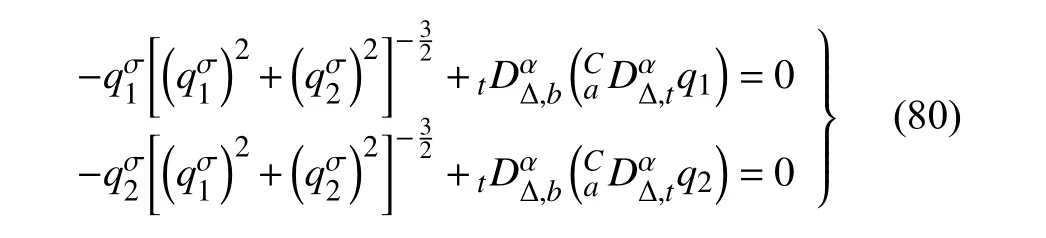
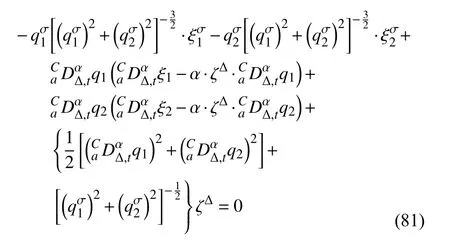
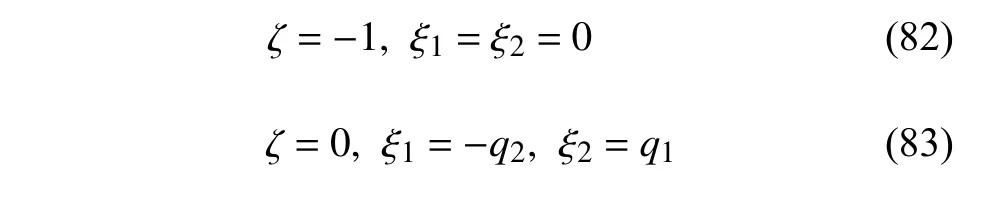
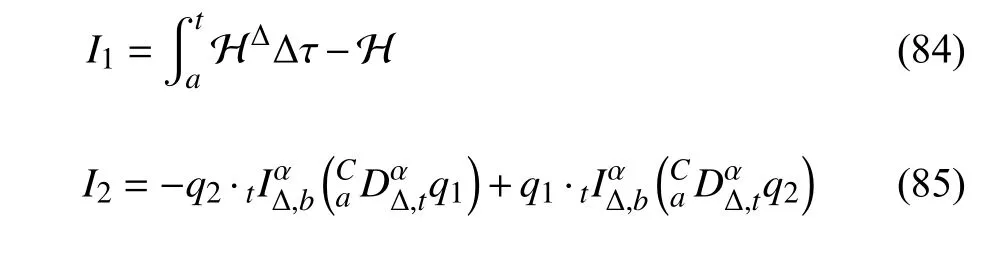
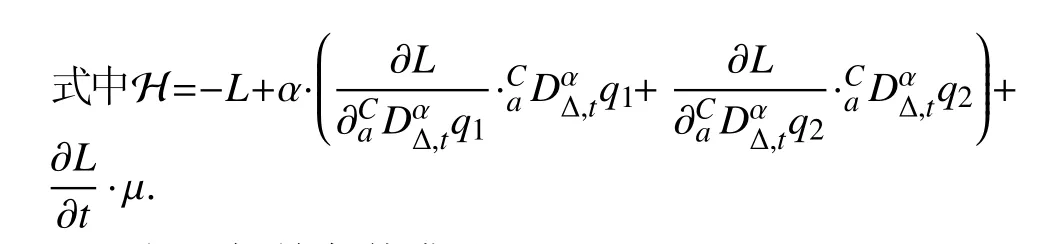
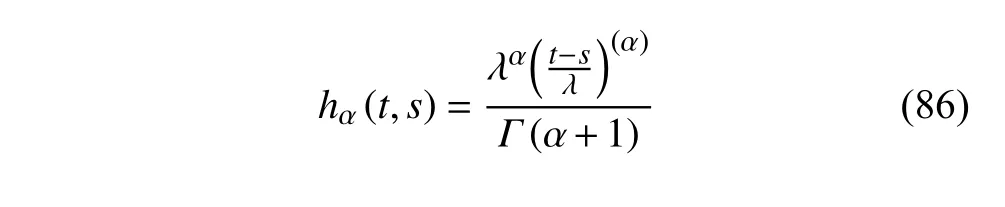
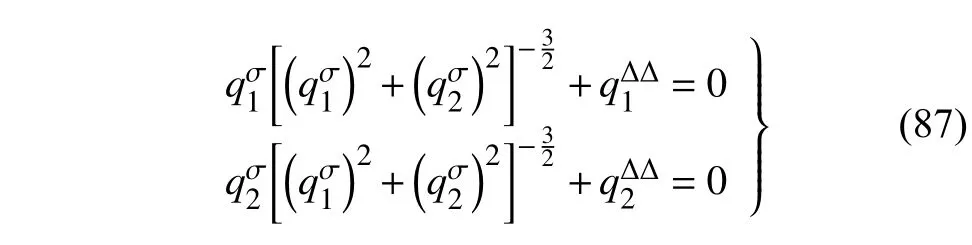
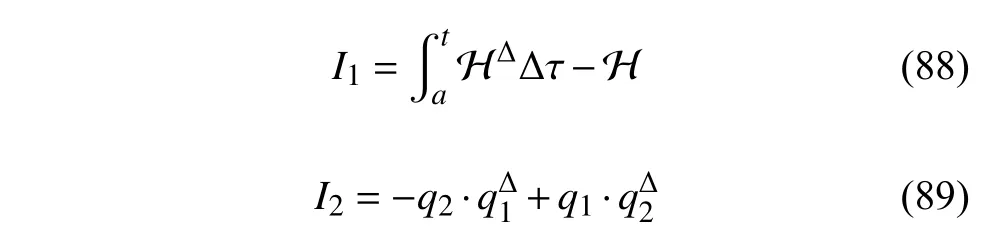
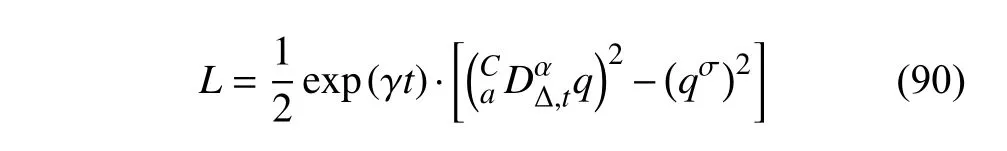
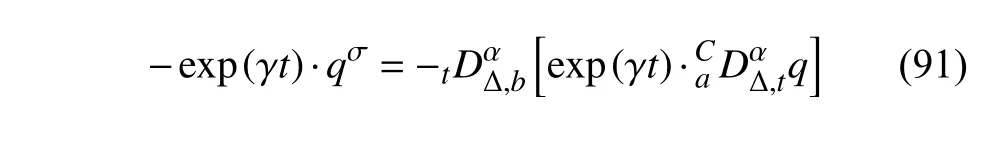
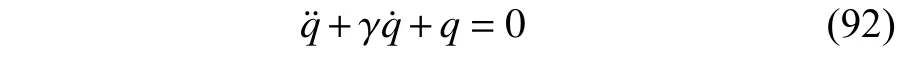
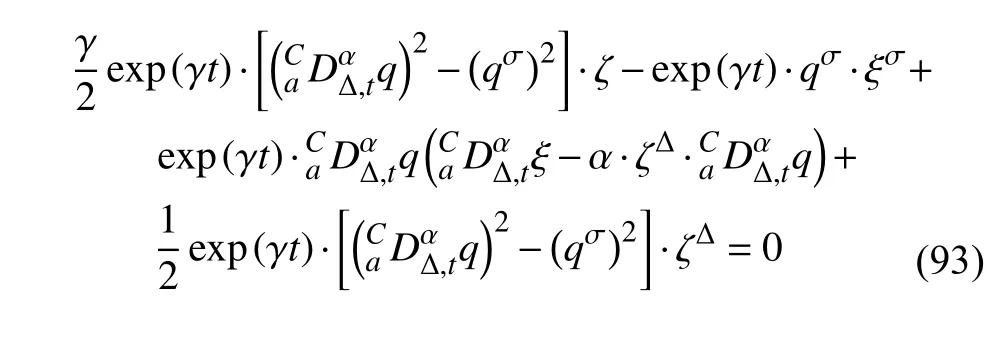
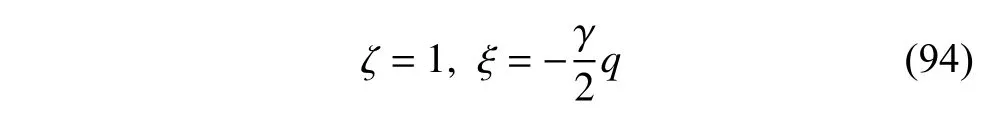
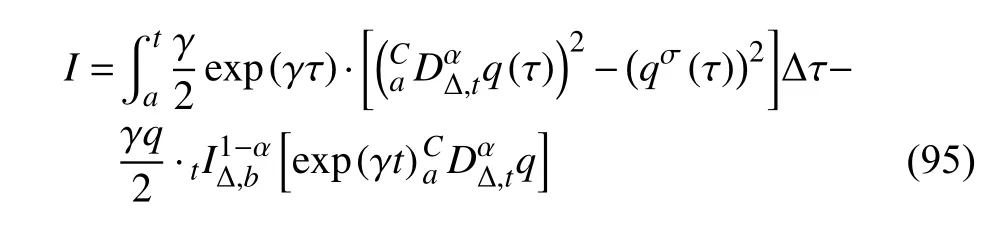
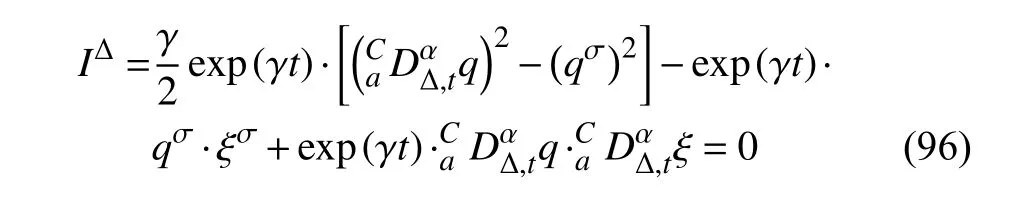
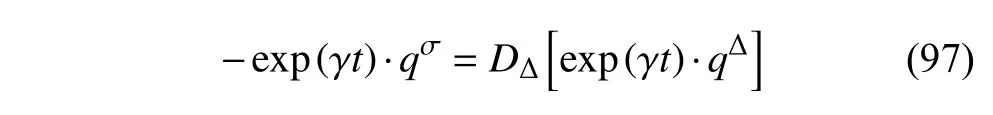
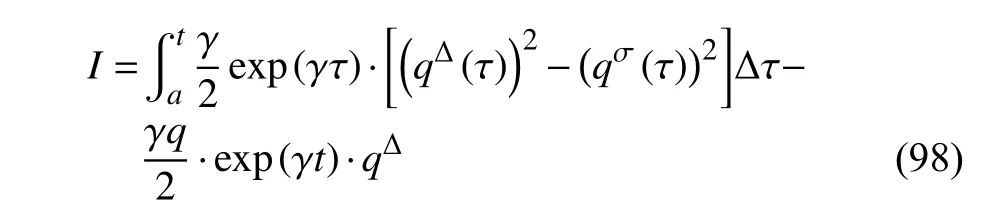
6 結(jié)論

