基于分數階磁流變液阻尼器模型的車輛懸架組合控制1)
張文靜 牛江川,, 申永軍, 溫少芳
* (石家莊鐵道大學機械工程學院,石家莊 050043)
? (石家莊鐵道大學省部共建交通工程結構力學行為與系統安全國家重點實驗室,石家莊 050043)
引言
磁流變液阻尼器是利用磁流變液提供可控阻尼力的裝置,已廣泛應用在車輛懸架[1]、汽車座椅[2]、斜拉索[3]等結構的振動控制中.磁流變液阻尼器通過改變阻尼線圈中的電流強度來改變其磁場強度,能夠快速響應并且輸出阻尼力.描述磁流變液的力學模型主要有Bingham 模型[4-5]、Sigmoid 模型[6]和Bouc-Wen 模型[7]等.其中Bingham 模型由于其結構形式簡單,且物理含義明確而被廣泛應用.劉曉梅等[8-9]為解決整數階Bingham 模型不能描述低速時速度?阻尼力滯回特性的缺陷,提出了磁流變液阻尼器分數階微分形式的Bingham 模型,可以更好地反應其速度?阻尼力的滯回特性.
為了提高車輛的操控性和乘坐舒適性,學者們對磁流變液阻尼器在車輛懸架中的應用進行了深入研究.例如,Sharma[10]研究了含有Bingham 模型的磁流變液阻尼器懸架,通過仿真發現半主動控制比被動控制具有更好的穩定性.Tudon-Martinez 等[11]研究了基于人工神經網絡模型與經典Bingham 模型兩種不同精度水平的阻尼器模型對車輛懸架的影響.Prabakar 等[12]采用Bingham 模型和改進的Bouc-Wen 模型對含磁流變液阻尼器的車輛懸架的半車模型進行了研究,結果表明,具有最優參數的磁流變液阻尼懸架系統比被動懸架性能好一個數量級.李禮夫等[13]通過對汽車磁流變液半主動懸架控制的研究,提出了汽車磁流變液半主動懸架預瞄控制方法,提高了汽車的控制性能.
近年來,分數階微積分理論的應用研究發展非常迅速[14-21].由于分數階微積分可以更好的描述材料的記憶特性[22-23],逐漸成為工程中強有力的建模工具.Vyawahare 和Nataraj[24]建立了核反應堆中子擴散的分數階模型,消除了經典擴散模型的缺陷,能夠更真實的表示核內中子的運動.Jia 和Liu[25]利用分數階微積分理論建立了帶抽頭電感的磁耦合升壓變換器在連續導通模式下的分數階數學模型.陳明等[26]利用少參數分數Zener 模型較好地擬合了鯽魚尾鰭鰭條的松弛特性曲線.蔡偉和陳文[27]從時間和空間分數階兩個方面概述了不同的分數階導數聲波模型.陳丙三等[28]建立了磁流變液測試裝置的分數階模型,且磁流變液的黏彈性可由模型參數獲得.Schiessel 等[29]、Heymans 和Bauwens[30]提出了分數階單元網絡模型和分形流變模型.Niu 等[31]采用分數階磁流變液模型研究了鏜桿系統的半主動振動控制.
在利用磁流變液阻尼器進行車輛懸架振動控制的研究方面,Bingham 模型大都采用的整數階模型,而利用分數階Bingham 模型進行車輛懸架研究的報道還較少.本文采用分數階Bingham 模型來對磁流變液阻尼器進行建模,建立含有磁流變液阻尼器的單自由度1/4 車輛懸架系統動力學模型.利用平均法求解懸架系統在半主動控制下的解析解,并分析控制系統的穩定性.為改善半主動控制對乘坐舒適性的影響,提出一種被動控制與半主動控制相結合的組合控制策略.
1 車輛懸架控制系統模型
非線性車輛懸架不但可以用較低的成本提高乘坐舒適性[32],而且可以提高車輛的平順性[33].建立基于磁流變液阻尼器分數階Bingham 模型的單自由度1/4 車輛懸架系統模型,如圖1 所示.圖中k1和k2分別表示線性剛度和立方剛度,M為簧載質量,c為系統黏性阻尼,x為質量M的位移,x0=Asin(ωt)為路面施加在系統上的位移激勵,A為激勵幅值,ω為激勵頻率.正弦函數可以用來描述起伏路面施加給車輛懸架的激勵,而起伏路面也是車輛測試中較為常見的一種路面[34].
圖中虛線框內表示分數階Bingham 模型磁流變液阻尼器,其最大輸出阻尼力為

其中,fc為分數階Bingham 模型的庫倫阻尼力,p和c1分別為分數階微分項的階次和系數.
采用天棚阻尼半主動控制策略,通過判斷簧載質量的運動速度方向和簧載質量與路面的相對運動速度方向來控制磁流變液阻尼器所提供的阻尼力.系統的運動微分方程為
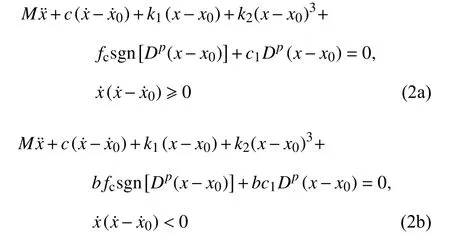
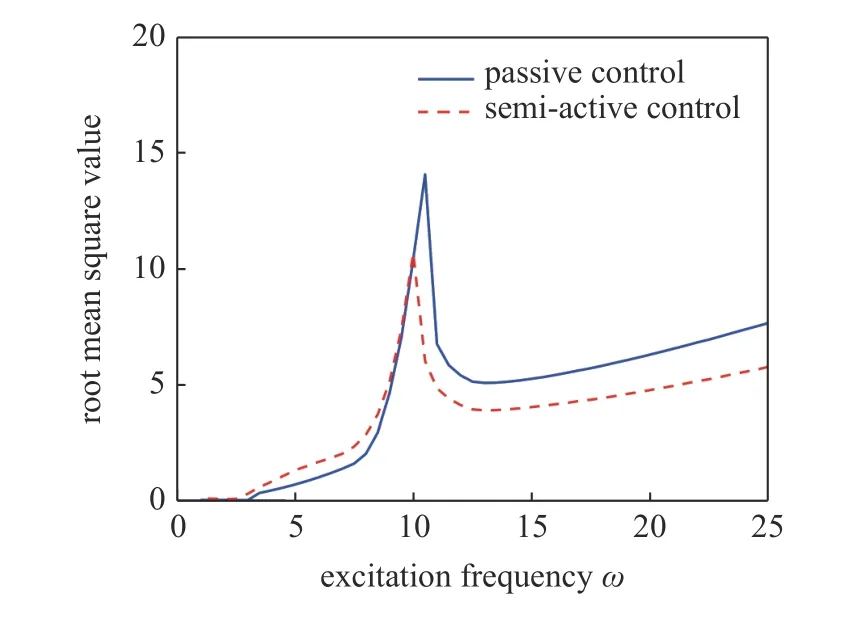
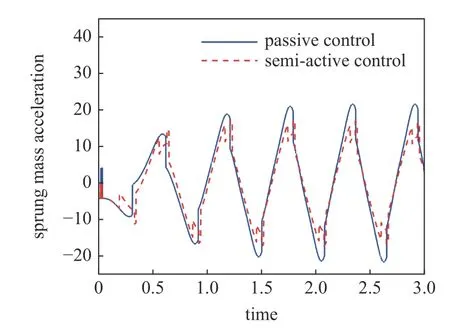
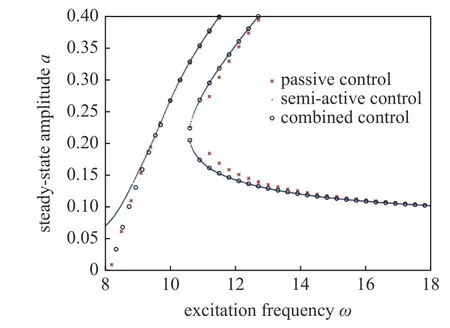
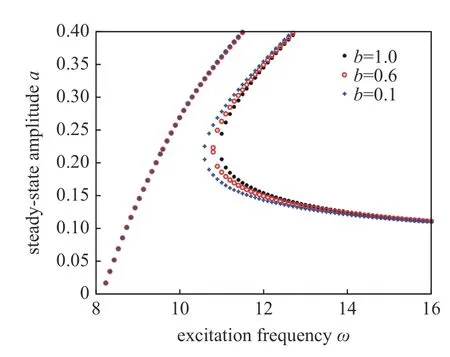
其中,b為隨磁流變液阻尼器的控制電流而變化的參數,即半主動控制參數.當b=1 時,磁流變液阻尼器的輸出阻尼力保持不變,相當于被動控制.分數階階次滿足 0 其中,Γ(z)為Gamma 函數,滿足 Γ(z+1)=Γ(z). 研究系統在半主動控制下的主共振響應,即路面施加給懸架系統的激勵頻率接近系統的固有頻率的響應情況.為了表達激勵頻率與系統固有頻率的接近程度,引入調諧參數 σ,即,其中,為系統的固有頻率. 半主動控制采用天棚阻尼控制策略,即 式(4)中,Fs為磁流變液阻尼器提供的可控阻尼力. 令y=x?x0,式(2)可以改寫為 其中,2εμ=c/M,εη1=k2/M,εfc1=fc/M,εη2=c1/M,F=MAω2,εf=F/M. 設系統(5)在半主動控制下的周期解為 其中,φ=ωt+θ. 天棚阻尼控制策略的控制條件為 當 β>0時,控制力Fs在一個周期內的變化規律為 根據平均法在一個振動周期區間 [0,T] 進行積分,對于周期函數T=2π/ω,可得振幅a與相位 θ 的近似解 式(10)中的第一部分與無控制時相等,即 根據文獻[31],計算穩態響應時分數階微分項可近似表示為 利用式(12) 計算式(10) 的第2 部分,當0<β<時,得到 利用式(12)計算式(10)的第3 部分,可以得到 為簡化上面計算結果,令 將上述計算結果整理為 將系統原參數代入式(17),可以得到 當β≤0時,控制力Fs在一個周期內的變化規律為 利用相同的方法可以得到當 β≤0時的振幅a與相位θ的近似解為 將F=MAω2代入式(22)中并消去,可以得到系統在半主動控制下且 β>0 時的幅頻響應方程和相頻響應方程為 同樣將F=MAω2代入式(24)中并消去,得到系統在 β≤0 時的幅頻響應方程和相頻響應方程為 分析定常解的穩定性,令a=+Δa,θ=+Δθ,當β>0 時,代入式(18)中進行線性化可以得到 進一步得到系統的特征行列式為 將式(27)展開,得到系統的特征方程為 同理,當 β≤0 時,系統的特征行列式為 將式(29)展開,得到系統的特征方程為 經分析可知P恒大于零,根據李雅普諾夫穩定性理論,P>0,Q>0是奇點,漸進穩定的充分條件.因此系統的定常解的穩定性條件為 且當系統有多值解時,中間的一支解為不穩定解. 選擇一組參數驗證解析解的正確性.選擇文獻[8,36-38] 中的參數值,懸架系統的具體參數選擇為:M=240 kg,c=50 N·s/m,k1=15 000 N/m,k2=150 000 N/m3,磁流變液阻尼器的參數選擇為:c1=300 N·s/m,p=0.84,fc=1000 N.路面激勵幅值為A=0.08m.通過Matlab 對系統進行數值計算,利用冪級數法[35]繪制幅頻響應曲線,時間總長設定為150 s,步長設定為0.001 s,并將后30 s 響應的最大值作為穩態響應的峰值.當懸架系統在被動控制即b=1時,其數值計算結果如圖2 所示.根據式(23a)和式(25a)的幅頻響應方程,利用系統的近似解析解將幅頻曲線也繪制在圖2 中.當懸架系統在半主動控制下即b=0.1 時的對比結果如圖3 所示.從圖中可以看出近似解析解和數值解具有較好的一致性,從而驗證了半主動控制解析解計算過程的正確性.從圖2 中數值解可以看出當激勵頻率比較小時,幅頻曲線的幅值響應很小,出現這種現象的原因是當激勵頻率較小時,傳遞到磁流變液阻尼器的外力不足以克服其內部的剪切摩擦力fc,此時的磁流變液阻尼器幾乎沒有運動,即懸架的簧載質量與路面的相對位移很小.由于在車輛懸架系統中存在限位塊,當系統有多解現象時幅值大的上支漸進穩定解在實際應用中并不會出現. 圖2 系統在被動控制下的幅頻響應Fig.2 Amplitude-frequency response of system under passive control 圖3 系統在半主動控制下的幅頻響應Fig.3 Amplitude-frequency response of system under semi-active control 基于單自由度車輛懸架模型研究半主動控制對車輛乘坐舒適性的影響,僅考慮垂直方向的振動控制效果.接下來通過比較懸架系統在半主動控制和被動控制下的簧載質量垂直方向的加速度均方根值來說明半主動控制對車輛乘坐舒適性方面的影響.首先對簧載質量的加速度時間歷程進行頻譜分析,得到功率譜密度函數Ga(f),然后根據下式計算加速度均方根值[39] 其中,W(f) 為頻率加權函數 利用數值計算得到懸架系統在被動控制和半主動控制下,簧載質量的加速度均方根值對比圖,如圖4所示.橫坐標為激勵頻率,縱坐標為簧載質量的加速度均方根值,半主動控制參數b=0.1,振動分析時間選擇120 s,其他參數值保持不變.從圖4 中可以發現懸架在半主動控制下,當路面激勵頻率較小時,簧載質量的加速度均方根值反而比被動控制時還大,說明在車輛懸架的低頻激勵區域,基于磁流變液阻尼器的半主動控制無法起到提高乘坐舒適性的作用.而當路面激勵頻率較大時,半主動控制在提高乘坐舒適性方面起到了很好的作用. 圖4 加速度均方根值Fig.4 RMS of acceleration 當激勵頻率在主共振頻率附近 ω=11 rad/s 時,半主動控制參數為b=0.1 和被動控制時的簧載質量的加速度時間歷程對比圖如圖5 所示,圖中截取了前3 s 的加速度時間歷程,其他參數值與第4 節相同.從圖5 中可以看出,在該頻率的激勵下半主動控制能有效降低簧載質量的加速度峰值,從而提高了車輛的乘坐舒適性. 圖5 簧載質量的加速度時間歷程Fig.5 Acceleration time history of sprung mass 為了解決半主動控制會在低頻激勵區域降低乘坐舒適性的問題,采用一種組合控制策略,即當路面的外激勵頻率小于切換頻率時,懸架系統采用被動控制策略進行振動控制;而當外激勵頻率值大于切換頻率時,懸架采用半主動控制策略進行振動控制. 當b=1 時,即被動控制的幅頻響應方程為 根據式(34)以及半主動控制參數為b=0.1 時的幅頻響應方程,可以得到兩條幅頻響應曲線在固有頻率附近的交點對應的頻率為:ωi=9.54 rad/s.將該幅頻響應曲線交點對應的頻率作為組合控制的切換頻率.利用數值解和解析解分別繪制懸架系統在組合控制下的幅頻響應曲線,如圖6 所示.從圖中可以看出數值解與解析解具有較好的一致性. 圖6 系統在組合控制下的幅頻響應Fig.6 Amplitude-frequence response curves of system under combined control 為了驗證組合控制的振動效果,利用近似解析解分別得到懸架系統在被動控制、半主動控制以及組合控制下的幅頻響應曲線,如圖7 所示.其中,半主動控制參數為b=0.1.當系統有多解時,僅考慮最下面一支穩定解的結果.從圖7 中可以看出,懸架系統在組合控制下的主共振振幅最小.而當激勵頻率增大到一定程度,半主動控制將失去對振幅的抑制作用,效果將又和被動控制一致. 圖7 不同控制策略下的幅頻響應Fig.7 Amplitude-frequence response curves under different control strategies 為了研究半主動控制參數b對懸架系統在組合控制下的影響,分別選取b=0.1,b=0.6,b=1 時,利用近似解析解得到系統的幅頻響應曲線,如圖8 所示.同樣僅考慮最下面一支穩定解的結果,從圖8 中可以看出,半主動控制參數b值越小,系統的主共振幅值越小.在頻率 ω=11 rad/s時,當b=0.1 時共振幅值為0.169 8 m;當b=1 時,即懸架系統在被動控制作用下時,共振幅值為0.205 1 m.懸架系統在組合控制作用下的共振峰值比被動控制的共振幅值減小了約0.035 3 m. 圖8 b 變化時對組合控制的影響Fig.8 Effect of combined control with different b 本文將磁流變液阻尼器的分數階Bingham 模型應用到單自由度1/4 車輛懸架系統的動力學分析中,研究了懸架系統的振動控制.通過平均法研究了系統在半主動控制下的主共振響應,得到了系統的近似解析解,并通過數值解驗證了近似解析解的正確性.通過比較懸架系統在半主動控制和被動控制作用下的簧載質量垂直方向的加速度均方根值,說明了半主動控制在路面激勵頻率小于固有頻率附近的切換頻率時反而會降低車輛的乘坐舒適性,繼而提出了一種被動控制與半主動控制相結合的組合控制策略,并利用系統在被動控制和半主動控制下的兩條幅頻響應曲線在固有頻率附近的交點對應的頻率作為切換頻率.分析結果表明,該組合控制策略不但可以提高乘坐舒適性,還可以有效抑制懸架系統的主共振振動幅值.為分數階磁流變液阻尼器模型在車輛懸架中的應用提供了參考.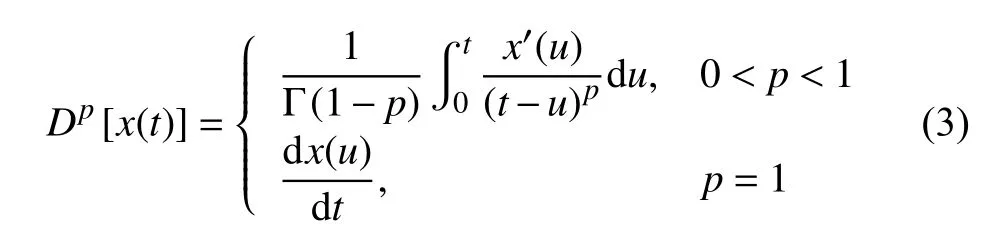
2 半主動控制下的近似解析解
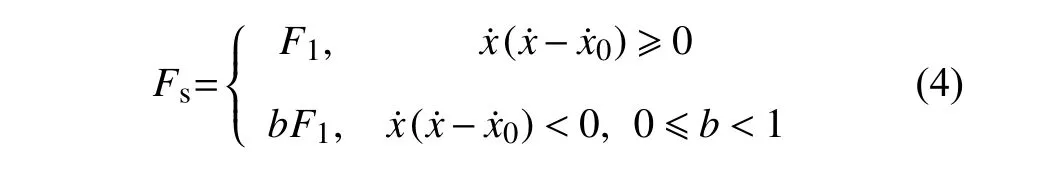

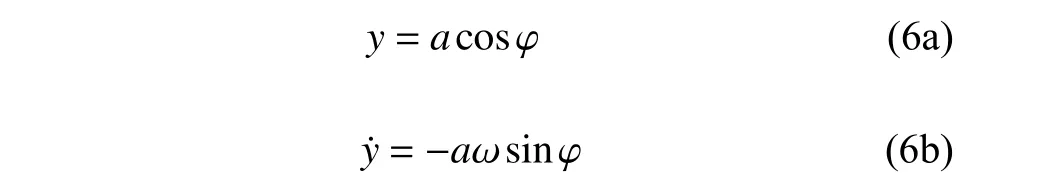
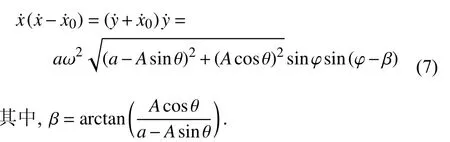
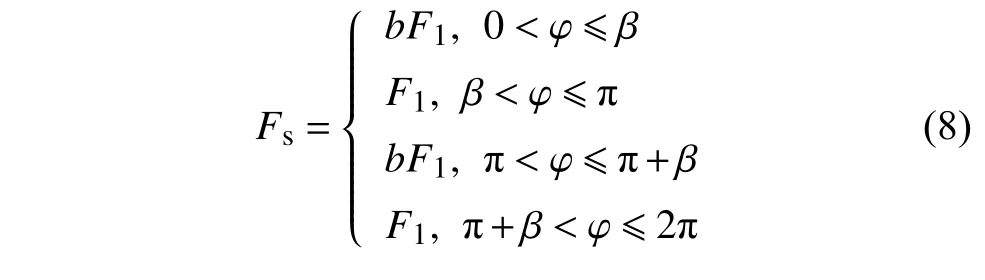

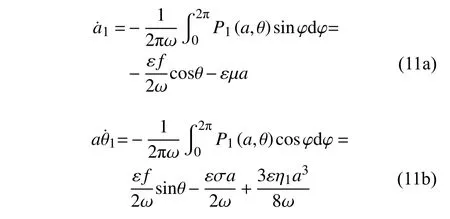



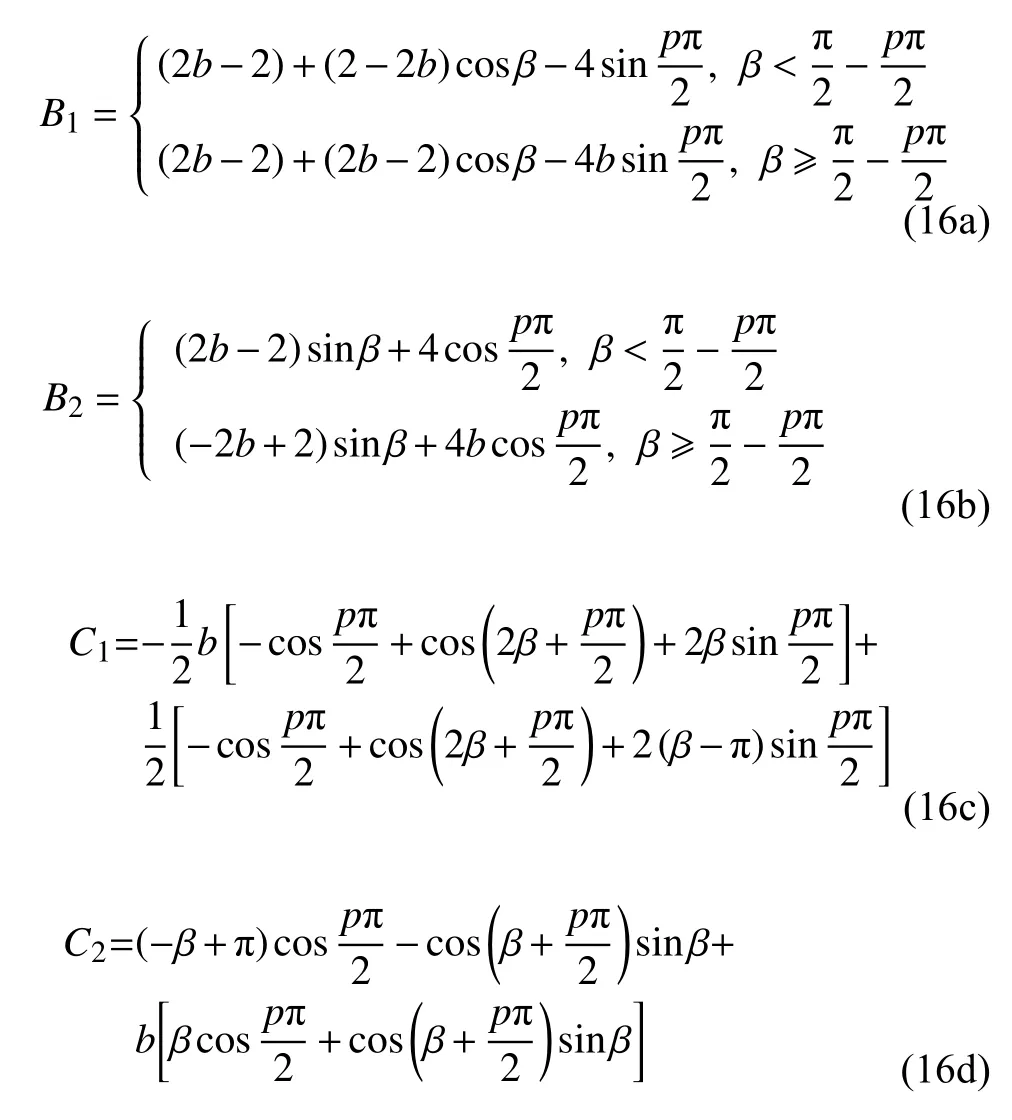
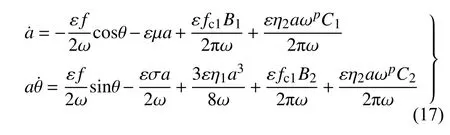
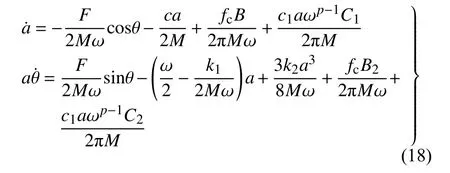


3 定常解及其穩定性分析
3.1 半主動控制的定常解
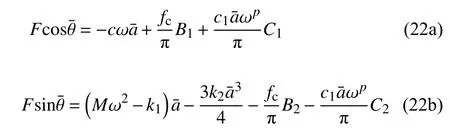
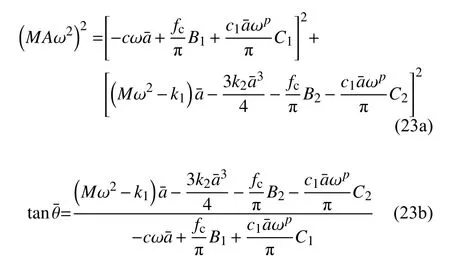
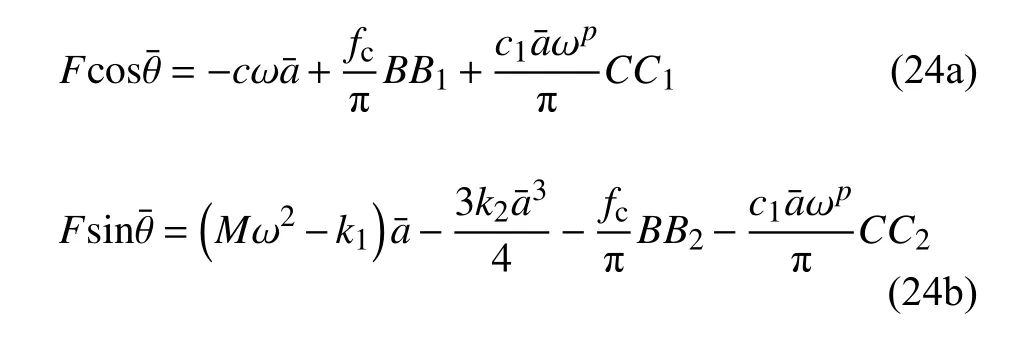

3.2 半主動控制下的穩定性分析

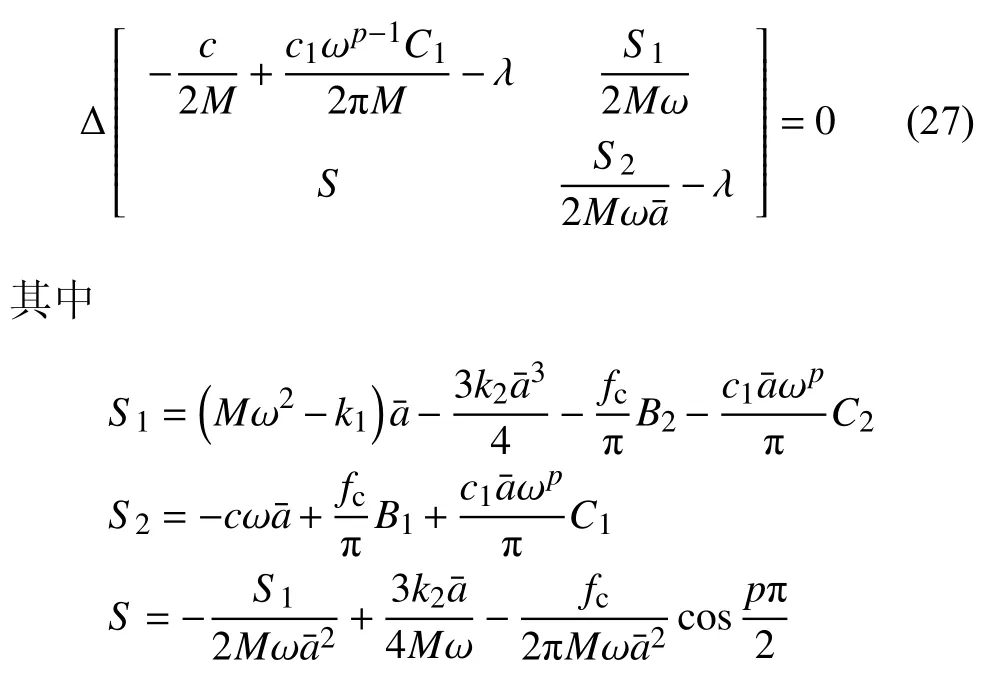


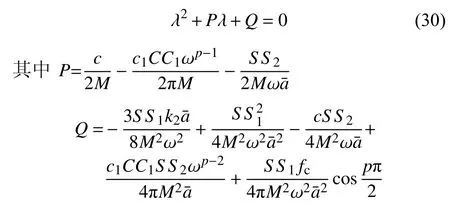
4 數值解驗證


5 半主動控制對乘坐舒適性的影響
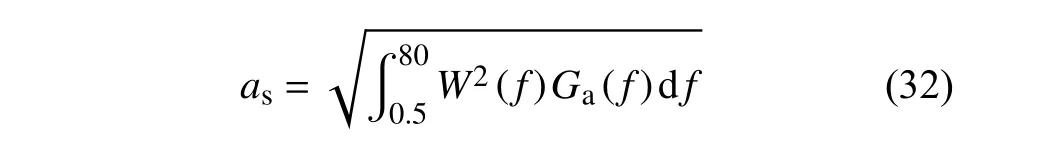
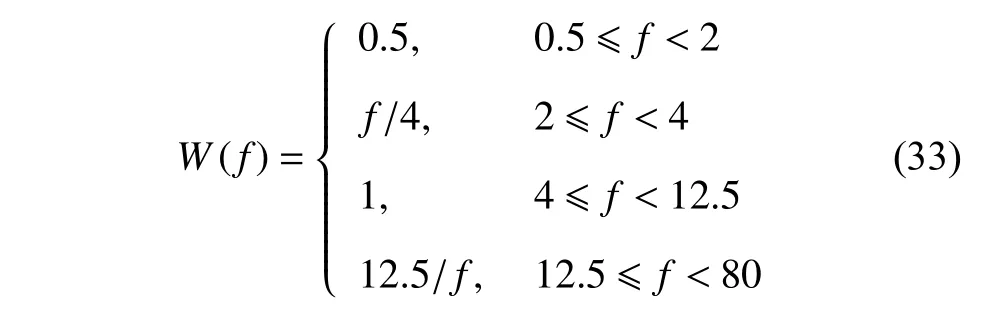


6 組合控制的振動控制效果分析
7 結論

