巧用極化恒等式破解向量數量積問題*
2021-11-10 03:01:00安徽省合肥市第一中學230601谷留明
中學數學研究(江西) 2021年10期
關鍵詞:背景
安徽省合肥市第一中學 (230601) 谷留明
平面向量是高中數學較為重要的內容,其中數量積內涵豐富,是連接各知識點的核心概念,也是平面向量和其他知識相融合的重要渠道.在高考和競賽中,經常涉及到數量積的求值或最值問題,在平時的教與學中,師生比較關注定義法、坐標法、基底法,有時也用投影法.但有些數量積問題,若用前面這些方法,就不太行得通或者不夠簡潔,而如果能夠巧用極化恒等式,問題往往能夠迎刃而解.
一 公式介紹

圖1
二 公式妙用
1.以三角形或多邊形為背景

解析:如果采取將不等式兩邊平方,運算量非常大.其實由向量的減法及數乘運算的幾何意義,根據已知不等式,可得點P到直線AB的距離為3,所以△PAB由P出發的中線最短為3,而且AB邊長為定值10,所以具備用極化恒等式的典型條件.

圖2


圖3

2.以圓為背景
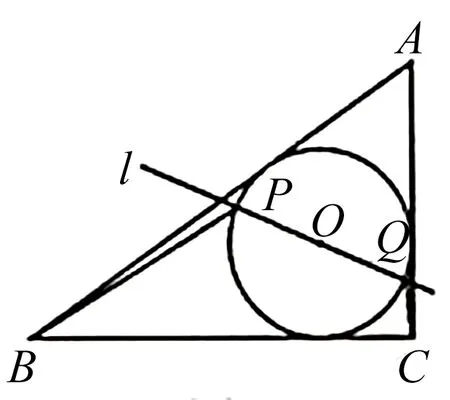
圖4

解析:此題用坐標法是可以的,但運算過程不夠簡潔,如果要用極化恒等式,初看起來好像不具備相應特征.如果能動中取靜,就會注意到圓O和Rt△ABC是固定的,點P,Q在運動中恒以定點O為中點.


3.以圓錐曲線為背景

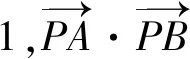
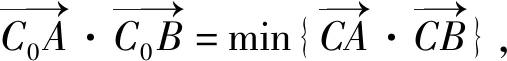
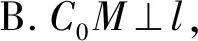
4.以立體幾何為背景

圖6
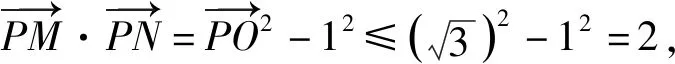

猜你喜歡
教學考試(高考化學)(2022年5期)2022-11-19 14:15:16
汽車工程師(2021年12期)2022-01-17 02:29:54
當代陜西(2020年14期)2021-01-08 09:30:42
奧秘(創新大賽)(2020年7期)2020-07-27 08:26:32
活力(2019年21期)2019-04-01 12:18:06
中國自行車(2018年10期)2018-11-30 02:09:04
貴州師范學院學報(2016年4期)2016-12-01 03:54:07
紡織服裝流行趨勢展望(2016年1期)2016-05-04 03:45:20
語文知識(2015年11期)2015-02-28 22:01:59
中國衛生(2014年10期)2014-11-12 13:10:16

