一道三元分式函數值域問題的反思及推廣
2021-11-10 06:17:46廣州大學附屬中學510006朱驚濤
中學數學研究(江西) 2021年10期
關鍵詞:數學
廣州大學附屬中學 (510006) 朱驚濤
廣州大學數學與信息科學學院 (510006) 蔡 飄
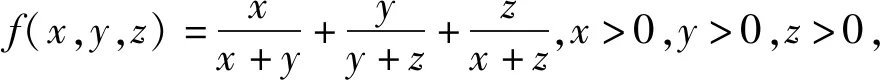
該問題相當于求函數f(x,y,z)的值域,其標準答案如下:
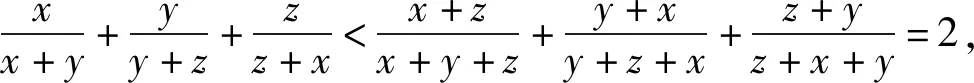
反思該答案,比較難以理解的是求極限過程中為何要令z=1,筆者經過分析發現,其實不一定要令z=1,令z等于任何一個常數都是可以的,其思想方法就是固定z,然后分別讓x、y趨向兩邊,從而得到f(x,y,z)取值的一種極限狀態.考慮到用降元法解決多元問題的數學思想,筆者給出該問題的另一種解法:
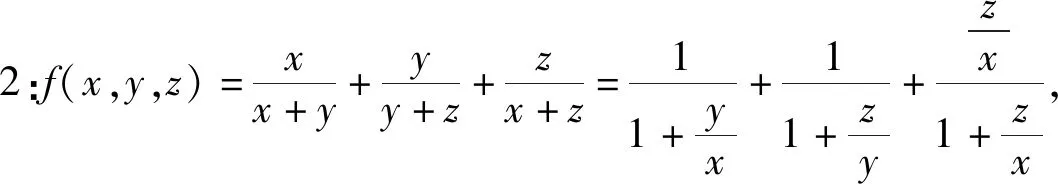
結論1 令min{a,b,c}表示a,b,c中的最小值,max{a+b,a+c,b+c}表示a+b,a+c,b+c中的最大值,則函數f(x,y,z)的值域為(min{a,b,c},max{a+b,a+c,b+c}).
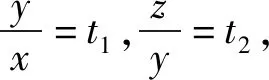
①當t1→0,t2→0時,g(t1,t2)→a+b;
②當t1→+∞,t2→+∞時,g(t1,t2)→c;
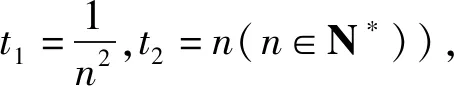

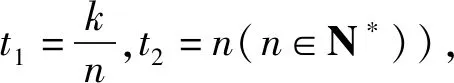
⑥當t1→+∞,t2→0時,可令t1t2→0,此時g(t1,t2)→b;
⑦當t1→+∞,t2→0時,可令t1t2→+∞,此時g(t1,t2)→b+c;
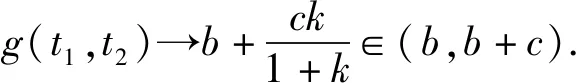
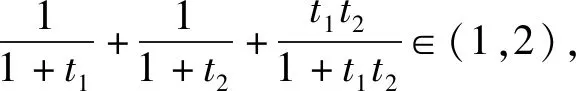


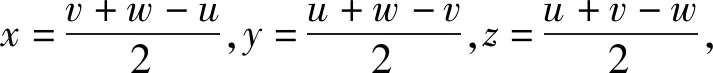
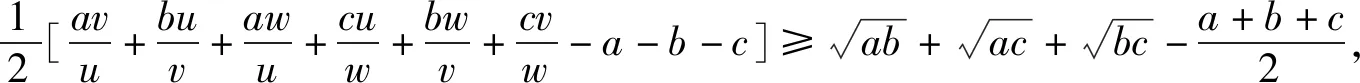
該結論還可以推廣到n元的情形,即:
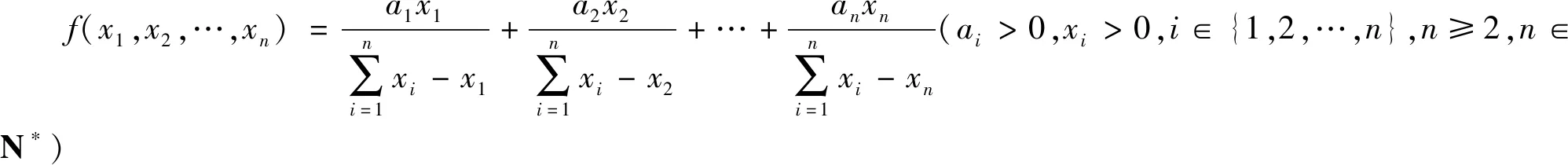
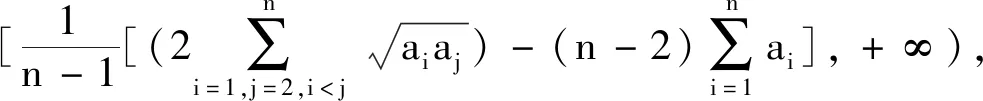
猜你喜歡
中等數學(2021年4期)2021-12-04 13:57:52
中等數學(2021年7期)2021-12-03 04:01:41
中等數學(2021年1期)2021-12-02 03:08:08
中等數學(2021年3期)2021-12-02 00:28:14
中等數學(2020年11期)2020-12-18 01:23:21
學苑創造·A版(2019年5期)2019-06-17 01:14:21
新民周刊(2016年15期)2016-04-19 18:12:04
新民周刊(2016年15期)2016-04-19 15:47:52
傳奇故事(破繭成蝶)(2015年7期)2015-02-28 09:29:27
漫畫月刊·炫版(2014年3期)2014-05-27 04:17:21

