基于GeoGebra平臺下對一道橢圓試題的探究與推廣*

廣東省中山市小欖中學 (528415) 李 琨

廣東省中山市濠頭中學 (528437) 閆 偉

圓錐曲線與直線的位置關系一直是高考的熱點和難點，在很多圓錐曲線題目中都是探求一些特殊結論，這些結論看似特殊，實則都具普遍性，而且往往具有豐富的命題背景和深厚的內涵，研究此類試題不僅能夠更好的把握解析幾何的本質，還能透過試題挖掘隱含的命題規律，更能將其拓展到一般情況，從而提升學生數學思維,發展數學核心素養.下面筆者以復習備考中的一道橢圓試題的探究為例進行說明.

1試題呈現與分析

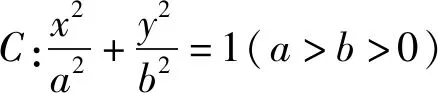
試題分析：本題主要考查橢圓的標準方程及其幾何性質、直線與橢圓的位置關系、韋達定理以及橢圓中的動點軌跡和定值問題等內容，重點考查學生的推理論證能力、運算求解能力以及綜合運用所學知識分析問題和解決問題的能力.試題結構清晰，問題設置層次分明，內涵豐富；試題第(2)問強化探究運算思路，選擇運算方法，彰顯數學運算和邏輯推理等核心素養，較好地檢測了學生的學習潛能和數學素養.

2 解法探究

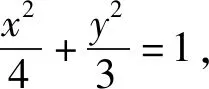
評注：設線法是比較自然的解法，設直線方程與橢圓聯立并借助韋達定理進行參變量的代換，進而表示動點坐標，然后確定兩條直線方程利用交軌法定Q點軌跡為一個圓，進而得到目標點H即為該圓的圓心.

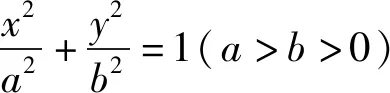
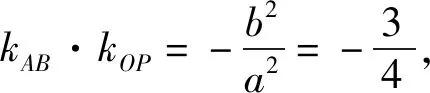
評注：解法2巧妙借助中點弦的斜率性質，從直線斜率角度來確定直線OP與直線EQ的位置關系得到Q點軌跡進而鎖定目標點H，不僅體現了問題的本質，同時極大簡化了推理運算過程，實現高效解題，要求學生對重要結論的積累和靈活運用.

3 基于GeoGebra的探究及反思

通過以上的分析和解答，直線OP與直線EQ的交點Q在定圓上，從而所求點H即是定圓的圓心那么該結果是偶然還是必然呢？兩直線交點的軌跡和題目中橢圓的參數OP,EQ以及直線OP,EQ的位置有關系嗎？如果將參數OP,EQ以及直線OP,EQ一般化，又會得到什么結果呢？由于涉及到的運算和直線OP,EQ的方程較為復雜，探究兩直線交點的軌跡有一定的難度，因此筆者借助于GeoGebra平臺進行探究，通過實驗演示來找到與上述參數相關的定曲線方程，同時為后面的代數證明提供更加直觀的思路支持.

實驗1 (1)在GeoGebra繪圖中先設置兩個“滑動條”控制變量a,b，輸入x^2/a^2+y^2/b^2=1得到一個橢圓C；(2)輸入框中輸入焦點[C]，得到橢圓的右焦點F，過點F作直線與橢圓交于A、B兩點，與y軸于點E；(3)利用中點工具作出A、B中點P并作直線OP；(4)利用工具欄作出過點E且垂直OP的直線交OP于點Q，點擊跟蹤點Q軌跡；(5)拖動直線AB觀察點Q的軌跡(如圖1).

實驗2 (1)在GeoGebra繪圖中先設置兩個“滑動條”控制變量a,b，輸入x^2/a^2+y^2/b^2=1得到一個橢圓C；(2)再通過“滑動條”設置一個變量t，作出點F(t,0)并過點y作直線與橢圓交于A、B兩點，與y軸于點E；(3)利用中點工具作出A、B中點P并作直線OP；(4)利用工具欄作出過點E且垂直OP的直線交OP于點Q，點擊跟蹤點Q軌跡；(5)拖動直線AB觀察點Q的軌跡(如圖2).或者改變橢圓參數a,b及參數t繼續重復上述操作，點Q的軌跡仍然是一條定曲線.

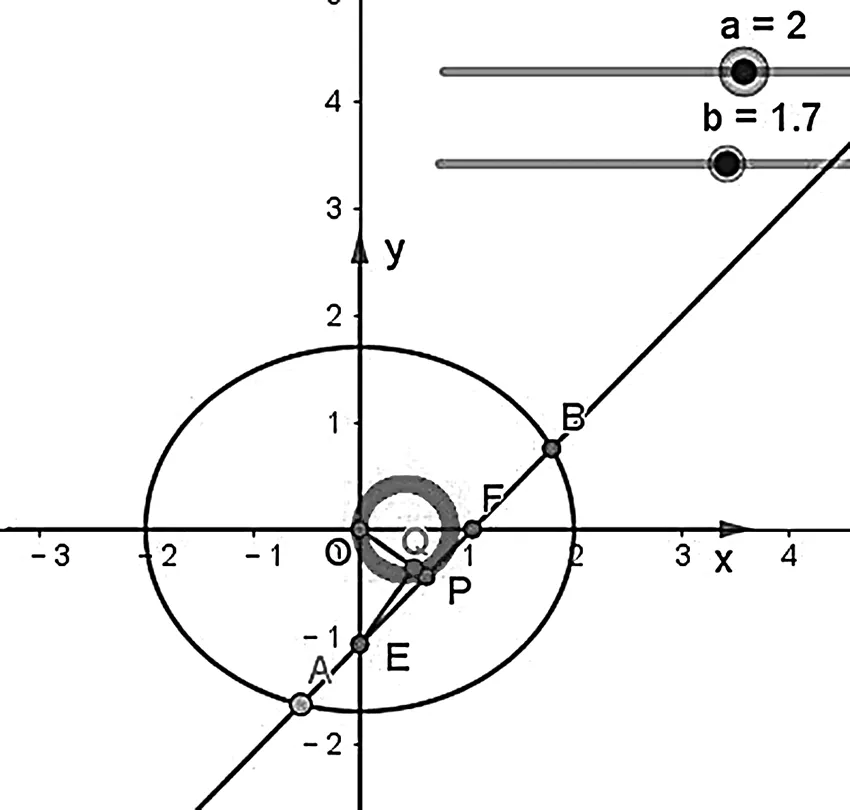
圖1

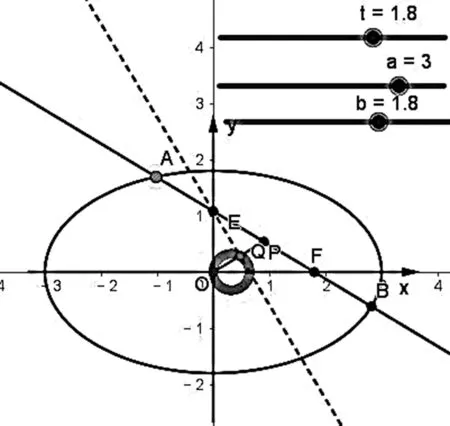
圖2

根據以上實驗的探究結果，師生可以直觀認識到直線OP,EQ的交點Q恒在與參數a,b，t有關的定曲線上，于是我們可以將試題結論推廣到一般情形：

4 推廣結論 揭示本質

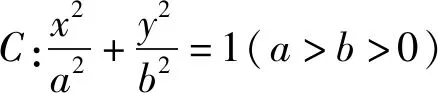
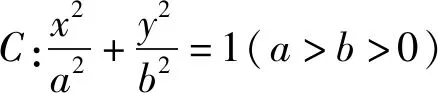
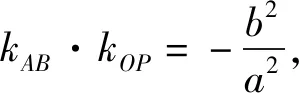
顯然當t=c時，結論1是結論2的特例；若將橢圓換成雙曲線，利用GeoGebra軟件繼續探究，經同樣的實驗操作，發現點Q的軌跡仍在定曲線上(如圖3)，從而有如下結論：

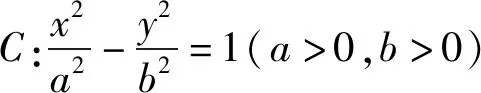
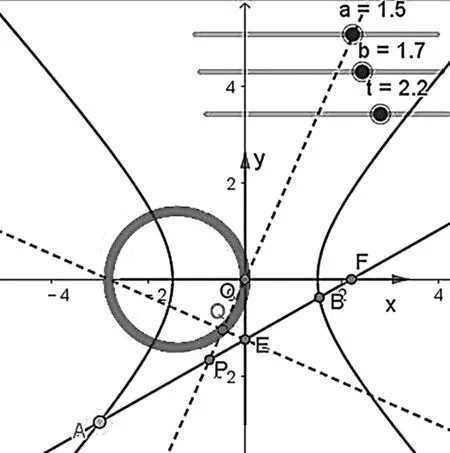
圖3

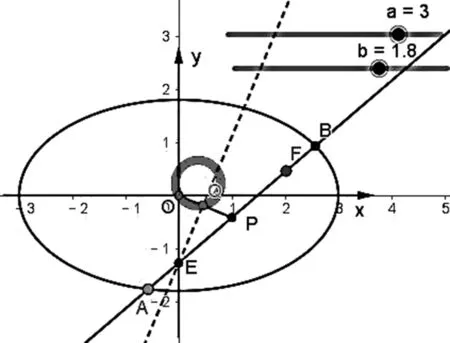
圖4

由于橢圓和雙曲線都是有心二次曲線，當點F是曲線內異于原點的任意一點時，按照上述實驗2的操作步驟，拖動直線AB發現點Q的軌跡仍是一個定圓(如圖4).從而進一步可以將上述結論統一為：

結論4 過有心二次曲線C內異于原點的一點F作一條斜率不為零的直線交曲線C于A、B兩點，交y軸于點E，P為弦AB中點，過點E作直線OP的垂線交OP于點Q，則點Q的軌跡是一個定圓.

結論3和結論4的證明過程與結論2相仿，此處不再贅述，留給有興趣的讀者.

5 探后反思 引領教學

《普通高中數學課程標準(2017)》明確指出，“提升信息技術的使用能力，通過信息技術與課程的深度融合以及課程資源開發的多樣化實現”.這就需要合理運用信息技術，以此提高數學教學的有效性.在本文的探究中，運用GeoGebra技術制作橢圓模型，再通過控制變量不斷改變動直線和方程參數來演示圖形變化過程，讓學生觀察所求動點的軌跡的運動情況，進而將實驗結果拓展到有心二次曲線的統一結論，不僅為學生理解試題本質創設教學情境，而且為學生探索試題規律啟發思維，為學生解決數學問題提供直觀的思路支撐，而且實現了數學對象的多元表征(數字、表達式、圖形等)，使得抽象的數學知識變得形象直觀，有助于培養學生直觀想象等核心素養[1].