巧變形 妙構造*——利用導數(shù)證明不等式幾種構造函數(shù)策略

福建省莆田第二中學 (351131) 卓曉萍

福建教育學院基礎教育研究院數(shù)學教育研究所 (350025) 蔡海濤

縱觀近幾年的高考題，利用導數(shù)證明不等式問題多次出現(xiàn)，充分考查了數(shù)學抽象、數(shù)學建模、數(shù)學運算、邏輯推理素養(yǎng)，突出理性思維，彰顯選拔功能.在解決這類問題的過程中，欲證不等式f(x)>g(x)，常需要構造函數(shù)求導、判斷單調(diào)性、求最值，學生解題的難點在于如何構造函數(shù).本文筆者以一道2021年廈門市高三質(zhì)檢題為例，歸納整理幾種構造函數(shù)策略，與各位同仁交流．

一、題目呈現(xiàn)

已知函數(shù)f(x)=2ax-ln(x+1)+1，a∈R.

(1)討論f(x)的單調(diào)性；(2)當x>0，0f(x).

二、解法賞析

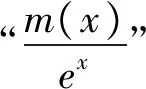
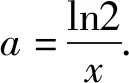
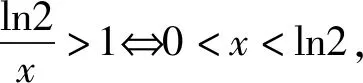
評析：本解題策略是更換主元，構造函數(shù)，利用新函數(shù)最值證明不等式.由于不等式結構中含有雙元a,x，F(xiàn)(a,x)=exa-2xa+ln(x+1)-1，可以看做關于變量“a”的函數(shù)，也可以看做關于變量“x”的函數(shù).若把函數(shù)F(a,x)中主元定為a，得F(a)=exa-2xa+ln(x+1)-1，F(xiàn)(a)是含有“ea，a”兩類結構的超越函數(shù)，若把函數(shù)F(a,x)中主元定為x，F(xiàn)(x)=exa-2xa+ln(x+1)-1，h(x)是含有“ex，x，lnx”三類結構的超越函數(shù)，相比之下F(a)結構更為簡單易分析.

解法4：(巧妙放縮，構造新函數(shù))由02ax-ln(ax+1)+1，即eax-ax>ax-ln(ax+1)+1=eln(ax+1)-ln(ax+1)+1，令h(x)=ex-x，只需證h(eax)>h(ln(ax+1))，有h′(x)=ex-1>0，得h(x)在(0,+∞)上單調(diào)遞增，只需證eax>ln(ax+1)，利用不等式ex>x+1(x>0)，x>ln(x+1)(x>0)，得eax>ax+1>ln(ax+1)+1.

評析：本解題策略是利用已知a的范圍02ax-ln(ax+1)+1，不等式中出現(xiàn)“et,t,lnt”的結構，觀察“et-t,t-lnt”的結構一致，構造函數(shù)h(x)=ex-x，把問題轉(zhuǎn)化為h(eax)>h(ln(ax+1))，再結合h(x)單調(diào)性，進一步簡化了命題，只需證eax>ln(ax+1)即可.

三、解法反思

利用導數(shù)證明不等式構造函數(shù)的思維切入點：

1.對不等式f(x)>0含有參數(shù)a的處理策略

(1)利用參數(shù)的范圍對原不等式進行放縮，相應構造不含參函數(shù)，再進行證明.

(2)比較含“a”的結構與含“x”的結構，考慮是否更換主元，構造函數(shù)y=h(a)，轉(zhuǎn)化為證明h(a)>0.

(3)觀察“a”的結構，是否可以對f(x)>0進行分離參數(shù)，等價變形為g(a)>h(x)，進而構造函數(shù)h(x)，把問題轉(zhuǎn)化為求h(x)的最值.

2.觀察不等式f(x)>0的結構

(3)證明“x∈(m,n)，f(x)>0”，將區(qū)間端點m代入是否有f(m)=0，若是可以進一步分析y=f(x)單調(diào)性，定出f(x)最值.

(4)若不等式中出現(xiàn)“et,t,lnt”的結構，分析是否出現(xiàn)“tet與tlnt”、“tet與t+lnt”、““t+et與t+lnt”(tlnt=elntt，tet=et+lnt)的結構，可以利用換元法化簡原不等式的結構.

四、同步訓練

1.(龍巖市2021年高中畢業(yè)班第三次教學質(zhì)量檢測22題)已知函數(shù)f(x)=xex-sinx-1.

(1)證明：f(x)在區(qū)間(-1,+∞)存在唯一極小值點；(2)證明：lnx

分析：(1)略；(2)觀察到不等式中函數(shù)類型有三類，利用不等式x>0,x>sinx放縮，把問題轉(zhuǎn)化為證明x+lnx+1-xex<0，而新的不等式中出現(xiàn)了“xex與x+lnx”，因此利用換元法令t=x+lnx，把問題進一步轉(zhuǎn)化為證明et≥t+1.

3．(2021年云南昆明市高三二模(文))已知函數(shù)f(x)=ax-sinx，x∈(0,+∞)(a∈R).

(1)若f(x)>0，求a的取值范圍；

(2)當a=1時，證明：2f(x)+cosx>e-x.