基于數值仿真的X波段極化SAR海雜波統計建模與特性分析

杜延磊, 高 帆, 劉 濤, 楊 健,*

(1. 中國科學院空天信息創新研究院, 北京 100101; 2. 清華大學電子工程系, 北京 100084;3. 海軍工程大學電子工程學院, 湖北 武漢 430033)

0 引 言

海雜波是制約極化合成孔徑雷達(synthetic aperture radar,SAR)海上目標檢測和識別性能的主要因素之一,其物理機制復雜,且受雷達系統參數、觀測幾何參數及環境物理參數等諸多因素的影響,從而導致對其特征描述和抑制的難度大[1-2]。特別在中高海況的復雜海面條件下,對海雜波統計特性了解的欠缺成為在該背景下極化SAR海面目標檢測、識別和跟蹤困難的主要問題。因此,深入了解極化SAR海雜波的統計分布特性有利于改善雜波抑制效果,提升對海面弱小目標檢測性能,這對基于極化SAR的海面目標探測預警、跟蹤識別、海上救援等軍事和民用都具有重要意義。

極化SAR海雜波是隨機粗糙海面在各個極化通道對入射雷達電磁波的后向散射回波,因此,對極化SAR海雜波的統計建模和特性分析的前提是獲得大量不同極化狀態和參數條件下的海面回波數據。目前,獲得海雜波的手段主要分為兩類:一類是通過岸基或機載平臺對海雜波進行實測獲得;另一類則主要基于海面形態建模和電磁散射求解的理論方法對海雜波進行數值仿真[3]。前者的優點在于所獲得的海雜波數據真實準確,基于此所構建的雜波模型對特定設備和特定應用場景的針對性更強,實用性更好。因此,為了提升各型海用雷達裝備的海上目標探測能力,國內外開展了豐富多樣的雷達海雜波測量試驗,丁昊等對此進行了較為系統全面的介紹[1,4]。然而,海雜波的測量試驗成本較高,且受限于試驗所用的設備、平臺性能以及所在的海域和時機,只能獲得特定場景和參數條件下的海雜波數據[1]。而海雜波的數值仿真則具有較好的靈活性和普適性,可以一定程度上彌補實測試驗的不足。這類方法首先利用海面形態建模方法生成隨機粗糙海面,進而通過數值方法求解其散射方程(低頻類方法)[5]或通過引入近似假設獲得海面遠場散射場的解析近似解(高頻類方法)[6-7]。目前,在實際的海雜波研究中,上述兩類海雜波獲取手段可以實現相互驗證、相互補充[1]。

海雜波的統計分布模型是極化SAR海上目標檢測的重要先驗知識[8-9]。對海雜波統計建模的研究經歷了從高斯性到非高斯性、從單一極化到多極化、從純統計模型到物理/統計結合模型的發展過程[2,10]。較早提出的幾種適用于低分辨率單一極化海雜波的典型分布模型包括Rayleigh分布、Log-normal分布、Weibull分布、K分布等[2,11]。而隨著SAR技術的發展,早期的雜波分布模型難以準確描述較高分辨率的極化SAR海雜波,尤其是其較長的拖尾表現出顯著的非高斯性[2]。目前,復合高斯模型(又稱乘積模型或紋理模型)是最為常用的一類極化SAR海雜波統計分布模型,其假設雷達雜波的散射向量可以分解為兩部分的乘積,一是描述目標后向散射截面(radar cross section, RCS)空間變化的紋理特征,另一是服從復高斯分布的斑噪向量,并通過選擇不同的紋理分布模型,形成各種具體的極化SAR海雜波模型[10]。

海雜波分布模型的參數估計也是其統計建模的關鍵問題之一。傳統的參數估計方法主要包括最大似然估計方法和矩估計方法[11-12]。其中,利用最大似然估計參數時往往需要用到數值方法進行迭代求解,計算效率低[12]。而矩估計方法的特征函數基于Fourier變換獲得,在分布模型較為復雜的時候難以甚至無法獲得解析形式的特征函數,此外,基于矩的估計方法對數據敏感性也常常較高,參數估計的精度較低[13]。針對SAR海雜波的乘積模型,Nicolas通過利用Mellin變換替換Fourier變換來構建新的特征函數和累積量生成函數,從而在此理論框架下構建Mellin類統計量,并基于此進行海雜波模型參數估計,具有計算簡單、精度高、通用性好的特點[14-15]。

目前,對海雜波特性的研究主要利用實測數據的建模分析,而基于具有一定普適性的數值仿真建模研究相對較少,有限的相關研究存在海面仿真尺寸較小、極化信息不足的問題,且對所獲得雜波數據的統計建模和分析方法較為陳舊。鑒于此,本文利用成熟的Apel海浪譜模型,結合Monte Carlo方法仿真生成不同風速下的大尺寸二維粗糙海面,進而利用結合了物理光學(physical optics, PO)模型和彈跳射線法(shooting and bouncing ray,SBR)的電磁散射模型對多極化多角度的海雜波進行仿真,最后基于Mellin類統計量對仿真結果進行統計建模和特性分析。

1 極化SAR海雜波數值仿真模型

1.1 二維粗糙海面建模

粗糙海面的空間形態建模是開展極化SAR海雜波數值仿真和分析的基礎。目前,海面形態建模最常用的方法是基于海浪譜模型的Monte Carlo方法,其假設隨機粗糙海面由無數的諧波疊加而成,從而可以通過對海浪譜先濾波再進行逆Fourier變換獲得海面的高度起伏,因此,該方法也被稱為線性濾波方法[5,16]。基于此,二維粗糙海面高度f(x,y)可以表達為如下的Fourier級數展開:

(1)

式中:Lx和Ly分別為二維海面的長寬,bmn為高斯隨機變量。由于實際的海面仿真中,海面的仿真尺寸和剖分密度是有限的,其決定了對海浪譜濾波的上下限,并具有如下關系[17-18]:

(2)

(3)

此外,根據式所示的海面高度Fourier級數展開特性,可以獲得其系數bmn的周期性和共軛對稱的特性,即

b(m+M)(n+N)=bmn

(4)

(5)

進而結合粗糙面協方差的定義可以推導獲得bmn為[5]

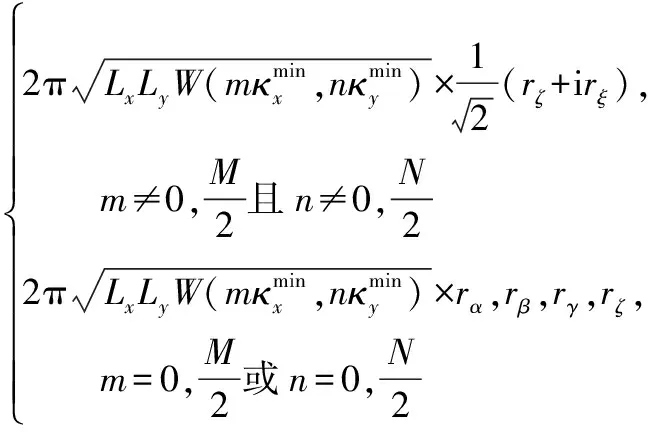
(6)

圖1所示為利用Apel譜和Monte Carlo方法生成的風速為6 m/s下的二維粗糙海面。

圖1 利用Apel譜和Monte Carlo方法生成的6 m/s風速下二維粗糙海面Fig.1 Two-dimensional rough ocean surface at 6 m/s generated using Apel spectrum and Monte Carlo method

1.2 海面電磁散射計算

基于Monte Carlo方法生成的二維粗糙海面,采用理論的電磁散射方法對海面雜波信號進行仿真。現有常用的海面電磁散射計算方法大致可以分為低頻方法和高頻方法兩大類[11]。低頻方法主要是以矩量法[5]、時域有限差分法[22]、有限元法[23]等為代表的數值方法,其通過數值求解粗糙面問題的散射場,具有精度高、適用性廣的優點,但由于其計算量巨大,實際中只能在較低的頻段使用[24]。而高頻方法在粗糙面散射問題的求解中通過引入一定的近似假設,從而獲得散射場的解析形式表達,可以在特定應用范圍內獲得較為準確的結果,且求解速度快。

由于本文主要關注3～5級海況下海面X波段的極化SAR海雜波特性,在此條件下,二維粗糙海面的尺寸和起伏都遠遠大于入射波波長,高精度的低頻數值方法須求解巨量的未知數,對計算資源的消耗巨大,難以滿足三維問題下的海雜波仿真需求[24]。因此,本文采用高頻方法PO方法和SBR方法以分別考慮粗糙海面的單次散射和多次散射,從而開展極化海雜波的仿真。此外,由于海水具有較大的介電常數,對海面模型采用理想電導體假設[25]。

考慮如圖2所示的海面散射場景,入射電磁場Ei、Hi照射到海面一小面元s′,并形成散射場Es、Hs,并定義以海面模型質心為原點的三維坐標系O′X′Y′Z′。根據Maxwell方程組,散射場可由Stratton-Chu方程表達為[7]

圖2 海面散射幾何示意圖Fig.2 Geometric configuration of ocean scattering

(7)

由于Stratton-Chu方程包含面積分項,無法獲得精確的解析解,因此需要引入一定的近似假設,對方程進行簡化求解。為求解Stratton-Chu方程,PO法引入3個近似假設[7]。① 高頻近似:假設入射波波長遠小于目標尺寸,從而近似認為入射波只具備粒子性,忽略其在粗糙面棱邊及邊緣繞射等電磁波波動性,且認為總的散射場僅由粗糙面上被入射波照射到的小面元散射場疊加而來,即,被遮擋的面元對總散射場無貢獻。② 遠場近似:假設散射場觀測點遠離目標粗糙面,且二者距離也遠大于粗糙面尺寸,即|r|?|r′|。③ 切平面近似:假設目標表面任意一點及其附近表面曲率半徑比波長大得多,可以近似為平面。

基于上述三個近似假設,PO法可給出單站條件下(入射波方向i和散射波方向s相反,即i=-s)粗糙面元s′的后向散射場為

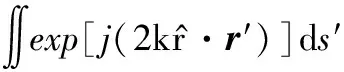
(8)

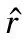
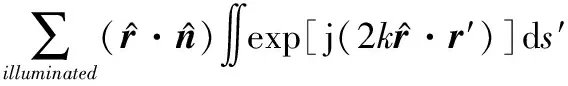
(9)

式中:面積分項可以利用斯托克斯公式進行計算,得到解析表達式為[26]

(10)

(11)

式中：l1,l2,l3分別表示三角面元s′的3條邊矢量。

由式(9)可以發現,后向散射場的極化方向與入射場一致,因此,PO法無法給出交叉極化下的散射系數。鑒于此,本文進一步采用SBR方法來計算粗糙面的多次散射。

(12)

類似的,根據幾何關系,可以獲得第n次反射的入射波方向為

(13)

式中:I為單位矩陣。基于確定的反射路徑和PO法,可以獲得單站條件下,最終的SBR多次散射場為[27]

(14)

基于上述針對海面單次散射和多次散射計算獲得單站散射場,最終接收天線端的總散射場表示為

(15)

(16)

式中：A表示仿真海面像元內雷達波照射面積；θi為雷達入射角。為了仿真分析極化SAR幅度圖的海雜波統計特性[15,28]，本文后續主要采用如下定義的后向散射系數的幅度進行統計建模：

(17)

對于極化SAR系統而言,入射電場和散射電場也可由散射矩陣建立如下關系[8]:

(18)

式中:下標v和h表示水平極化和垂直極化;S為散射矩陣,也可以表達為向量形式為

s=vec(ST)=[Shh,Shv,Svh,Svv]T∈Cd

(19)

式中:vec(·)表示矩陣向量化操作;(·)T表示轉置;d為向量維度。

2 基于Mellin類統計量的雜波建模

2.1 極化SAR海雜波的典型乘積模型

基于前文所介紹的海雜波數值仿真方法,可以計算獲得成像單元內極化SAR散射向量s,其協方差矩陣定義為

Σ=E{ssH}

(20)

式中:E{·}表示期望;(·)H表示Hermitian(轉置共軛)操作。對于視數為L的多視處理數據而言,多視極化協方差矩陣C為[15]

(21)

式中:Xf0表示矩陣正定;C表示復數集。

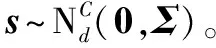
而隨著雷達技術的發展,SAR圖像的空間分辨率得到了顯著的提升,傳統的Gaussian統計模型越來越難以滿足對高分辨率、非均勻海雜波的描述,尤其是大量數據表明海雜波分布的長拖尾表現出顯著的非高斯特性[2]。因此,諸多學者提出了一類復合Gaussian海雜波統計分布模型,又稱為乘積模型或紋理模型。這類模型假設雷達雜波的散射向量可以分解為兩部分的乘積,一是描述目標后向散射截面空間變化的紋理特征,另一是服從復高斯分布的斑噪向量,并通過選擇不同的紋理分布模型,形成各種具體的極化SAR海雜波模型[10]。

假設SAR海雜波各極化通道的紋理變化特性相同,則分辨單元內的散射向量k可以寫作:

(22)

式中:τ為紋理參數,其均值為1;s與前文定義一致,表示斑噪向量。對于多視數據,其極化協方差矩陣表示為

(23)

對于給定的τ,散射向量k和極化協方差矩陣C的概率密度函數(probability density function, PDF)分別為[10]

(24)

(25)

式中:tr(·)表示矩陣的跡；Γd(L)為歸一化因子,定義為

(26)

式中:Γ(·)表示gamma函數。

當紋理分布p(τ)已知時,海雜波分辨單元內散射向量k和極化協方差矩陣C的PDF為

(27)

(28)

目前,為了描述不同場景的極化SAR數據的雜波信號,學者們通過引入不同的紋理分布模型提出了多種極化SAR雜波的復合Gaussian統計模型。本文總結了其中較為常用的幾種典型雜波分布統計模型,包括K分布、G0分布、Kummer-U分布、W分布、M分布等,表1給出了這幾種分布模型紋理參量τ、散射向量k和極化協方差矩陣C的PDF。特別地,對于Wishart分布而言,可以認為其紋理模型為常數,即p(τ)=δ(τ-1)。

表1中,式(32)中的Kν表示ν階第二類修正Bessel函數,式(34)中U(a,b,z)為第二類合流超幾何函數,式(35)中W為Whittaker W函數,其為合流超幾何函數U(a,b,z)的函數,式(36)中M為第一類合流超幾何函數,亦即Kummer-M函數[10]。

2.2 Mellin類統計量的定義與計算

對于所獲得的一組雜波數據,其統計建模一般來說包括兩個部分,一是確定其分布模型,二是對所確定分布模型的參數進行估計。在極化SAR海雜波研究中,在經過早期利用簡單的Rayleigh分布、Log-normal分布、Weibull分布等純統計模型的發展之后,越來越多的研究認為中低分辨率條件下,極化SAR海雜波可以用K分布來描述,并基于此發展了大量K分布參數估計方法。其中,傳統的參數估計方法主要包括最大似然估計方法和矩估計方法[11-12]。而利用最大似然估計參數時往往需要使用數值方法進行迭代求解,計算效率低。因此,基于矩的參數估計方法得到了廣泛地使用。

矩估計方法的數學理論基礎是:對于給定隨機變量的分布函數,其特征函數可以表示為關于矩的級數展開形式,當該分布所有矩存在且有限,且其特征函數的冪級數展開在靠近原點處收斂,則該分布函數可由其特征函數唯一表示[15]。然而,矩估計方法的特征函數是基于Fourier變換獲得,在分布模型較為復雜的時候難以甚至無法獲得解析形式的特征函數,此外,基于矩的估計方法對數據敏感性也常常較高,參數估計的精度較低[28]。因此,本文采用基于Mellin類統計量的方法來估計雜波分布模型的參數。

不同于傳統參數估計方法的特征函數基于Fourier變換,Mellin類統計量的定義與計算采用Mellin變換。對于復矩陣元函數f(Z),其Mellin變換定義為[15]

(29)

基于Mellin變換,矩陣變量Z的Mellin類特征函數(characteristic function, CF)φZ和Mellin類累積量生成函數(cumulant generation function, CGF)φZ定義為

φZ(χ)=E{Zχ-d}=M{pZ(Z)}(χ)=

φZ(χ)=ln[φZ(χ)]

(30)

進一步地,根據矩量和累積量的定義,Z的v階Mellin類矩μv(Z)和v階Mellin類累積量υv(Z)分別定義為

(31)

由(31)式可以發現μv(Z)=E{lnZ},因此Mellin類矩也被稱為對數矩,類似的,Mellin類累積量也被稱為對數累積量。當Z的所有對數矩和對數累積量存在時,有

(37)

對數矩量和對數累積量之間可以由Faadi Bruno公式的組合形式表示為[29]

(38)

從而可獲得Z的前三階Mellin類累積量為

(39)

2.3 基于Mellin類統計量的雜波模型參數估計

為了使用Mellin類統計量對海雜波模型參數進行估計,我們需要推到獲得二者之間的嚴格關系。假設乘積模型的極化協方差矩陣寫作:

(40)

(41)

(χ-d)ln|Σ|-(χ-d)dlnL

(42)

(43)

進一步地,對于紋理分量T,其Mellin類特征函數為

(44)

結合Mellin統計量定義和Faá di Bruno公式可得:

(45)

由于隨機矩陣變量X=UV的Mellin類特征函數和統計量有如下性質[14]:

(46)

因此,乘積模型極化協方差矩陣C的Mellin類累積量為

(47)

代入式(43)最終有:

(48)

式(48)給出了極化SAR雜波的Mellin類累積量與乘積模型參數之間的關系,基于此,我們可以利用式(38)計算雜波數據的若干階累積量,從而可以對雜波分布模型參數進行估算。對于式(48)中紋理模型的Mellin類統計量,表2給出了K分布、G0分布、Kummer-U分布、W分布、M分布等乘積模型的紋理分布對數累積量。

表2 典型紋理分布模型的對數累積量Table 2 Log-cumulants of typical texture distribution models

此外,在理論上,這5種典型乘積模型可以嚴格地劃分二階和三階Mellin類累積量所形成的平面空間,如圖3所示[9]。因此,利用樣本數據的Mellin類統計量還可以判斷雜波數據所服從的分布。

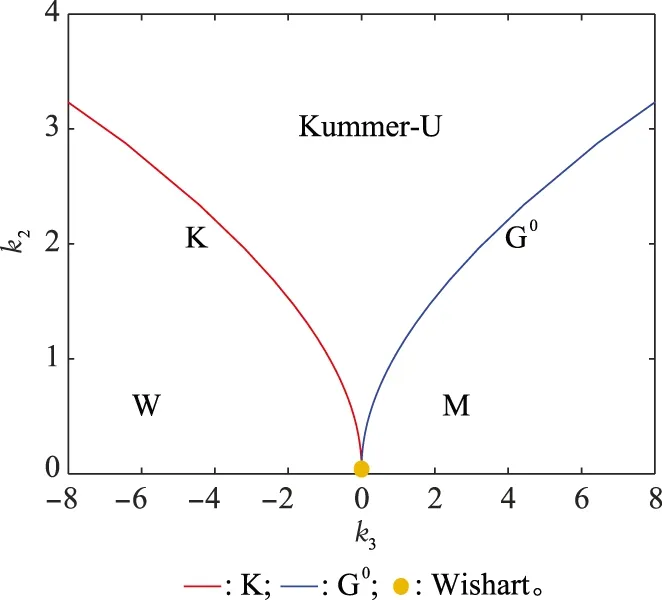
圖3 典型雜波乘積模型在二階/三階Mellin類累積量空間的分布Fig.3 Typical product models in the space of 2nd/3rd Mellin-kind cumulants

3 仿真結果與分析

利用前文介紹的海面形態建模和雷達散射計算高頻方法,我們對海面X波段全極化海雜波進行數值仿真,并基于Mellin類統計量方法開展海雜波統計建模和特性分析。

由于本文旨在對3～5級海況下海面X波段(9.6 GHz)高分辨率極化海雜波進行仿真建模和統計分析,因此,我們首先基于Apel海浪譜和Monte Carlo方法分別生成了6 m/s、9 m/s和12 m/s風速下的二維粗糙海面,如圖4(a)所示。所生成海面的尺寸為128 m×128 m (4 096λ×4 096λ,λ為入射波波長),其中,為了仿真海面大尺度海浪,生成真實的中高海況海面,在海面仿真的過程中,本文使用了包含譜峰的海浪能量譜,這使得生成的海面包含了所有的大尺度風浪,同時也使得仿真海面尺寸范圍較大,遠遠大于現有的低頻數值仿真方法可以實現的大小。尤其在仿真12 m/s風速下海面時,為了包含海浪譜的譜峰,則生成的海面尺寸達到256 m×256 m。在后續的海面電磁散射計算中,為了與其他兩個風速海面具有可比性,也為了減少運算量,我們對12 m/s風速海面進行裁剪,獲得尺寸為128 m×128 m的海面模型。由圖4(a)可以看出,隨著風速增大,海面的粗糙起伏也逐漸變大,在本文的案例中,所生成的6 m/s、9 m/s和12 m/s風速下的海面均方根高度分別為6.13λ、12.80λ和19.88λ。此外,圖4(a)中,風向由y軸正坐標指向負坐標。為了保證對海面刻畫以及電磁散射仿真的精度,并考慮到海面小尺度粗糙度對雷達后向散射的影響,本文所仿真海面的剖分密度達到4個采樣點/λ。

圖4 不同風速下的二維粗糙海面和對應的雷達后向散射系數Fig.4 Rough ocean surfaces at various wind speeds and corresponding radar backscattering coefficients

基于所生成的不同風速二維粗糙海面,本文利用所建立的海面電磁散射高頻仿真方法開展不同雷達入射角和方位角條件下X波段全極化海雜波數值仿真計算。在實際的計算中,根據SAR的成像空間分辨率概念,我們將海面剖分為64×64個大小為2 m×2 m的成像單元。圖4(b)所示為入射角為20°、雷達方位角為逆風方向條件下,本文所計算的不同風速下二維海面X波段的VV極化雷達后向散射系數。由圖可以發現,隨著海面風速的增大,海面的雷達后向散射系數也增大,這與海面粗糙度增大,海面雷達散射增強的基本常識相符合。此外,考慮到雷達觀測方向為逆風方向(沿y軸負坐標指向正坐標),由圖4(a)和圖4(b)可以發現,海面迎向入射波的面元后向散射系數較大,這與粗糙面雷達散射特性相一致。

3.1 仿真海雜波的后向散射系數與分布驗證

在開展海雜波的建模和分析之前,我們需要對仿真海雜波的后向散射系數和統計分布準確性進行驗證。本文選擇X波段廣泛使用的并由實測數據擬合獲得的地球物理模式函數XMOD-2對仿真海雜波的同極化后向散射系數進行驗證[30]。對于交叉極化,受限于目前較少的X波段交叉極化實測數據,我們采用Voronovich和Zavorotny在文獻中給出的二階小斜率近似模型(SSA-2)結果和測量數據對仿真海雜波的交叉極化后向散射系數進行驗證[31-32]。圖5所示為仿真海雜波后向散射系數與XMOD-2、SSA-2模型結果及實測數據的對比。

圖5 利用其他模型和實測數據對仿真海雜波后向散射系數精度進行驗證Fig.5 Accuracy validation of simulated sea clutter using other models and measurement

由圖5可以看出,在同極化條件下,仿真海雜波的后向散射系數與XMOD-2模型有較好的吻合,最大誤差不超過2 dB,這表明本文采用的海面雷達散射高頻方法在同極化條件下對X波段海雜波具有較高的仿真精度。而對于交叉極化,盡管在高風速情況下仿真海雜波后向散射系數與SSA-2模型結果較為接近,但在低風速情況下,仿真結果則與參考數據有相對較大的誤差,最大可達約10 dB。考慮到海面交叉極化后向散射能量遠遠低于同極化,且本文主要關注中高海況下海雜波的統計分布及定性的特性分析,這一誤差大小對于交叉極化仿真是可以接受的。

為了驗證數值仿真所得到海雜波的分布特性準確性,我們利用實測的海雜波分布與仿真海雜波分布進行對比。本文采用由岸基X波段固態功放監視/導航雷達于2021年1月6日15時6分利用凝視模式獲得的海面雜波數據,該數據由海軍航空大學的“雷達對海探測數據共享計劃”發布,并包含了同步測量的氣象水文等輔助資料。獲得實測數據的雷達中心頻率為9.4 GHz,極化方式為HH極化,距離分辨率為6 m,入射角為80°,雷達觀測方位角為55.05°,其他的雷達系統參數在文獻[3,33]具體給出。此外,根據與同步測量的海洋氣象水文數據進行時空匹配,可知所測海雜波數據對應海面的風速為9.57 m/s,風向為61.73°,因此,考慮到雷達觀測方位角,雷達觀測方位相對于風向約為6.68°。

由于實測海雜波數據是未經輻射定標的散射強度結果,與仿真數據雷達后向散射系數無法進行直接對比,因此,本文對仿真和實測海雜波數據的進行了歸一化處理,并基于歸一化后的海雜波數據計算了其前三階對數累積量,圖6(a)所示為實測和仿真海雜波數據的二階/三階對數累積量對比。由圖中散點分布可以看出實測和仿真海雜波具有非常相近的分布特征,且較為服從Wishart分布,這表明在此條件下,所獲得的海雜波紋理特性并不顯著,考慮到本案例較大的雷達入射角,這一特性是較為合理的。

圖6 仿真海雜波分布與實測海雜波分布的對比Fig.6 Comparison of distributions of simulated sea clutter and measured sea clutter

基于圖6(a)結果,我們采用K分布模型對歸一化實測和仿真海雜波的雷達后向散射系數和散射場幅度的概率密度分布進行擬合,并利用所計算的二階/三階對數累積量對模型參數進行估計,最終仿真和實測海雜波分布的對比如圖6(b)所示。可以看出,仿真海雜波與實測海雜波的分布具有良好的匹配,證明了利用前文的海面雜波高頻數值仿真方法對海雜波分布仿真的準確性,以及利用Mellin類統計量開展海雜波統計分布和特性分析的可行性。

在本文的海雜波數值仿真中,盡管我們通過采用包含海浪譜譜峰考慮了所有大尺度風浪的貢獻,但是小尺度波浪的貢獻則由于剖分密度的限制進行了一定的截斷。由式可知,4個采樣點/λ的剖分密度表明海面波數大于402 rad/m的小尺度波浪在仿真海面中被舍去。因此,對于本文采用的電磁散射方法和海面剖分密度是否足以描述海浪細節對海雜波的貢獻,尤其在5級高海況條件下,需要進一步進行驗證。圖7給出了5級海況下,分別利用4個采樣點/λ和8個采樣點/λ仿真海面獲得的海雜波的二階/三階對數累積量及分布對比。特別地,這里海雜波的仿真像元大小為1 m×1 m。由圖7(a)可以看出,采用不同剖分密度海面獲得的極化SAR仿真海雜波具有相近的二階/三階對數累積量,且兩組海雜波的后向散射系數平均差異在同極化下可以忽略,在交叉極化下僅約0.72 dB。在圖7(b)中,由不同剖分密度海面獲得的海雜波在同極化和交叉極化都分別具有幾乎一致的分布。這表明海面較小尺度的波浪對海面雷達散射的貢獻較小,這也與我們前期的研究結論相符合[17],本文采用4個采樣點/λ的海面剖分密度可以滿足海雜波仿真中對海浪細節的描述。

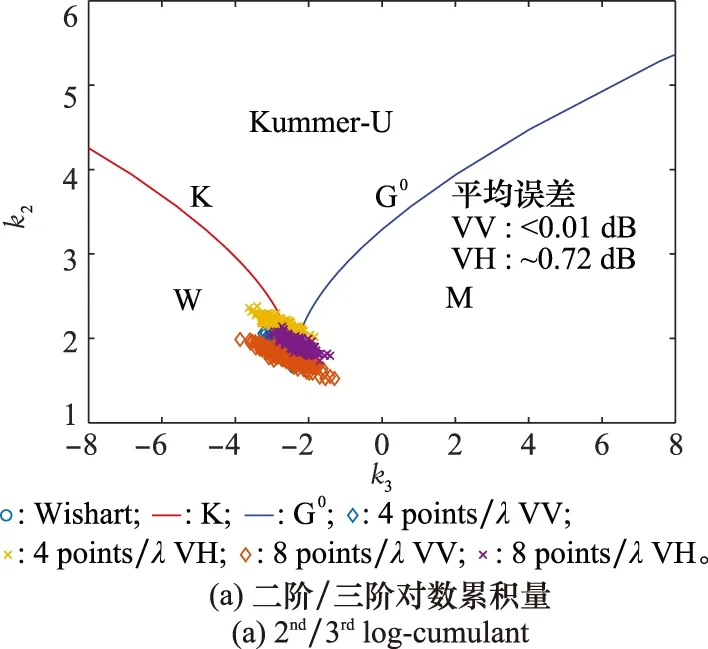
圖7 不同剖分密度海面獲得的仿真海雜波分布對比Fig.7 Comparison of distributions of simulated sea clutters from surfaces with different discretizing density

3.2 X波段高分辨率極化SAR海雜波建模與分析

在海雜波數值仿真的基礎上,我們基于Mellin類統計量構建海雜波的分布模型,并分析了雷達入射角、海面風速風向對海雜波分布的影響。圖8所示為不同風速下X波段同極化海雜波的分布,其中,仿真海雜波的雷達入射角為20°,風向為逆風方向。由圖8(a)首先可以看出,VV極化和HH極化海雜波的二階/三階對數累積量非常接近,這主要是因為雷達入射角較小,VV和HH極化的雷達后向散射系數較為接近,表明VV和HH極化海雜波有著相近的分布,尤其是二者的紋理分布接近,因此在圖8(b)只展示了VV極化結果。進一步地,我們可以發現高分辨率的同極化X波段海雜波并不服從傳統的適用于中低分辨率海雜波的K分布模型,這說明在此條件下,海雜波的紋理特征不服從gamma分布。而在不同的風速下,X波段同極化海雜波表現出不同的紋理分布,并最終使得其服從不同的分布模型。具體來說,6 m/s和9 m/s風速下海雜波分別服從Kummer-U分布和M分布,但二者都比較接近G0分布,在12 m/s風速下,X波段同極化海雜波服從M分布。基于海雜波所服從的分布模型,我們利用所計算的對數累積量對相應的模型參數進行了估計,并在圖8(b)中對比了不同風速下海雜波幅度的概率密度分布。由圖8(b)可以看出,利用圖8(a)所指示的分布模型可以很好地擬合海雜波數據。隨著風速的增大,海雜波分布中后向散射系數幅度較大部分占比逐漸升高,海雜波分布由陡逐漸變緩,這與物理事實相符合。

圖8 不同風速下X波段同極化海雜波的分布Fig.8 Distribution of X-band co-pol sea clutters at various wind speeds

圖9展示了不同風速下X波段交叉極化海雜波的分布,相關的海雜波仿真參數與圖8相同。類似于同極化,HV極化和VH極化海雜波的二階、三階對數累積量也非常接近,考慮到極化互易性原理,這是合理的,因此,在此處及后續的交叉極化海雜波分布模型中,我們僅展示HV極化。而與同極化不同的是,交叉極化海雜波的二階、三階對數累積量在不同風速下都集中在Wishart分布附近,表明交叉極化條件下高分辨率X波段海雜波沒有顯著的紋理特征,因此,在高分辨率條件下,極化SAR海雜波在四個極化通道不適宜使用相同的紋理模型來描述,這與傳統針對中低分辨率海雜波在各極化通道采用相同紋理模型不一致。在圖9(b)中我們利用K分布擬合了不同風速下交叉極化的海雜波分布,與同極化類似,隨著風速的增大,海雜波分布由陡逐漸變緩。

圖9 不同風速下X波段交叉極化海雜波的分布Fig.9 Distribution of X-band cross-pol sea clutters at various wind speeds

圖10所示為不同入射角下X波段同極化海雜波的分布,其中,仿真海雜波的海面風速為9 m/s,風向為逆風方向。由圖10(a)可以看出,雷達入射角對高分辨率X波段同極化海雜波的分布有著顯著的影響,在入射角較小時,同極化海雜波有著顯著的紋理特征,且VV和HH極化的二階/三階對數累積量非常接近。而在雷達入射角較大時,海雜波的紋理特征顯著減弱,且二階/三階對數累積量在VV和HH極化間顯示出差異。在圖10(b)中我們分別利用M分布和K分布擬合雷達入射角為20°、40°、60°時的VV極化海雜波分布,可以看出所用模型可以很好地擬合海雜波分布,由于海面同極化后向散射能量隨著入射角增大而減小,圖中的分布模型也隨著入射角增大而逐漸變陡。

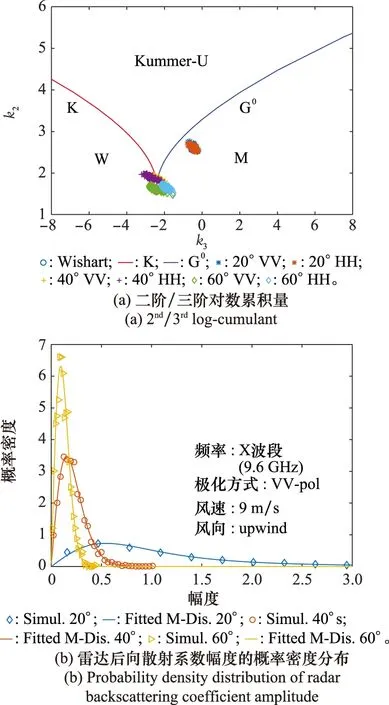
圖10 不同入射角下X波段同極化海雜波的分布Fig.10 Distribution of X-band co-pol sea clutters at various incidence angles

圖11所示為不同風向下X波段同極化海雜波的分布,其中,仿真海雜波的雷達入射角為20°,海面風速為9 m/s。由圖可以看出,該條件下海雜波的二階/三階對數累積量集中在G0分布附近,并在不同的風向下稍有區別。在圖11(b)中,我們分別采用M分布、G0分布和Kummer-U分布對風向為逆風、側風和45°時的海雜波分布進行擬合,可以發現海雜波分布隨著風向由側風向逆風變化逐漸變緩。

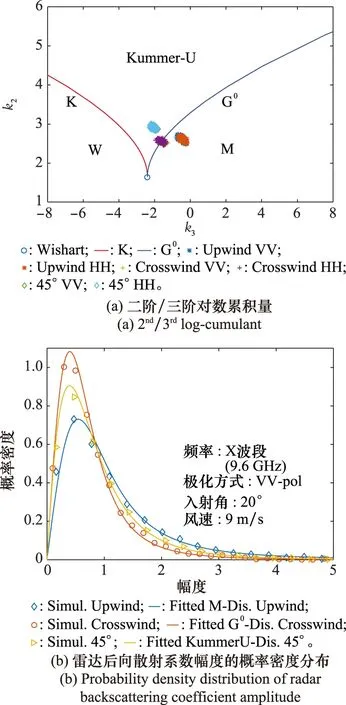
圖11 不同風向下X波段同極化海雜波的分布Fig.11 Distribution of X-band co-pol sea clutters in various wind directions

圖12展示了雷達視數對X波段同極化海雜波分布的影響,其中,仿真海雜波的雷達入射角為20°,海面風速為9 m/s,風向為側風方向。由圖12(a)可以看出,隨著雷達視數的增大,海雜波的紋理特征逐漸減弱,考慮到雷達多視處理的基本原理及其空間濾波的效果,海雜波的紋理特征被平滑是合理的。進一步地,由圖12(b)也可以看出,多視處理使得海雜波的極大值和極小值減少,海雜波的分布逐漸向中間移動。

圖12 不同雷達視數條件下X波段同極化海雜波的分布Fig.12 Distribution of X-band co-pol sea clutters under conditions with various radar looks

4 結 論

中高海況下極化SAR海雜波的統計建模是海面艦船、導彈及相關飛行器檢測預警的關鍵和難點問題。本文針對3～5級海況下X波段極化SAR海雜波開展數值仿真、統計建模與分析研究。首先利用成熟的Apel海浪譜模型和Monte Carlo方法建立了6 m/s、9 m/s和12 m/s風速下二維粗糙海面模型,進而采用高頻方法開展不同風速、風向、雷達入射角、極化方式下的X波段海雜波仿真計算。為了獲得準確的海面極化散射系數,我們采用PO方法和SBR方法以分別考慮粗糙海面的單次散射和多次散射。基于仿真海雜波數據,利用典型的乘積模型和Mellin類統計量開展高分辨率X波段極化SAR海雜波統計建模和特性分析。仿真結果表明:在2 m×2 m的高分辨率條件下,X波段同極化海雜波并不服從適用于中低分辨率海雜波的K分布,且在不同風速風向下呈現出不同的紋理特征;X波段交叉極化海雜波表現出較弱的紋理特征,服從Wishart分布。因此,X波段極化SAR海雜波在同極化和交叉極化條件下具有不同的紋理分布特征,這與傳統針對中低分辨率海雜波在各極化通道采用相同紋理模型不一致。此外,隨著入射角和雷達視數的增大,海雜波的紋理特征逐漸減弱。

盡管本文基于高頻仿真方法和Mellin類統計量對X波段極化海雜波進行仿真建模,給出了海面風速、風向、雷達入射角等雷達系統參數和環境參數對極化海雜波影響的初步分析結果,但受限于模型在交叉極化的仿真精度,相關的分析僅在定性層面展開,未給出定量化的結果。在后續工作中,可進一步構建精細化的海面模型,并考慮海浪尖峰的繞射等現象,提高模型在交叉極化的仿真精度,并在本文工作的基礎上增加仿真數據,建立極化SAR海雜波統計模型與雷達系統參數和海洋環境參數之間的經驗模式函數,服務海面極化SAR海面目標檢測應用。