碰撞振動系統的最大Lyapunov指數計算

黨 慧，馮進鈐，楊 森

(西安工程大學 理學院，陜西 西安 710048)

0 引 言

碰撞、顫碰以及伴隨顫碰所產生的黏滯現象是非光滑系統動力學研究的熱點問題之一。碰撞振動系統在應用數學、應用物理、工程機械等專業領域內皆有涉及。作為一種非光滑系統[1]，它具有較強的非線性特征，在動力學研究中產生了較為深遠的影響。碰撞振動系統通常表現為存在間隙的各活動部件之間或者活動部件與固定部件之間的反復沖擊與碰撞[2]。借助于現代動力系統理論對碰撞振動系統的研究，主要集中于該系統的周期運動、分岔和混沌等[3-6]。

由于碰撞所導致向量場的不連續性，碰撞振動系統在發生高速碰撞后，在一定條件下可能還會發生顫碰現象。顫碰是碰撞振動系統中的一種新穎的動力學行為[7]。早期，BUDD等研究了線性碰撞振動系統中的顫碰及其相關動力學行為[8]；ALZATE等通過實驗，分析了齒輪系統中的顫碰[9]。文獻[10]主要討論了二自由度碰撞振動系統的周期黏滯運動和顫碰現象；文獻[11]分析了一類二自由度含間隙彈性碰撞系統的顫碰運動特性；文獻[12]研究了顫碰引起的黏滯現象，并利用Simulink進行動力學仿真。

在非線性動力學系統中，Lyapunov指數譜是判定動力系統運動的穩定性和混沌特性的一種重要工具[13-15]。目前，關于光滑動力系統的Lyapunov指數譜研究已較成熟：WOLF等利用實驗時間序列提出了Lyapunov指數譜的通用算法，并對該算法進行了實驗驗證[16]。針對特殊的非光滑系統，STEFANSKI將映射同步用于估計確定性碰撞系統的最大Lyapunov指數[17]；GALVANETTO根據映射法則，推導計算了幾種不連續映射系統Lyapunov指數的數值結果[18]。FENG等考慮了在不同的隨機噪聲激勵下時，碰撞振動系統的隨機響應現象[19]。近幾年，LI等研究了混合動態系統的Lyapunov穩定性切換[20]；張艷龍等給出了隨機干擾強度下的二自由度碰撞振動系統的Lyapunov指數的計算推導[21]；李得洋等結合系統分岔圖、相圖和Lyapunov指數譜, 分析了系統周期運動的穩定性與各種分岔行為[22-23]。

上述Lyapunov指數的計算方法都未考慮碰撞振動系統中的顫碰以及黏滯現象，本文研究具有顫碰或黏滯現象的最大Lyapunov指數的計算，并通過算例說明計算方法的正確性。

1 碰撞振動系統的運動狀態

考慮一般二維碰撞振動系統

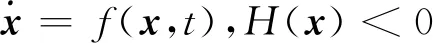
(1)

對應的碰撞映射為

x+=R(x-),H(x)=0

(2)

式中:x∈D?R2,t∈R+;f為系統無約束時的向量場函數；R為碰撞映射；H(x)表示系統的運動軌線與約束面Σ之間的距離。式中下標-、+分別表示系統碰撞前后的時刻。

為了描述方便，引入碰撞面

ΣI={x∈D:H(x)=0}

(3)

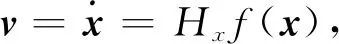
(4)

(5)

當系統發生顫碰現象并從顫碰進入黏滯運動時,系統的運動過程可能存在4種運動形式,如圖1所示。

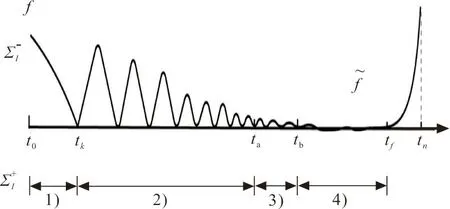
圖1 運動過程示意圖Fig.1 Diagram of motion process

3) 低速碰撞到顫碰：ta→tb。大量高速碰撞后，系統可能出現顫碰運動。如圖1所示，系統從ta時刻進入無限次碰撞，隨著振幅的逐漸減弱，最終v→0。系統運動狀態由x∈Σta={x:H(x)=0,|v|<ε?1}切換到x∈Σtb={x:H(x)=0,v=0}。為方便計算，引入彗尾映射PC,滿足

xb=PCxa

(6)

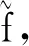
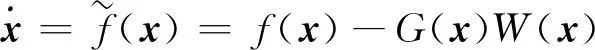
(7)

式中:W(x)=(0,-(r+1))T,

如圖1所示，當t∈[ta,tb]時系統進行顫碰運動，在tb時刻開始進入黏滯,當t∈[tb,tf]時系統進行黏滯運動。由于在tf時刻，加速度a=0，故系統在此時開始逃離黏滯。相應地，此時系統的運動狀態由x∈Σ[tb,tf]{x:H(x)=0,v=0,a>0}切換到x∈Σ[tf,tn]{x:H(x)=0,v=0,a<0}，而當t∈[tf,tn]時系統又開始作“自由”運動。

2 最大Lyapunov指數

根據上述4種情況(見圖1)，系統的運動狀態可由連續微分方程和離散映射進行描述。易知在1)和4)情況下系統的運動由連續微分方程描述，而在2)和3)情況下系統的運動則由離散映射進行刻畫。

情形Ⅰ：連續微分方程。假設系統運動方程滿足

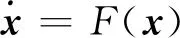
(8)

考慮對參考軌道x0(t)的一個擾動δ(x)，x=x0+δ(x)，并滿足

(9)

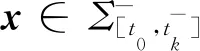
Fx(x0)=(fij)2×2=fx(x0)

(10)

(ⅱ) 當x∈Σ[tb,tf]時，系統作黏滯運動，由式(7)可知

(11)

式中:

(12)

(13)

引入Khasminskii變換

(14)

將式(9)帶入式(14)中化簡可得

(15)

情形Ⅱ：離散映射。引入離散映射P，使系統運動狀態滿足

P:xn→xn+1

(16)

考慮對參考軌道x0的一個擾動δ(x)，x=x0+δ(x)，并滿足

δ(xn+1)=DPδ(xn)

(17)

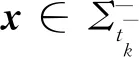
(18)

(ⅱ) 當x∈Σta時，

(19)

式中:

PC(x)=x+M1(x)+M2(x)

(20)

(21)

故

(22)

(23)

式中:f1(x)=v=Hxf(x)，f2(x)=a=(Hxx+Hxfx)f(x)。

引入Khasminskii變換，將式(17)帶入式(14)中，化簡可得

(24)

根據動力學理論，最大Lyapunov指數可表示為

(25)

式中‖·‖皆為2范數。

系統在上述4種運動狀態下的最大Lyapunov指數可劃分為連續微分方程及離散映射2部分進行描述。將式(10)、式(11)分別帶入式(15)，式(18)、式(19)分別帶入式(24)，并由式(25)可知

(26)

分析式(26)可知:式中第1項為系統處于階段1),即做無約束運動時的Lyapunov指數；第2～4項分別為系統處于階段2)～4)時,對系統Lyapunov指數的補充項，即分別為系統處于高速碰撞、顫碰運動以及黏滯運動。

3 算 例

3.1 系統的分岔與Lyapunov指數比較

考慮諧和激勵下單邊碰撞振動系統，非對稱結構的形狀記憶合金梁模型遵循如下方程[25]：

(27)

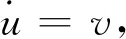
(28)

式中:r為碰撞恢復系數;h為碰撞約束位置；k為線性剛度系數；α為非線性剛度系數；μ為阻尼系數；γ為負阻尼系數；fcos(ωt)為諧和激勵。

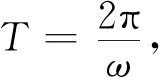
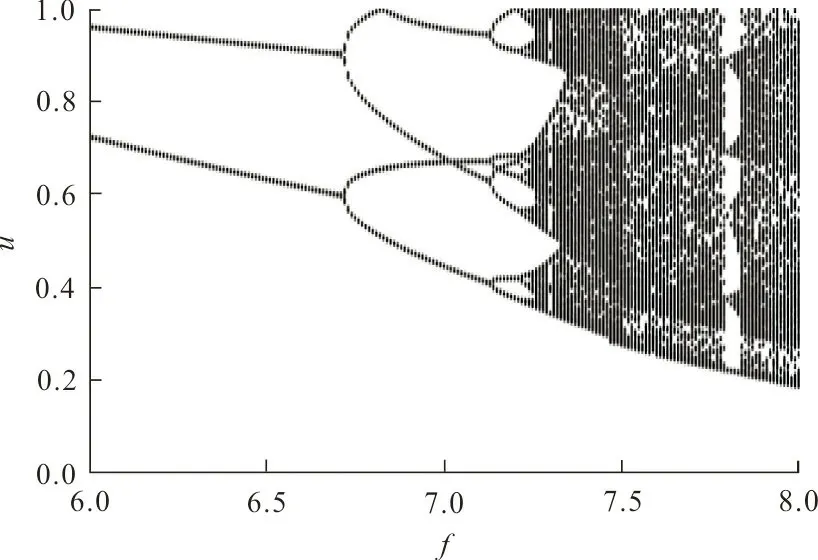
(a) u隨參數f變化分岔

3.2 顫碰、黏滯運動的Lyapunov指數

為了驗證系統(27)在顫碰以及黏滯情形下Lyapunov指數計算式(26)的有效性，固定系統部分參數r=0.8，k=1.0，α=1.0，μ=0.2，γ=0，ω=0.2，取初始值為(-1.5,0)T。圖3給出了系統從顫碰到黏滯再到黏滯運動消失的時間歷程圖和最大Lyapunov指數序列圖。當f=1.5時，圖3(a)顯示了系統作周期運動，存在顫碰和黏滯。從圖3(c)中可以看到：當系統由顫碰切換到黏滯運動時，最大Lyapunov指數發生了跳躍，呈現出非光滑結構；當系統逃離黏滯，重新作“自由”運動時，最大Lyapunov指數并未發生明顯跳躍，呈現出近似“光滑”結構。當f=0.81時，由圖3(b)可見，系統運動過程為非周期的，圖3(d)中系統的最大Lyapunov指數僅發生一次跳躍，發生跳躍的時刻與圖3(b)中黏滯開始時刻同樣保持一致。

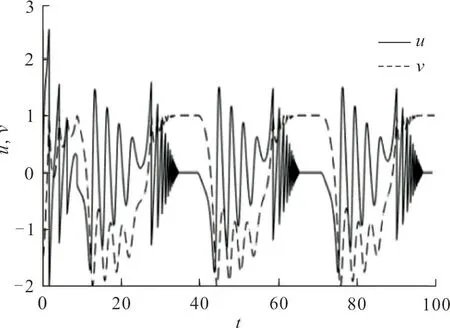
(a) 時間歷程(f=1.5)

圖4給出了系統的相圖和與其對應的最大Lyapunov指數收斂序列圖。

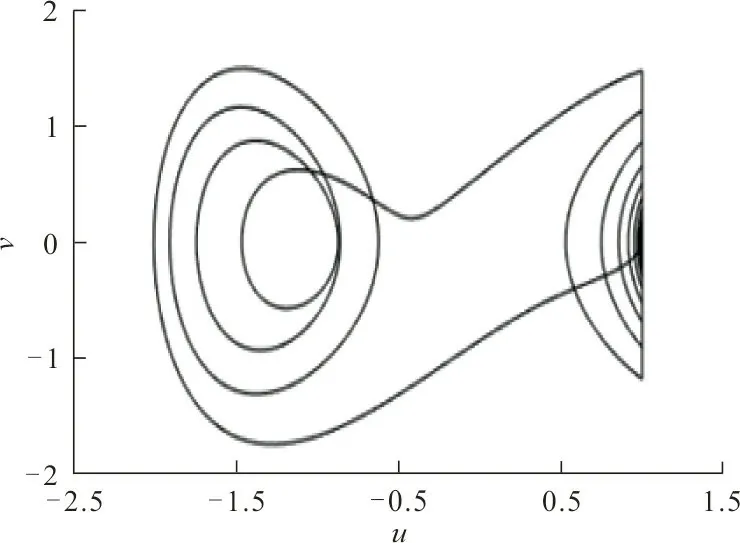
(a) 相圖(f=1.5)

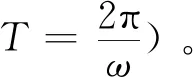
4 結 語

利用不連續映射和彗尾映射對系統碰撞和顫碰的運動特性進行了有效近似，提出了系統在連續微分方程以及離散映射下的最大Lyapunov指數的計算方法。以形狀記憶合金梁模型為例，討論了系統的最大Lyapunov指數。同時，數值結果與構造的最大Lyapunov指數計算結果保持一致，驗證了該計算的有效性。研究表明：碰撞振動系統在一定條件下會發生顫碰現象，并隨之發生黏滯運動；最大Lyapunov指數可以有效捕捉系統的分岔、周期窗口和顫碰的切換。