CFRP鉆削有限元仿真及軸向力預(yù)測(cè)

李 晶，韓文東，張銀飛，彭 鎮(zhèn)，曹玲玲

(1.西安工程大學(xué) 機(jī)電工程學(xué)院，陜西 西安 710048；2.紹興市柯橋區(qū)西紡紡織產(chǎn)業(yè)創(chuàng)新研究院，浙江 紹興 312065)

0 引 言

碳纖維復(fù)合材料因其自身優(yōu)良的強(qiáng)度質(zhì)量比、抗疲勞性和耐腐蝕性，是替代傳統(tǒng)材料的良好材料[1-2]。碳纖維復(fù)合材料廣泛應(yīng)用于航空航天、高速列車、汽車、醫(yī)療等領(lǐng)域[3]。為滿足CFRP構(gòu)件的裝配，在CFRP構(gòu)件固化成形后，需要進(jìn)行鉆孔、切邊等機(jī)械加工[4-5]。但是碳纖維復(fù)合材料層間結(jié)合強(qiáng)度較低，鉆削加工中產(chǎn)生的應(yīng)力集中會(huì)導(dǎo)致鉆孔時(shí)產(chǎn)生分層現(xiàn)象。分層損傷會(huì)使得構(gòu)件強(qiáng)度降低，進(jìn)而影響CFRP構(gòu)件的服役壽命[6-8]。

國(guó)內(nèi)外學(xué)者在碳纖維復(fù)合材料鉆削領(lǐng)域有廣泛的研究和成果。SU等提出了一種新的鉆銑復(fù)合工藝，這種鉆銑復(fù)合工藝可以明顯地減少鉆孔階段產(chǎn)生的軸向力以及軸向力引起的損傷[9]。KONG等為了降低CFRP軸向力以及抑制軸向力引起的損傷，提出了一種ODR新型刀具,可以有效地降低軸向力和切削溫度，提高鉆孔質(zhì)量[10]。PHADNIS等為了研究產(chǎn)生損傷時(shí)的臨界軸向力和扭矩，建立了CFRP鉆削三維仿真模型和預(yù)測(cè)模型，得到的預(yù)測(cè)結(jié)果與實(shí)驗(yàn)結(jié)果基本一致[11]。FEITO等開發(fā)了完整的鉆削模型，通過(guò)仿真實(shí)驗(yàn)驗(yàn)證了模型的正確性，并通過(guò)建立分層預(yù)測(cè)模型，發(fā)現(xiàn)CFRP鉆削分層損傷的主要影響因素來(lái)自軸向力[12]。ISBILIR等采用Hashin準(zhǔn)則建立CFRP三維鉆削仿真模型，來(lái)研究切削速度、進(jìn)給量對(duì)軸向力、扭矩和分層的影響[13]。LIU等分析了纖維方向?qū)︺@削的影響和CFRP/金屬疊層的鉆削規(guī)律，建立了不同鉆削階段全周期軸向力的預(yù)測(cè)模型[14]。唐寧等應(yīng)用自適應(yīng)神經(jīng)模糊推理系統(tǒng)對(duì)CFRP鉆削軸向力進(jìn)行了有效的預(yù)測(cè)[15]。UHLMANN等為了研究切削速度、進(jìn)給速度對(duì)刀具磨損、工件質(zhì)量的影響，采用高主軸轉(zhuǎn)速加工CFRP，結(jié)果表明：高速切削CFRP時(shí)，產(chǎn)生的切削力比常規(guī)切削速度產(chǎn)生的切削力低[16]。BONNET等對(duì)CFRP鉆削軸向力進(jìn)行曲線擬合，發(fā)現(xiàn)切削刃與纖維夾角為45°時(shí)，軸向力最大；夾角為135°時(shí)產(chǎn)生的軸向力最小[17]。

綜上所述，鉆孔主要以剪切作用為主，連續(xù)殼單元不能體現(xiàn)厚度方向的剪切應(yīng)力。本文應(yīng)用Fortran語(yǔ)言編寫VUMAT子程序，并在層與層之間加入Cohesive黏性單元，建立三維實(shí)體鉆削仿真模型。以主軸轉(zhuǎn)速、進(jìn)給量為變量設(shè)計(jì)正交試驗(yàn)對(duì)軸向力進(jìn)行研究，并建立軸向力預(yù)測(cè)模型與仿真結(jié)果進(jìn)行比較，計(jì)算預(yù)測(cè)模型的誤差范圍。

1 鉆削有限元模型建立

1.1 CFRP鉆削模型

鉆削刀具選擇硬質(zhì)合金麻花鉆，用SolidWorks建立直徑為6 mm的麻花鉆模型，麻花鉆的頂角為118°，麻花鉆材料為硬質(zhì)合金YG8，密度為14 500 kg/m3，彈性模量為640 GPa，泊松比為0.23。

樹脂基碳纖維復(fù)合材料層合板是由單向板按照具體的鋪層設(shè)計(jì)，利用樹脂膠黏結(jié)，再經(jīng)高溫固化而成。基體不僅是纖維之間載荷傳遞的載體，還可以起到增強(qiáng)層合板韌性的作用，碳纖維作為增強(qiáng)基，具有增強(qiáng)強(qiáng)度和承載作用。層合板工件的規(guī)格為25 mm×25 mm×2 mm，且每層厚度一致，其鋪層角度及順序?yàn)閇-45°/90°/45°/0°/0°/45°/90°/-45°]，應(yīng)用Abaqus/CAE有限元仿真軟件建立鉆削模型，如圖1所示。

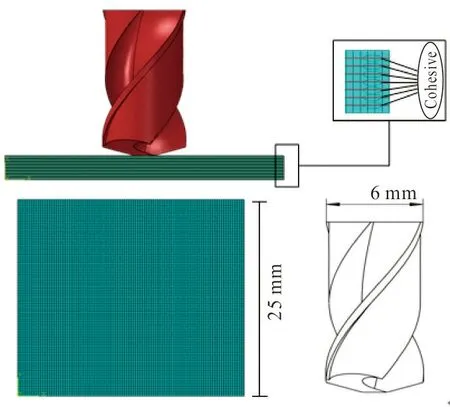
圖1 CFRP鉆削模型Fig.1 CFRP drilling model

樹脂基碳纖維復(fù)合材料層合板T700性能參數(shù)見表1。

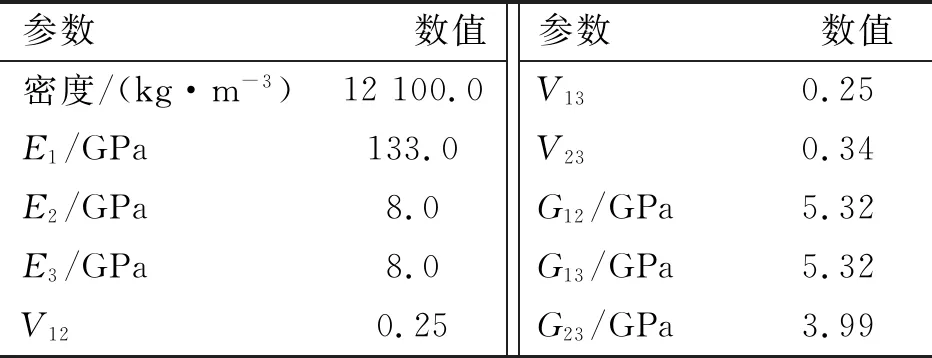
表1 層合板T700性能參數(shù)Tab.1 Performance parameters of laminated plate T700

為2，碳纖維層合板的厚度方向定義為3。

仿真模型中Cohesive材料參數(shù)見表2[18]。

表2 Cohesive材料參數(shù)Tab.2 Material parameters of Cohesive

1.2 模型定義與網(wǎng)格劃分

為了模擬實(shí)際的鉆削實(shí)驗(yàn)條件，將工件完全固定即限制工件的6個(gè)自由度，鉆削刀具因其材料各向同性的屬性，定義為剛體，并選取軸線方向上的參考點(diǎn)賦予轉(zhuǎn)速和進(jìn)給量。正確的網(wǎng)格單元類型和合適的網(wǎng)格單元?jiǎng)澐质荂FRP鉆削模型計(jì)算精確、收斂的前提[19]。CFRP工件采用自下而上的掃掠方式進(jìn)行劃分，賦予工件八節(jié)點(diǎn)減縮積分三維實(shí)體單元(C3D8R)，過(guò)渡層采用八節(jié)點(diǎn)三維黏性單元(COH3D8)，鉆削刀具設(shè)置為四節(jié)點(diǎn)線性四面體單元(C3D4)。鉆削刀具與CFRP工件之間的摩擦系數(shù)設(shè)置為0.3[20]。

1.3 Hashin損傷準(zhǔn)則

基于碳纖維復(fù)合材料各向異性的屬性和仿真實(shí)驗(yàn)，應(yīng)用Hashin失效準(zhǔn)則作為材料的失效判據(jù)。Hashin準(zhǔn)則包括纖維體的拉伸屈服、纖維體的壓縮屈服、基體在橫向拉伸和剪切下的屈服、基體在橫向壓縮和剪切下的屈服等4種失效形式[21-22]，

1) 纖維體拉伸屈服(σ11≥0)

(1)

2) 纖維體壓縮屈服(σ11<0)

(2)

3) 基體拉伸屈服(σ22+σ33≥0)

(3)

4)基體壓縮屈服(σ22+σ33<0)

(4)

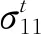
2 仿真試驗(yàn)

2.1 仿真試驗(yàn)設(shè)計(jì)

CFRP鉆削產(chǎn)生的軸向力受眾多因素影響，例如不同的轉(zhuǎn)速、進(jìn)給量都會(huì)造成軸向鉆削力大小的改變。因此選取主軸轉(zhuǎn)速n和進(jìn)給量f為變量，主軸轉(zhuǎn)速選取4個(gè)因素水平，進(jìn)給量選取3個(gè)因素水平。以CFRP鉆削仿真模型為基礎(chǔ)，主軸轉(zhuǎn)速、進(jìn)給量為變量建立多水平因素的試驗(yàn)方案，見表3所示。

表3 試驗(yàn)設(shè)計(jì)及結(jié)果Tab.3 Experimental design and results

2.2 仿真結(jié)果分析

軸向鉆削力主要來(lái)源于鉆削刀具與工件之間的摩擦力和材料本身的抗剪切力[23]，鉆削過(guò)程分為4個(gè)階段，鉆削階段如圖2所示。除去材料本身特性，加工參數(shù)的選擇對(duì)軸向鉆削力的影響也很大，不合理的加工參數(shù)可能導(dǎo)致工件質(zhì)量不達(dá)標(biāo)。因此合理的加工參數(shù)對(duì)鉆削質(zhì)量很關(guān)鍵。

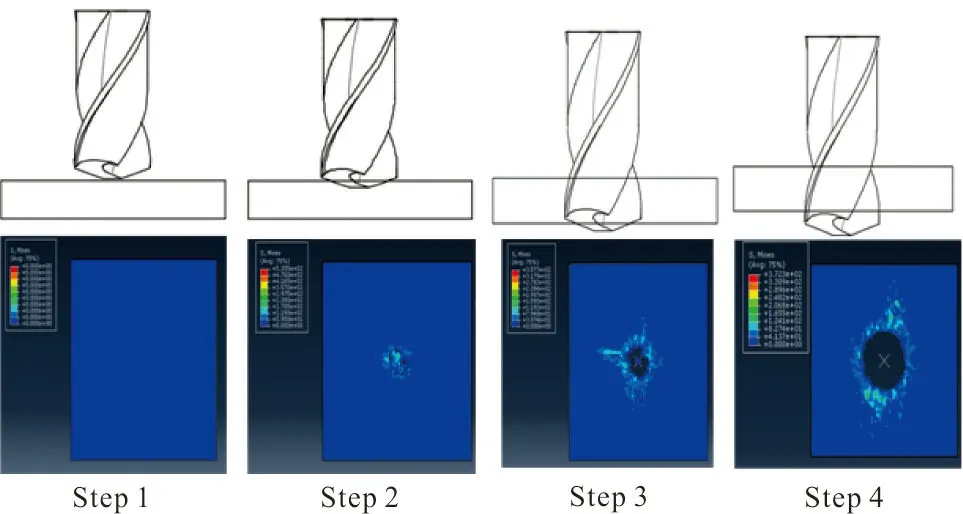
圖2 鉆削階段Fig.2 CFRP drilling stage

2.2.1 主軸轉(zhuǎn)速對(duì)軸向力的影響 選取1 000、2 000、3 000和4 000 r/min，4種因素水平作為仿真變量，通過(guò)仿真得到相對(duì)應(yīng)的試驗(yàn)結(jié)果。將試驗(yàn)結(jié)果與其相對(duì)應(yīng)的主軸轉(zhuǎn)速變量進(jìn)行處理得到主軸轉(zhuǎn)速與軸向力之間的變化規(guī)律如圖3所示。

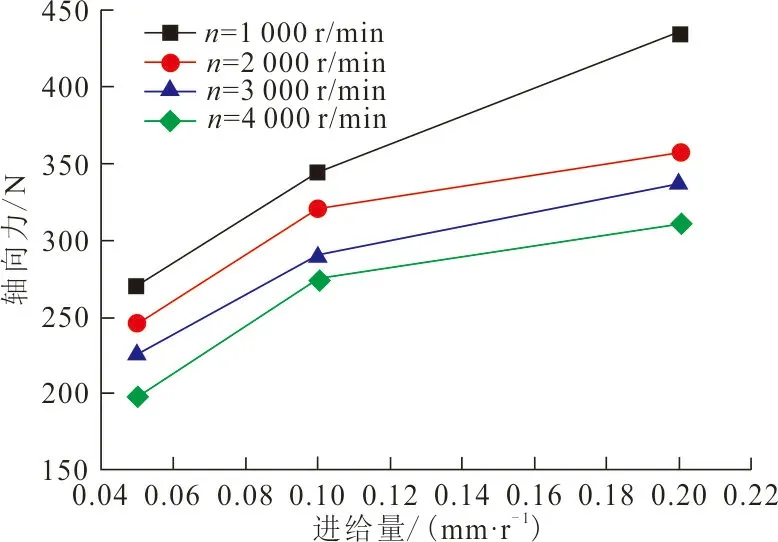
圖3 進(jìn)給量、主軸轉(zhuǎn)速對(duì)軸向力的影響Fig.3 Influence of feed rate and spindle speed on trust force

從圖3可以看出，在進(jìn)給量不變的情況下軸向力隨著主軸轉(zhuǎn)速的增大而減小。

2.2.2 進(jìn)給量對(duì)軸向力的影響 選取0.05 mm/r、0.10 mm/r和0.20 mm/r，3種因素水平作為仿真變量。通過(guò)仿真，得到相對(duì)應(yīng)的試驗(yàn)結(jié)果。并將試驗(yàn)結(jié)果與其相對(duì)應(yīng)的進(jìn)給量變量進(jìn)行處理得到相對(duì)應(yīng)的變化情況如圖3所示。可以得出，在主軸轉(zhuǎn)速不變的情況下，軸向力隨著進(jìn)給量的增大而增大。并通過(guò)與已發(fā)表的相關(guān)文獻(xiàn)[11]比較可以發(fā)現(xiàn)，本文仿真得到的加工參數(shù)與鉆削軸向力之間的變化規(guī)律，符合實(shí)際的CFRP鉆削規(guī)律。

極差分析見表4，從表4可以看出，對(duì)主軸轉(zhuǎn)速、進(jìn)給量進(jìn)行極差分析，可以得到進(jìn)給量對(duì)軸向力的影響最顯著，主軸轉(zhuǎn)速對(duì)軸向力的影響次之。方差分析見表5，從表5可以看出，進(jìn)給量的方差值大于主軸轉(zhuǎn)速方差值，即軸向力受進(jìn)給量的影響較大，受主軸轉(zhuǎn)速影響次之，該方差分析結(jié)果與極差分析結(jié)果一致。

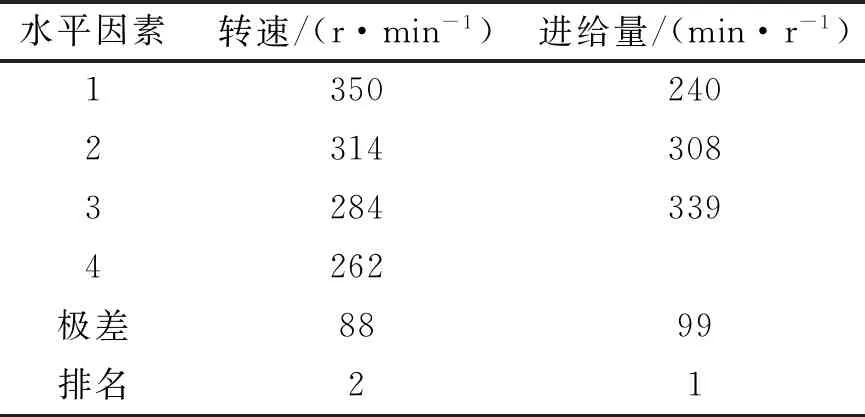
表4 工藝參數(shù)極差分析Tab.4 Analysis of extreme differences in process parameters

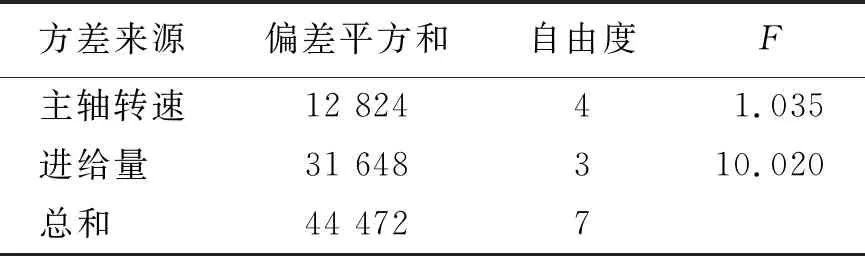
表5 工藝參數(shù)方差分析Tab.5 ANOVA of process parameters

3 軸向力預(yù)測(cè)模型建立

3.1 多元線性回歸模型

多元線性回歸方法是利用最小二乘函數(shù)對(duì)多個(gè)自變量進(jìn)行建模的回歸分析方法。用來(lái)研究一個(gè)應(yīng)變量依賴多個(gè)自變量的變化關(guān)系，廣泛的應(yīng)用于經(jīng)濟(jì)學(xué)、工程、醫(yī)學(xué)等領(lǐng)域[24]。

對(duì)仿真結(jié)果與加工參數(shù)進(jìn)行分析，建立多元線性回歸模型如公式(5)所示：

Fz=a0+a1x1+a2x2+ε

(5)

式中：Fz為軸向力;ai為常數(shù)項(xiàng);ε為誤差項(xiàng)。

通過(guò)對(duì)軸向力與主軸轉(zhuǎn)速、進(jìn)給量進(jìn)行回歸分析得到的軸向力預(yù)測(cè)模型方程如公式(6)所示：

Fz=280.92-0.03n+790.71f

(6)

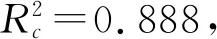
3.2 二次多元回歸模型

將主軸轉(zhuǎn)速、進(jìn)給量作為自變量，軸向力作為因變量，建立二次多元回歸模型，即

b5x1x2+ε

(7)

式中：Fz為軸向力；bi為常數(shù)項(xiàng)；ε為誤差項(xiàng)。

將仿真實(shí)驗(yàn)結(jié)果代入式(7)得到二次多元回歸軸向力預(yù)測(cè)方程，即

Fz=195.92-0.04n+2 656.43f+4.810-6n2+6 200f2+0.11nf

(8)

3.3 軸向力預(yù)測(cè)精度分析

多元線性回歸模型、二次多元回歸模型得到的預(yù)測(cè)值與試驗(yàn)值對(duì)比結(jié)果如圖4所示。

圖4 軸向力試驗(yàn)值與預(yù)測(cè)值的對(duì)比結(jié)果Fig.4 Comparison of the experimental and predicted values of the trust force

從圖4可以看出，多元線性回歸模型得到的預(yù)測(cè)值與試驗(yàn)值之間的最大誤差為11.3%，二次多元回歸模型得到的預(yù)測(cè)值與試驗(yàn)值之間的最大誤差為4.8%，二次多元回歸模型的鉆削軸向力預(yù)測(cè)精度較高，可以更好地將加工參數(shù)與軸向力之間復(fù)雜的信息關(guān)系體現(xiàn)出來(lái)。

4 結(jié) 論

1) 通過(guò)建立三維實(shí)體CFRP鉆削仿真模型，分析得到軸向力受進(jìn)給量影響最顯著，受主軸轉(zhuǎn)速影響最小，并且增大主軸轉(zhuǎn)速可以降低鉆削產(chǎn)生的軸向力。反之，增大進(jìn)給量則會(huì)使軸向力增大。

2) 通過(guò)回歸分析建立2種軸向力預(yù)測(cè)模型，多元線性回歸預(yù)測(cè)模型的最大相對(duì)誤差為11.3%，二次多元回歸預(yù)測(cè)模型的最大相對(duì)誤差為4.8%。二次多元回歸預(yù)測(cè)模型的預(yù)測(cè)精度明顯高于多元線性回歸預(yù)測(cè)模型，預(yù)測(cè)鉆削軸向力精確。