深海Spar平臺系泊系統動態張力影響因素分析*

武昌旭 魏代鋒 范 贊 張 進 潘 銳 劉軍鵬

(1.中國石油大學(北京)安全與海洋工程學院 2.中國船舶集團公司昆明船舶設備研究試驗中心 3.海洋石油工程股份有限公司)

0 引 言

隨著海洋工程的發展，人類對海洋資源的開發逐漸邁向深海領域。為了滿足需求，涌現出大量新興的海上浮式結構物，其中最具代表性的就是深海鉆井平臺和采油平臺。在深海平臺作業過程中，平臺通過系泊系統與海底相連來抵抗風、浪、流作用以及限制其運動[1]，系泊系統性能直接關系到平臺定位的準確性，而張力是評估深海系泊系統結構安全穩定性的關鍵指標。

目前，大多數深海Spar平臺系泊系統主要分單組分與多組分兩種[2]，其中單組分系泊系統由全錨鏈組成，多組分系泊系統一般為錨鏈-鋼纜-錨鏈和錨鏈-尼龍纜-錨鏈兩種結構組成形式。全錨鏈系泊系統結構單一、制造簡單，但由于其自重過大，多用于水深1 000 m左右的情況；相對于前者，多組分系泊系統對浮動設施承載能力造成的損失大大減小，得到了更廣泛的應用，但其結構的不同會增加設計的復雜性，因此研究系泊系統性能隨本身各組分以及環境變化而變化的規律具有很大的實用價值。

很多學者對系泊系統的靜態張力及構形計算開展了理論及試驗分析，在理論計算方面主要采用懸鏈線法。郝春玲等[1]提出了水流作用下錨鏈靜力分析的一種數值計算方法，通過計算得到了錨鏈頂端位移與錨鏈頂端應力呈非線性關系的結論。侯建軍等[3]分別給出了船體運動比較平緩、大風浪和走錨3種錨泊狀態下求解錨鏈對船體作用力的方法，為實現完整的錨泊仿真系統奠定了重要的理論基礎。R.J.SMITH等[4]使用改進的拉格朗日迭代法求解了系泊系統懸鏈線方程，該方法計算結果更為準確。CHAI Y.T.等[5]提出了一種半解析準靜態公式，用于解決部分觸地和完全懸掛的多腿系泊系統張力計算問題。余龍等[6]研究了多組分系泊纜在特定水深下的力學行為，并提出一個優化模型用于確定合適的系纜參數。

深海系泊系統在對平臺進行系泊定位時，兩者之間存在強烈的非線性作用，并且該作用會對系纜的性能和使用壽命產生重要影響，因此分析其在激勵下的動態響應也非常必要。唐友剛等[7]采用三維集中質量法建立深海系纜模型，計算系纜的構形及張力，根據各點的初始條件和位移邊界條件，求解了系纜的三維運動方程。朱忠顯等[8]基于集中質量法建立錨泊系統的動力學模型，并采用四階龍格-庫塔法進行了數值解算，對解算過程進行了優化。趙晶瑞等[9]考慮環境影響因素，依據集中質量法建立系泊纜繩柔性力學模型，對比研究了海流速度和波浪等因素對纜繩動態張力與水中構形的影響程度。CHAI Y.T.等[10]采用集總參數法將彎矩、扭矩及與海底的接觸等因素加入到海洋纜索的計算模型中，研究了不同工況下纜索的運動性能。A.TAHAR等[11]采用細長桿模型，對聚酯纜進行建模并與深海平臺進行了耦合動力分析。

上述研究主要針對系泊系統的靜態以及動態行為，主要分析對象為單組分系泊系統，缺乏對多組分系泊系統的相關研究，并且沒有分析多組分系泊系統性能與各影響因素之間的關系。鑒于此，本文首先通過改變相關參數，建立了OrcaFlex軟件中深海Spar平臺錨鏈單組分以及錨鏈-鋼纜-錨鏈多組分系泊系統模型；接著通過懸鏈線法對兩種系泊系統的靜態張力和構形進行了理論計算及對比；最后對深海Spar平臺施加正弦位移激勵，基于集中質量法并利用OrcaFlex軟件，改變鋼纜長度、激勵幅值以及激勵頻率，對系泊系統構形(系泊纜空間分布形態)和動態張力響應等進行參數敏感性分析，得出各參數對系泊系統性能的影響規律，計算結果對于實際工程中系泊系統的性能優化具有一定的指導作用。

1 靜態分析

對系泊系統進行整體靜態分析是為了得到其在頂部預張力、自身重力及浮力等作用下的初始平衡狀態，通過靜態分析可以得到系泊系統靜態構形以及系泊纜在靜態載荷下的應力分布情況，為動態分析提供初始條件。

1.1 懸鏈線方程建立

懸鏈線是指兩端固定，在重力作用下所形成的曲線，并且該曲線質量分布均勻、半徑一致、無延伸。當系泊纜的長度和深度比為2～3(與本文模型參數一致)時，系泊纜的重力遠大于其所受的海流載荷，在此情況下可以假設系泊纜不發生彈性變形，并采用懸鏈線方程來計算系泊系統靜態構形以及應力分布。根據懸鏈線理論，可以得到系纜上某一點的位置方程：

(1)

(2)

式中：x、z分別為系纜上某點到系泊系統頂端的水平距離和垂直距離，m；Hf為系纜某點應力的水平分量，kN；θt為系纜頂端點與水平方向的夾角，(°)；θb為系纜上某點與水平方向的夾角，(°)；M為系纜所受總重力，kN。

系纜所受各應力之間關系為：

Vf=Hftanθt

(3)

(4)

式中：Vf為系纜某點應力的豎直分量，kN；m為單位長度系纜質量，kg/m；s為系纜長度，m；g為重力加速度，m/s2。

1.2 系泊系統靜態張力、構形求解

本文的研究對象為美國Texas A & M大學[12]研究中心的一座Spar海洋平臺。平臺結構的主視圖與俯視圖分別如圖1和圖2所示。

1—Spar平臺；2—系纜3；3—系纜1。

1—系纜1；2—系纜2；3—Spar平臺；4—系纜3；5—系纜4。

文中每一根系纜代表實際情況中的一組，每組3根，系泊為半張緊方式，所采用的系泊系統為單組分系泊系統。單根系纜等效后，其物理及環境參數具體如下：系泊纜總長2 000 m，等效直徑0.415 m，單位長度質量961.2 kg/m，水深1 018 m，本文選取系纜1進行相關分析。

該平臺的其余主要技術參數如下：主體直徑40.54 m，高度216.40 m，質量2.592×108kg，吃水深度198.12 m。

本文采用錨鏈-鋼纜-錨鏈結構的多組分系泊系統，系統結構如圖3所示。

1—錨鏈；2—鋼纜；3—臥地錨鏈。

系泊系統總長仍為2 000 m，與平臺連接錨鏈長100 m，鋼纜長1 150 m，結合單組分系泊系統參數，計算得到多組分系泊系統參數，結果如表1所示[13]。

表1 多組分系泊系統等效具體參數Table 1 Parameters of multi-component mooring system

對單組分系泊系統頂端施加與水平方向夾角為67.6°、大小為1.37×104kN的預張力，以系泊系統海底錨固點為纜長零點，計算系泊系統沿纜長的靜態張力分布以及構形。接著計算多組分系泊系統在保持相同頂端點與錨固點位置條件下，各個節點的坐標以及沿纜長的靜態張力分布，計算結果分別如圖4和圖5所示。

圖4 系泊系統構形計算結果對比Fig.4 Comparison of structure configurations of mooring system

圖5 系泊系統靜態張力計算結果對比Fig.5 Comparison of static tensions of mooring system

由圖4可知，在保證系泊系統頂端點與海底錨固點水平方向距離1 547 m以及水深1 018 m條件下，單組分系泊系統觸地點在水平方向492 m左右，而多組分系泊系統觸地點為400 m左右。這是因為相比于單組分系泊系統，多組分系泊系統自重大大減小。由圖5可知：兩者張力都為沿纜長單調遞增的趨勢，在纜長0～750 m，兩者張力增加趨勢大致相同；在纜長750～2 000 m之間，單組分系泊系統張力增加趨勢更大，且兩者張力均在纜長1 995 m(距離頂端點5 m)處達到最大。多組分系泊系統最大靜態張力為0.64×104kN，單組分系泊系統最大靜態張力為1.39×104kN，約為多組分系泊系統的2.2倍。

以上結果表明，在單組分和多組分系泊系統頂端點與海底錨固點位置相同的條件下，多組分系泊系統的臥地段錨鏈更短，沿系纜分布靜態張力更小，即為了使平臺保證在相同位置，需要施加給多組分系泊系統的預張力更小，并且其自重更小。因此在實際工程中，在滿足載荷要求的條件下，優先選擇多組分系泊系統來完成對深海Spar平臺的系泊定位。

2 動態分析

深海系泊系統在對Spar平臺進行系泊定位時，除了受到頂部預張力、自身重力和浮力等作用外，還會受到海洋環境中波浪和海流等載荷的作用，以及由于頂端平臺運動而產生的復雜非線性相互作用，如果不能對系泊系統進行準確的動態分析，會直接影響到平臺定位的準確性甚至造成安全事故，因此對其在動態時的力學性能影響因素展開分析非常必要。

2.1 模型建立

對Spar平臺上部鉆機架和甲板采用6DBuoy模型建模, 平臺浮式柱狀硬艙主體采用Shape模型中的Elastic Solid進行模擬, 因為Elastic Solid可以模擬障礙物, 從而模擬擋水面積。建好相應模型后設置其主體質量并下放至海水中。Spar平臺簡化3D模型如圖6所示。

1—鉆機架；2—鉆井甲板；3—生產甲板；4—浮式柱狀硬艙。

在對系泊系統進行動態分析時，除了要考慮自身所受重力、浮力以及頂部張力等靜態載荷外，軸向拉伸回復力、結構內阻尼力、附加水質量力、拖曳力以及海底接觸力等工程載荷對其動態性能造成的影響也不可忽略。在利用OrcaFlex進行動力學計算時，可以采用集中質量法[14]對系泊系統進行建模，并綜合考慮工程載荷對于系泊系統的影響。系泊系統集中質量法離散示意圖如圖7所示。

OrcaFlex在對系泊系統進行建模時，將系泊纜看作由n段微元段組成的結構，第一段的下端與錨固點相連，第n段的上端與海洋平臺相連。每個微元段被分為兩段，每個半段自身的屬性力以及與流體相關的力被集中在一起并分配給該段末端的節點；系纜自身的軸向拉伸回復力以及結構內阻尼力通過連接節點的無質量軸向彈簧和線性阻尼器來表達。Spar平臺與系纜連接后的3D模型如圖8所示。

圖7 系泊系統集中質量法離散示意圖Fig.7 Discrete schematic diagram of concentrated mass method for mooring system

圖8 Spar平臺與系纜連接后的3D模型Fig.8 3D schematic diagram of Spar platform connecting to mooring system

2.2 參數設置

在利用OrcaFlex軟件分析時，參考 Spar平臺所在海況進行參數設定，多組分系泊系統的參數如表1所示，另外取其法向和切向拖曳系數分別為0.1和1.5。OrcaFlex分析中海洋環境參數設置如下：海流表面速度1 m/s，海流方向0°，水深1 018 m，海水密度1 030 kg/m3，海床土體剛度1 350 kN/m3，土體抗剪強度梯度1.3 kPa/m。

針對OrcaFlex中海流速度的設定，本文基于微幅波理論來進行計算，假設海流速度隨水深方向遞減，且水平方向的速度不隨時間變化。具體海流速度沿水深的分布如表2所示。

表2 不同水深的海流速度數值Table 2 Ocean current velocity in different water depths

深海Spar平臺在海風和波流的聯合作用下，往往會產生較大的運動響應，通過接頭傳遞到系泊系統頂端，進而引起系泊纜的運動。這些運動響應能夠引起海上平臺6個方向自由度的運動，包括垂蕩、縱蕩、橫蕩、艏搖、縱搖和橫搖，如圖9所示。研究表明，在6個方向自由度的運動中，垂蕩對系泊系統自身動張力影響最大[15]，并且垂蕩運動幅度為1 m時，能夠引起位于1 000 m水深的系泊系統觸地點水平移動10 m。因此本文著重分析平臺在發生垂蕩運動，即升沉運動時系泊系統的張力性能。

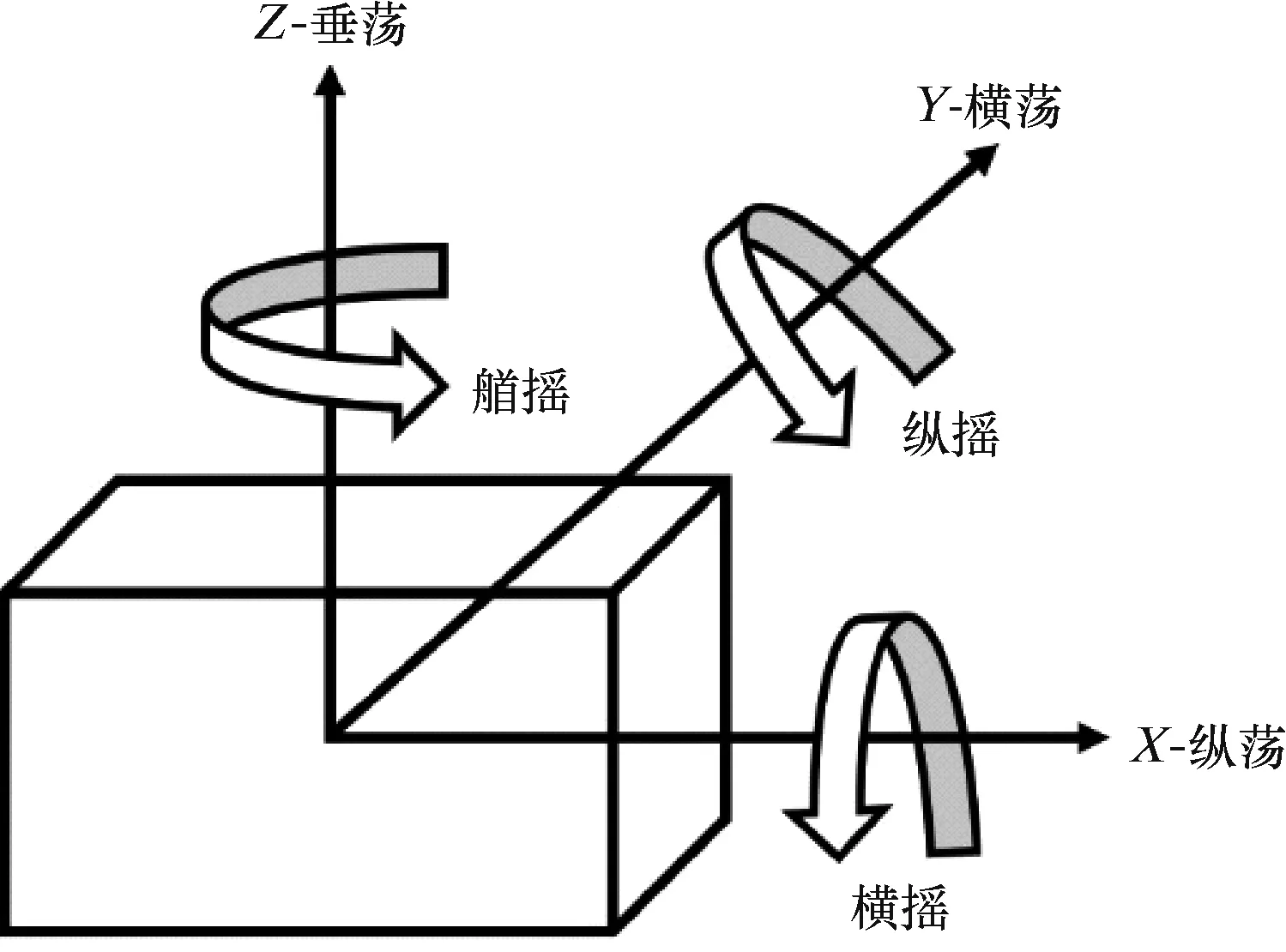
圖9 Spar平臺自由度示意圖Fig.9 Schematic diagram of Spar platform degrees of freedom

假定連接在系泊系統上的深海Spar平臺在波浪流的作用下做垂向簡諧運動：x(t)=Asin(ωt)，并將平臺運動作為邊界條件施加在系泊系統頂端。其中A為振幅，m；ω為頻率，rad/s。

定義L為錨鏈-鋼纜-臥地錨鏈3組分中鋼纜長度，單位為m。系泊纜總長與錨鏈長度分別保持2 000和100 m不變，臥地錨鏈長度隨鋼纜長度的變化而變化，分析鋼纜長度L、振幅A和頻率ω三者對于多組分系泊系統張力性能以及構形等的影響。

2.3 鋼纜長度影響分析

系泊系統的自重會隨著鋼纜長度的增加而減小，從而對浮動設施的承載能力造成的損失也減輕，但過長的鋼纜長度會增加系泊系統的安裝難度和成本，另外由于鋼纜過長，會更容易受到海洋內波流的影響，使其構形發生變化，影響系泊性能。圖10為保持頻率ω=0.6 rad/s不變，鋼纜長度L由950 m增至1 350 m(間隔為50 m)時系纜構形的計算結果。由圖10中A可知，鋼纜越長，系泊纜海底觸地點越靠前，且同一水平距離對應的系泊系統構形位置越靠上，接著不同鋼纜長度對應的系泊纜在水平方向950 m左右開始發生交匯，構形位置順序開始發生變化；由圖10中C可知，隨著鋼纜的增長，同一水平距離對應的系泊系統構形位置逐漸靠下，最終匯聚于同一上端點。

圖10 不同鋼纜長度下系泊纜構形示意圖Fig.10 Schematic diagram of mooring system configuration with different wire rope lengths

接著保持頻率ω=0.6 rad/s不變，取振幅A為3、5和7 m，分析計算不同鋼纜長度對應的系泊系統頂端張力。圖11、圖12和圖13分別為動態張力最值、動態張力幅值和動態張力平均值的結果示意圖。

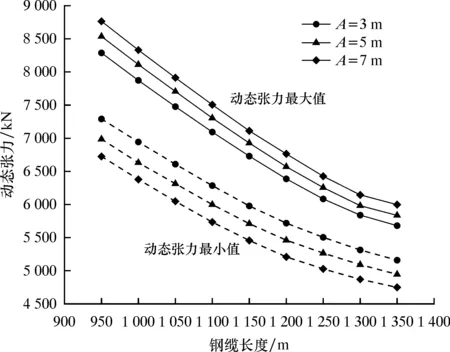
圖11 不同鋼纜長度下動態張力最大與最小值Fig.11 Maximum and minimum of dynamic tension with different wire rope lengths

圖12 不同鋼纜長度下動態張力幅值Fig.12 Dynamic tension amplitude with different wire rope lengths

圖13 不同鋼纜長度下動態張力平均值Fig.13 Schematic diagram of average dynamic tension with different wire rope lengths

由圖11和圖12可知，當鋼纜長度由950 m增至1 350 m時，系泊系統頂端對應的動態張力最大值與最小值也隨之減小，且對應的動態張力幅值也對應減小，說明鋼纜長度越長，系泊系統在相同激勵下的張力幅值越小，安全性也越高。

由圖13可知，隨著鋼纜長度的增加，系泊系統頂端的動態張力平均值與靜態張力值都發生了等幅減小，說明鋼纜長度的變化不會對其穩定性造成過大的影響。

2.4 激勵振幅影響分析

深海Spar平臺在遇到惡劣海況時，波浪振幅是反映海況惡劣程度最直接的參數，過大的振幅會造成海洋平臺失穩，產生安全隱患。本文假定深海Spar平臺在波浪流的作用下做垂向的簡諧運動，并將平臺升沉運動作為邊界條件施加在系泊系統的頂端，因此在分析波浪振幅的影響時，可直接將其作用在系泊系統頂端進行分析。

保持鋼纜長度1 150 m不變，取頻率ω為0.4、0.7和1.0 rad/s，激勵振幅由1 m增加至10 m(間隔為1 m)，分別計算不同振幅對應系泊系統頂端的動態張力最值、動態張力幅值和動態張力平均值，計算結果如圖14、圖15和圖16所示。

圖14 不同激勵振幅下動態張力最大值和最小值Fig.14 Maximum and minimum of dynamic tension with different excitation amplitudes

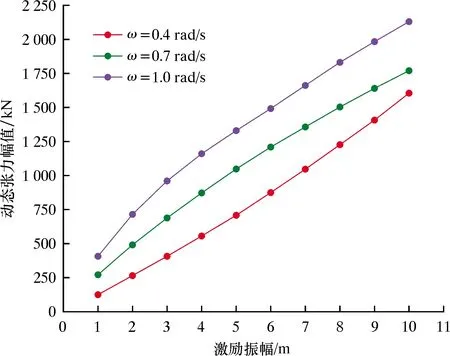
圖15 不同激勵振幅下動態張力幅值Fig.15 Amplitude of dynamic tension with different excitation amplitudes

圖16 不同激勵振幅下動態張力平均值Fig.16 Schematic diagram of average dynamic tension with different excitation amplitudes

由圖14和圖15可知，當激勵振幅由1 m增至10 m時，系泊系統頂端動態張力最大值隨之增大，張力最小值卻隨之減小，因此對應著動態張力幅值隨激勵振幅的增大而增大。

由圖16可知，由于鋼纜長度保持1 150 m不變，所以系泊系統頂端靜態張力值不隨振幅的變化而變化，但動態張力平均值卻隨著激勵振幅的增大而減小，其與靜態張力之間的差值也越來越大。由此可知，波浪振幅對于海洋平臺穩定性的影響較大，在惡劣海況下，過大的波浪振幅會使頂端動態張力幅值大大增加，對深海平臺系泊定位的安全準確性造成極大的威脅，因此在實際工程中對于系泊系統的設計制造，應著重考慮其在惡劣海況下的各項性能指標。

2.5 激勵頻率影響分析

隨機海浪理論認為，海面是由不同頻率組成的諧波疊加的結果，海浪在不同頻率上的能量分布就是海浪譜，不同頻率的海浪傳播速度不同，對深海平臺以及系泊系統的作用力也不同。保持波高A=3 m不變，取鋼纜長度L為1 100、1 150和1 200 m，激勵頻率ω由0.25 rad/s增加至1.00 rad/s(間隔為0.05 rad/s)，分別計算不同頻率對應系泊系統頂端的動態張力最值、動態張力幅值及動態張力平均值，計算結果如圖17、圖18和圖19所示。

圖17 不同激勵頻率下動態張力最大與最小值Fig.17 Maximum and minimum of dynamic tension with different excitation frequencies

圖18 不同激勵頻率下動態張力幅值Fig.18 Amplitude of dynamic tension with different excitation frequencies

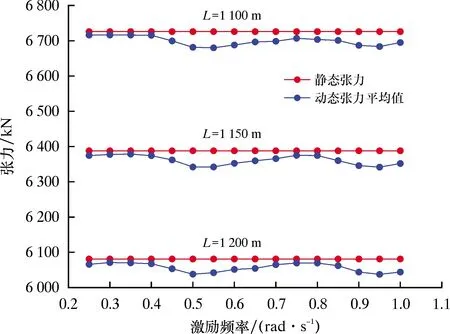
圖19 不同激勵頻率下動態張力平均值Fig.19 Schematic diagram of average dynamic tension with different excitation frequencies

由圖17可知：當激勵頻率ω由0.25 rad/s增加至1.00 rad/s時，系泊系統頂端動態張力最大值與最小值都表現出一種非線性變化規律，頂端動態張力最大值在激勵頻率為0.25～0.65 rad/s區間呈單調遞增的趨勢，在頻率為0.60 rad/s時出現峰值，隨后在0.95 rad/s時達到第二個峰值并在1.00 rad/s時達到最大值，其在激勵頻率變化區間總體呈增大趨勢；頂端動態張力最小值在激勵頻率變化區間總體呈減小的趨勢，并且其變化趨勢與張力最大值變化趨勢相反。動態張力幅值變化如圖18所示。由圖18可知：單組分系泊系統(L=0)的動態張力幅值在激勵頻率為0.55 rad/s時達到最大值；而多組分系泊系統的張力幅值總體呈增加趨勢，其變化趨勢與動態張力最大值變化趨勢基本一致，在激勵頻率為0.65 rad/s時出現峰值。這說明當激勵頻率小于0.80 rad/s時，動態張力最值及動態張力幅值在頻率為0.65 rad/s時均達到極值，深海平臺最為不穩定，對其本身的系泊定位與系泊系統的安全性造成的威脅最大。

由圖19可知，在激勵頻率變化過程中，3種鋼纜長度對應的系泊系統動態張力平均值與其本身靜態張力值相差不大，即動態張力最大值與最小值在隨激勵頻率變化過程中能關于系泊系統的靜態張力值基本對稱變化。

3 結 論

(1)在滿足深海平臺系泊定位要求的前提下，較單組分系泊系統而言，采用多組分系泊系統所需的預張力更小，在進行系泊定位時張力分布更均勻，更能保證系泊系統經濟有效地進行設計安裝。

(2)鋼纜長度的變化會引起多組分系泊系統重力的變化，進而引起構形的變化，系泊纜臥地錨鏈段長度隨著鋼纜長度的增加而減小。另外，動態張力最值、動態張力幅值以及張力平均值的變化都與鋼纜長度成反比關系，且鋼纜長度對系泊系統穩定性的影響不大。

(3)激勵振幅對深海平臺以及系泊系統穩定性的影響最大，動態張力最大值、最小值與激勵振幅分別成正比、反比關系，動態張力幅值隨激勵振幅的增大而增大，動態張力平均值與靜態張力值的差值隨激勵振幅的增大而增大，因此在實際工程中對于系泊系統的設計制造，應著重考慮其在惡劣海況下的各項性能指標。

(4)系泊系統的動態張力響應與激勵頻率之間存在一定的非線性關系，動態張力最大值、最小值與張力幅值均在激勵頻率0.60 rad/s附近出現了極值，且激勵頻率對系泊系統穩定性的影響比激勵振幅造成的影響小，因此在對多組分系泊系統進行性能評估時，應首先計算出導致其動態張力響應出現極值的頻率范圍，再對該頻率范圍內的各項性能進行評估，才能更好地保證其安全性。