鋼筋混凝土框架柱延性破壞準則研究

付 國，何 斌，劉伯權

(1. 西北農林科技大學水利與建筑工程學院，楊凌 712100；2. 長安大學建筑工程學院，西安 710061)

鋼筋混凝土柱是框架結構的主要承重構件，研究其抗震性能量化方法對提升結構整體性能、實現大震不倒設防目標、防止過早發生倒塌破壞具有重要意義。建立便于工程應用、符合性能退化規律和破壞現象的破壞準則，一直是抗震研究領域的熱點內容。近年來研究人員不斷完善與發展現有破壞準則，以提升破壞準則的適用范圍和精確度，取得了大量研究成果[1-6]。基于性能的抗震設計方法已經被工程界所認可，通過大量震害調查和試驗研究，細化了不同類型結構的變形量化限值[7]，變形準則、能量準則、Park-Ang 雙參數準則是破壞準則研究的主要方向和內容。

變形準則具有定義明確、測量方便的特性，且經受了大量的試驗驗證，我國抗震規范定義的位移角限值1/50 是留有足夠安全儲備的[8]，其本質上是結構不倒塌的標準而非倒塌標準。能量準則通過對比地震動輸入能量和結構所能提供能量大小，可較好地定義構件破壞，但耗能劃分和計算仍是研究的重點和難點問題。Park-Ang 雙參數準則[9-10]選取變形和耗能的組合定義柱的破壞，反映了首超破壞和累積損傷的影響，變形、耗能對結構破壞的貢獻大小及耦合作用仍需大量深入的量化研究。劉伯權[11]研究了等位移幅值加載下混凝土柱的低周疲勞特性，提出了等效延性破壞準則，但在準則應用和計算精度上仍需更多研究。

本文研究鋼筋混凝土柱破壞現象、承載力退化和延性變化規律，考慮變形能力強弱對柱破壞的影響，提出一種改進的延性破壞準則。對柱低周反復加載和單調加載試驗數據進行分析，考查延性破壞準則對構件破壞評估的有效性。

1 破壞準則概述

破壞準則應從宏觀現象、承載力退化、變形增長、滯回耗能等方面解釋性能退化規律和破壞機理，破壞指數計算需考慮變形、荷載、耗能等性能指標的影響，還應考慮加載制度、設計參數等因素的影響，同時兼具計算簡便、破壞標準合理等特性。

1.1 變形準則

變形準則定義結構破壞為變形值超過某一臨界狀態，具有概念清晰、判定標準唯一的優點，適用于單調、低周反復、地震動等加載方式。

混凝土柱變形能力的影響因素包括：1)配筋率、配箍率、混凝土強度等設計參數等；2)試驗方案中位移加載幅值、加載順序、軸壓比等；3)破壞過程中裂縫發育、保護層剝落、核心區破碎、縱筋箍筋失效類型等。不同混凝土柱的延性大小存在較大的差異，單一破壞標準很難反映構件破壞的差異性，甚至高估構件的變形能力和安全儲備。

針對美國太平洋地震中心(PEER)混凝土柱數據庫[12]的88 組矩形截面柱試驗數據進行分析，重點研究峰值點(對應最大荷載)和極限點(對應最大變形)的位移角變化規律。

圖1 是峰值點和極限點位移角的對比圖，絕大多數柱破壞時位移角超過了1/50 限值且留有一定安全儲備，但安全儲備的多少具有顯著差異。由圖2 中位移角限值與極限點、峰值點對比曲線可知，兩者沒有特定比例關系且多次相交，說明位移角為1/50 時，承載力退化、變形程度與構件最終破壞缺乏比例關系。單一位移角限值不能合理定義性能退化規律與程度，很難在兼顧安全與經濟的基礎上判定混凝土柱的破壞。

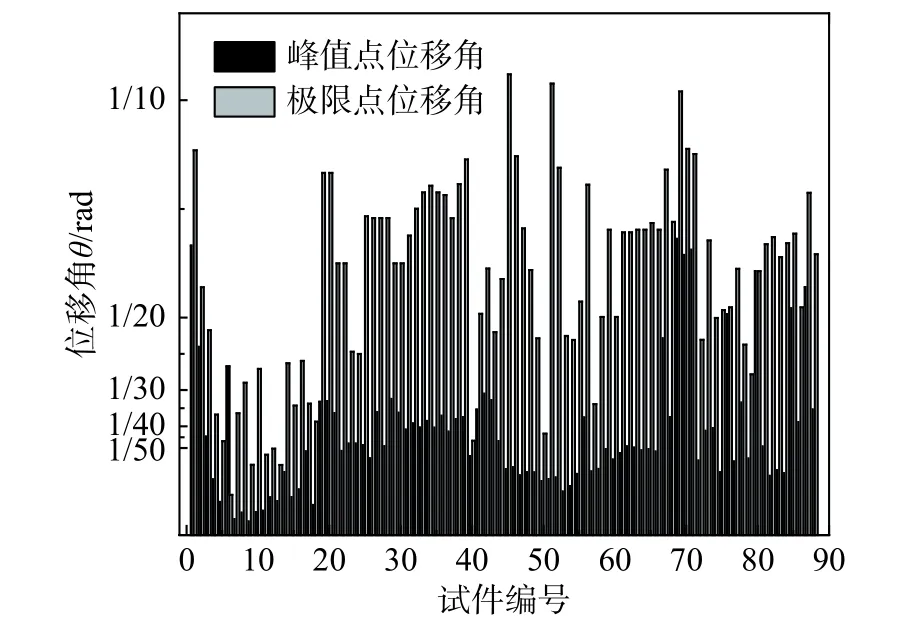
圖1 峰值點與極限點位移角對比Fig. 1 Comparison of displacement angle between maximum load and maximum deformation

圖2 1/50 位移角對應的變形與荷載曲線Fig. 2 Relationships between ultimate load and deformation of 1/50

圖3 是峰值點變形與極限點變形、極限點荷載與峰值點荷載的比例關系圖，混凝土柱的變形、荷載變化存在較大的差異，選擇變形、承載力退化或兩者組合的方式定義構件破壞仍有待深入開展。

圖3 承載力和變形的退化曲線Fig. 3 Degradation curve of load and deformation

1.2 能量準則

結構地震響應是一個能量輸入和耗散的過程，能量準則在理論上最為合理，由于混凝土保護層開裂、縱筋屈服、保護層初始剝落、混凝土保護層完全剝落、箍筋拉斷、縱筋屈曲和縱筋拉斷等破壞過程中的不確定性，破壞對應總能量的統計和分類工作復雜且不易確定[7]。

不同加載幅值和加載制度使得構件破壞和對應滯回耗能也存在較大差異，劉伯權[11]完成了相同設計參數的20 個框架柱擬靜力試驗，由表1 可知不同加載幅值和加載順序下構件破壞所需滯回耗能存在顯著差異甚至相差數十倍。隨加載幅值的增加單周滯回耗能值迅速增加，但構件破壞所需的總滯回耗能值卻顯著下降。

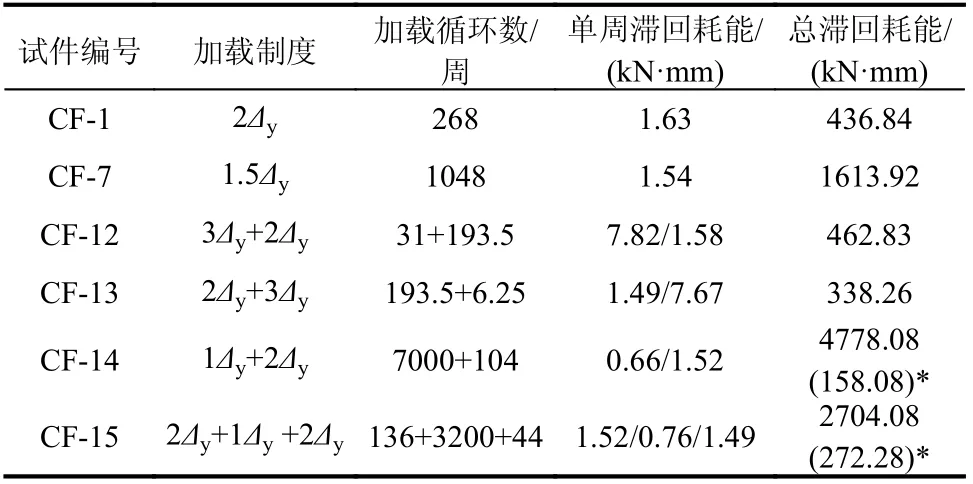
表1 鋼筋混凝土柱低周疲勞試驗參數[11]Table 1 Low-cycle fatigue experiment of RC columns

將能量劃分為彈性變形能、塑性變形能和損傷耗散能量三部分能夠更好定義破壞[13]，其中損傷耗能的累積最終引起結構破壞，確定各部分能量所占比例大小是破壞準則研究的重點和難點。文獻[14 - 16]探索了能量劃分的方法和依據：1)直接引起結構或構件破壞的部分耗能為有效耗能；2)其余能量不引起破壞或延緩破壞，如核心區已壓碎混凝土的研磨等，能量劃分方法、合理性驗證仍是后續研究的關鍵。

1.3 Park-Ang 雙參數準則

Park-Ang 雙參數破壞準則[9]定義結構破壞是由最大變形和累積耗能共同作用引起的。

Park-Ang 準則較好地考慮了首超破壞和累積耗能的影響，且破壞指數計算值與試驗結果吻合較好，其中組合參數β 和倒塌指數不為1 等是后續研究的主要方向[17-20]。

考慮變形增減與耗能增減之間的耦合關系，由剪跨比、軸壓比、縱筋配筋率、體積配箍率等參數組合得到的β 能否從理論上解釋變形與耗能對破壞的影響規律仍需深入研究。根據不同加載幅值的構件耗能特性引入有效耗能假設，改進的Park-Ang 準則可更好的定義結構破壞，耗能計算是影響破壞指數準確性的重要參數[14]。以表1 的2 組對比試驗為例(CF-12/CF-13、CF-14/CF-15)，同位移幅值加載下單周滯后耗能基本相同，總耗能大小甚至相差十余倍，考慮耗能的巨大差異與柱破壞之間關系仍需開展廣泛的試驗研究和數據驗算。

1.4 等效延性破壞準則

劉伯權[11]研究了框架柱的低周疲勞特性，提出包含延性大小和加載次數的等效延性破壞準則。

1)延性系數是柱塑性變形發育程度的量化指標，既反映變形的大小，也定義塑性變形發育程度的大小，較位移更適宜預測和評估構件破壞。

2)加載次數與加載幅值的組合反映了構件破壞的累積效應，加載次數越多、加載幅值越大，柱的破壞越嚴重。

3)延性準則適用于單調加載、低周反復加載、地震動加載三種不同的加載方式，實現了破壞準則形式上的統一。

2 延性破壞準則

2.1 延性準則計算式

根據已有試驗研究資料，對混凝土柱的部分破壞特性總結如下：

1)考慮地震動作用的時間相對較短且往復次數有限，混凝土柱位移加載幅值低于屈服位移時，構件幾乎不發生破壞，定義彈性范圍內即延性系數μ<1 時柱不破壞，對應破壞指數為0。

2)單調、低周反復等加載方式下單調加載位移值最大，可取單調加載下的混凝土柱極限位移為柱的最大延性系數μmax。μmax考慮了軸壓比、剪跨比、配筋率、混凝土強度等設計參數。

單調加載下柱的極限位移可由式(7)和式(8)計算得出[21]：

3)低周反復加載過程中位移幅值、加載次數對構件破壞的影響最為顯著，是破壞準則中必須包含的參數。抗震理論和試驗研究表明軸壓比和配箍率對構件破壞和性能退化有顯著影響。

綜上，通過試件的試驗數據計算研究，定義框架柱的延性破壞準則如下式所示：

2.2 參數定義與說明

小于屈服位移時 (μi-1)項為0，表示延性系數小于1 時柱不發生性能退化，隨著延性增加構件破壞程度也進一步加劇。延性系數項取2，主要基于改進Park-Ang 準則研究和耗能計算中揭示的耗能與延性系數存在近似平方關系[14]：1)破壞指數增加與延性增加是非線性的；2)變形與承載力存在對應關系，參考耗能計算方法定義延性系數與破壞指數為平方關系，延性準則計算結果也表明平方關系能夠較準確的定義混凝土柱破壞。

βi為相同位移加載幅值的循環次數，當循環次數小于3 時取實際循環數，循環次數大于3 時取βi=3。

軸壓比影響系數kn解釋了隨軸壓比增加構件破壞程度加劇的試驗現象，22n關系式由破壞指數計算數據擬合得出。前期擬合數據均為軸壓比0.2 的試件，系數取0.3 考慮n=0.2 時kn=1.019 ≈1.0。

配箍率影響系數kρv借鑒阿倫尼烏斯公式進行研究，由于混凝土柱低周反復加載試驗中直接研究配箍率影響規律的試驗較少，延性準則首先完成kρv=1.0 的計算研究。

需要指出的是μmax與kn計算式中均包含了軸壓比系數，μmax是混凝土柱在單調加載下的理論最大變形能力，與低周反復試驗無關；而kn是反復加載試驗過程中延性系數與柱破壞程度之間關系的系數，兩次軸壓比計算的適用范圍和目的不同。

3 延性破壞準則驗證

3.1 低周反復加載試驗驗證

為驗證延性破壞準則的合理性和準確性，首先對比了Park-Ang 準則[22]、改進Park-Ang 準則[14]與延性破壞準則的計算結果，并將全部加載循環對應的破壞指數進行對比，計算結果如表2 所示。

表2 破壞指數計算對比Table 2 Comparison of damage index

三種破壞準則對應的破壞指數平均值分別為1.408、1.084 和0.857，延性準則對應破壞指數最小，限于篇幅選取了試件Kzc4 和Kzb3，將Park-Ang 準則、改進Park-Ang 準則、延性準則計算結果分別繪成柱狀圖，如圖4 所示。

由圖4 可知延性系數為1 時，延性準則對應破壞指數為0，表明結構彈性階段幾乎不發生破壞；延性系數較小時，延性準則破壞指數顯著小于Park準則和改進Park 準則，小位移幅值加載下結構破壞程度輕微，與試驗現象更為吻合；接近破壞時延性準則對應破壞指數增加迅速，更好地解釋了位移加載幅值越大破壞程度越嚴重的試驗現象。

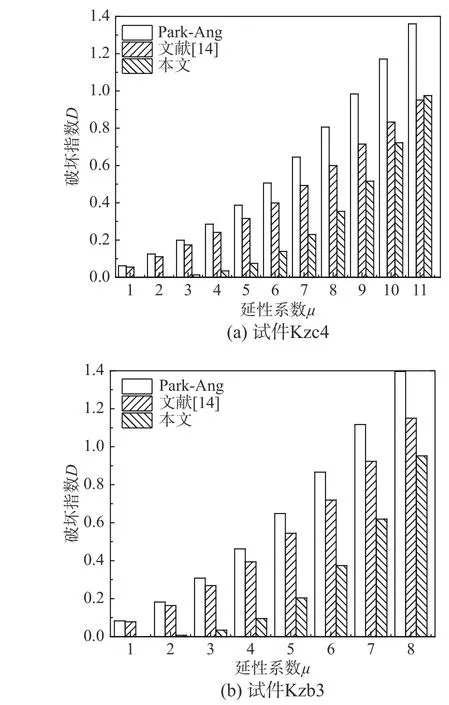
圖4 三種準則對應的破壞指數對比Fig. 4 Comparison of damage index base on three failure criterion

為驗證延性準則的合理性與準確性，選取日本Kawashima[23]數據庫部分混凝土柱以及國內混凝土柱試驗數據進行了計算和驗證，由于數據較多，所有試驗的詳細參數不詳細列出，文獻來源和編號見表3，計算結果見圖5。

圖5 混凝土柱反復加載破壞指數Fig. 5 Damage index of RC columns under cyclic loading

表3 混凝土柱試件文獻來源與編號Table 3 Literature sources and numbering of RC columns

105 組框架柱的破壞指數平均值為0.923，標準差為0.265，延性準則能夠很好地預測構件破壞。離散性偏大的一個主要原因是承載力退化大小不統一，以文獻[24]為例(破壞指數見圖6)，承載力退化至85%時破壞指數平均值為0.655，退化至40%為1.406，兩者相差超過1 倍。

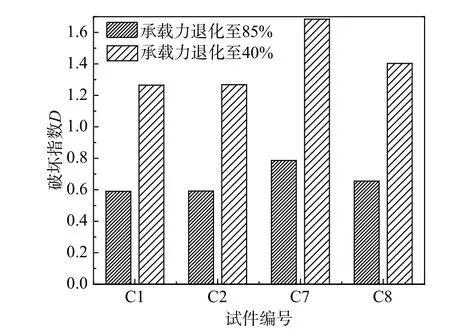
圖6 承載力退化至85%與40%時的破壞指數Fig. 6 Damage index of capacity degradation with 85% and 40%

根據各試件的承載力退化值，將已完成的105 組數據按照承載力退化程度重新進行了排序(承載力退化值優先由文獻得出，未明確給出的由滯回曲線得出)，得到退化程度為20%～30%、30%～40%、40%～50%、50%～60%、60%～70%、70%～80%、80%～90%共7 組破壞指數平均值，如圖7 實線所示。

對90%分組數據進行整理，李義柱[29]、劉金升[30]、錢稼茹[31]組試件按滯回曲線得到的承載力退化幅值分別為54.7%、37.0%、72.6%、60.6%、78.6%(數 據 由GetData 軟 件 描 點 得 出)，TP-15、TP-16 較TP-14 加[23]密區分別增長1 倍和2 倍，解詠平[26]組研究了構件的尺寸效應，對應2 組數據的加載循環數多，移除以上數據后90%分組包含了5 組試件，對應破壞指數平均值為0.631，調整后見圖7 虛線。鋼筋混凝土柱的承載力退化越嚴重，破壞指數越大，破壞程度越充分。

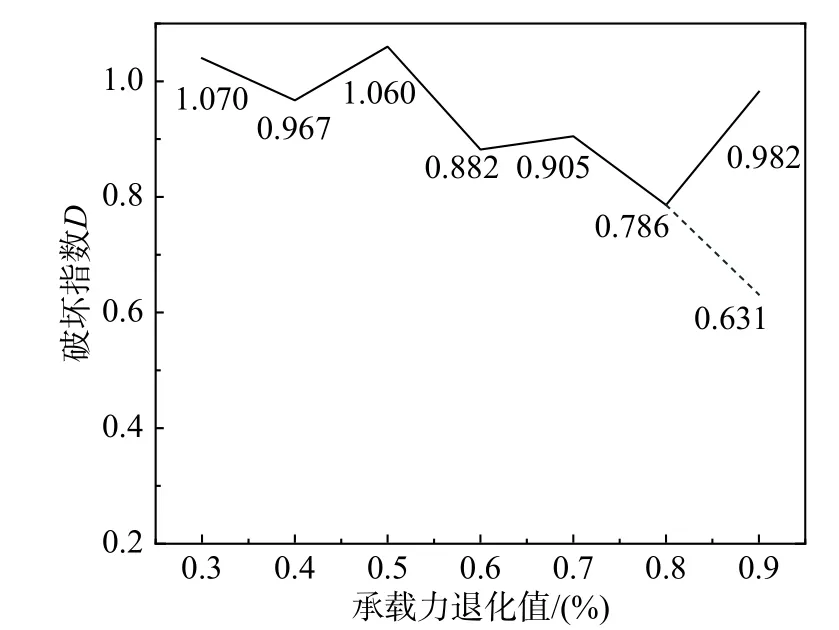
圖7 破壞指數與承載力退化關系圖Fig. 7 Relationship curves of capacity degradation and damage index

3.2 單調加載試驗驗證

把單調加載視為位移幅值為 Δmax、加載循環數為1/4 的滯回加載[11]，單調加載下(μi=μmax)的延性破壞準則計算式可改寫為：

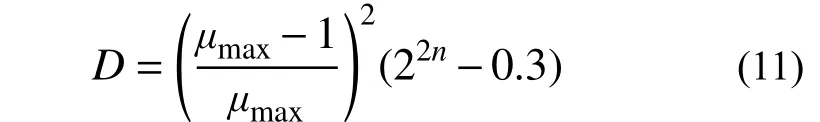
延性破壞準則將兩種加載方式對應的破壞指數計算統一到一個公式中，同時考慮了首超破壞和累積損傷破壞，反映了位移幅值和滯回循環對構件破壞的影響，對文獻[11, 25, 41]的單調加載試驗數據進行了分析，得到破壞指數如圖8 所示。

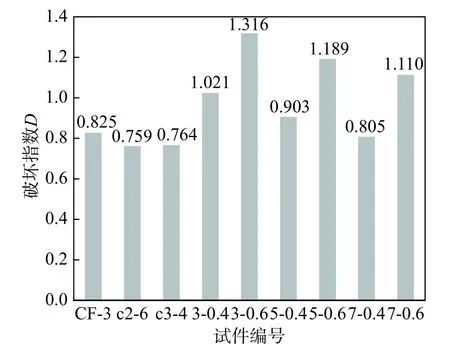
圖8 鋼筋混凝土柱單調加載破壞指數Fig. 8 Damage index of RC columns under monotonic loading

單調加載試驗破壞指數計算結果表明，9 組試件的平均值為0.966，標準差0.191，延性準則也可以較好地定義混凝土的首超破壞，解釋單調加載下構件的破壞規律。

4 考慮配箍率變化的延性破壞準則

4.1 配箍率影響系數

箍筋對增強核心區混凝土約束、抗震性能提升具有顯著影響，收集到的試驗數據中直接研究配箍率與破壞規律的數據較少，需要借鑒相關理論探索配箍率對構件破壞的影響。

阿倫尼烏斯公式是由瑞典的阿倫尼烏斯所創立的化學反應速率常數隨溫度變化關系的經驗公式：

式中：k為速率常數；R為摩爾氣體常量；T為熱力學溫度；Ea為表觀活化能；A為指前因子。研究表明阿倫尼烏斯公式計算值與試驗值吻合較好，在化學反應速率方面獲得了廣泛應用[42-43]。

如果把混凝土柱的破壞類比為化學反應，配箍率類比為溫度，混凝土柱的破壞過程也可用阿倫尼烏斯公式進行說明。常數Ea對應配箍率對構件性能提升的最小值， 1/ρv表明配箍率較低時ρv增加對柱的性能提升影響顯著，隨著配箍率增加對構件破壞的影響趨緩。

為降低試驗和文獻來源的誤差，將105 組數據按配箍率每隔0.1%劃分一組，包括0.5%～0.6%、0.6%～0.7%、···、2.2%～2.3%、2.3%～2.4%共15 組數據，刪除了數量過少或破壞指數顯著偏大的3 組數據，每組取平均值后得到散點圖如圖9所示。

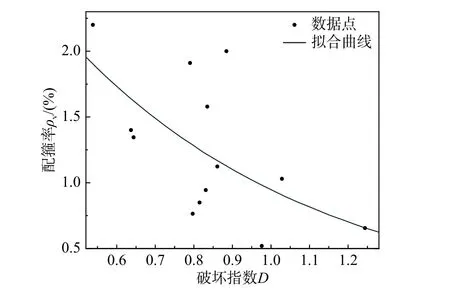
圖9 kρv 擬合曲線Fig.9Curvefittingof kρv

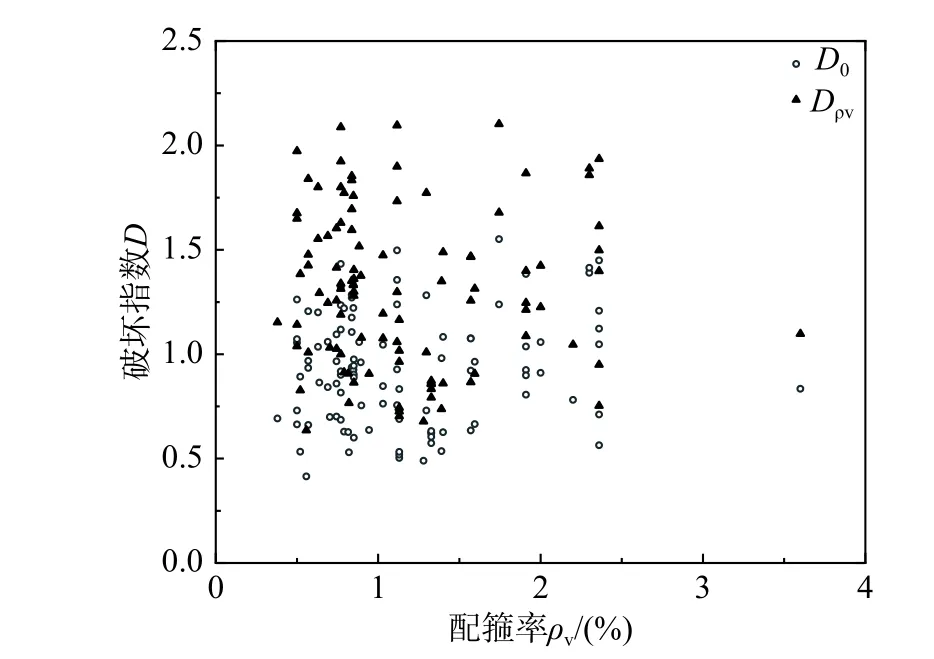
圖10 不同配箍率的混凝土柱破壞指數Fig. 10 The columns damage index in different stirrup ratio

4.2 改進后的延性準則計算研究

由于混凝土材料、加載制度、設計參數的差異性，且缺少柱破壞臨界狀態的統一標準，為說明改進后延性準則公式合理性，本文定義破壞指數隨承載力退化值線性減少，即：

式中：D0.85為承載力退化至峰值承載力85%時結構的破壞指數；d為承載力退化值。

D0組破壞指數和Dρv組破壞指數根據承載力退化程度調整為85%后分別對應為D0,0.85組數據和Dρv,0.85組數據，兩組破壞指數分布如圖11 所示，四組破壞指數的平均值和標準差見表4。

表4 框架柱反復加載試驗破壞指數Table 4 Statistical table of damage index under cyclic loading

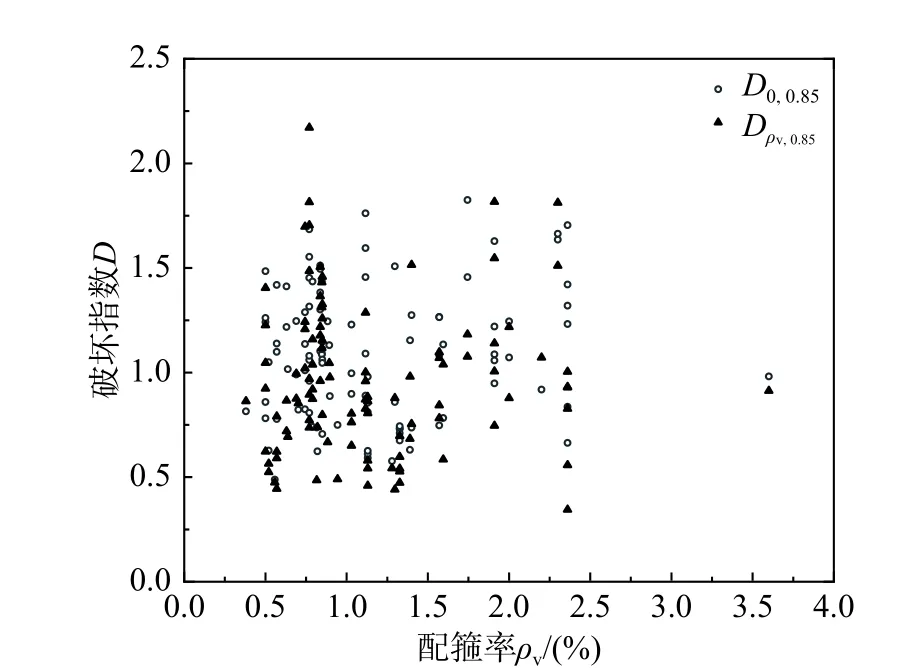
圖11 不同承載力退化程度的混凝土柱破壞指數Fig. 11 The columns damage index in different capacity degradation

D0組和Dρv組數據對比表明考慮配箍率影響后破壞指數平均值增大，但標準差增長較小，Dρv組數據能夠更好揭示構件破壞特性。D0,0.85組數據與D0組數據的平均值和標準差變化均較小，Dρv,0.85組數據考慮了承載力退化和配箍率影響，破壞指數的平均值最接近1.0，且標準差變化不大。

4.3 改進后的單調加載延性準則計算研究

類似的將9 組單調加載試驗對應的延性準則破壞指數也按四種情況分析，計算結果見表5。

表5 框架柱單調加載試驗破壞指數Table 5 Statistical table of damage index under monotonic loading

單調加載試驗結果中D0,0.85和Dρv,0.85數據標準差較大，原因是C3-4 和C2-6 試件破壞時承載力已退化至幅值承載力的33%，換算為承載力幅值85%時破壞指數顯著降低。計算表明延性準則也能定義單調加載下柱的破壞，實現了單調加載與反復加載破壞準則的統一。

5 混凝土柱性能標準

低周反復加載柱的破壞可劃分為4 個階段：輕微破壞對應混凝土裂縫發育階段(包括橫向裂縫、垂直裂縫、斜裂縫的生成與發展)；中等破壞對應保護層混凝土起皮剝落至大面積剝落；嚴重破壞對應核心區混凝土研磨、承載力大幅下降；失效/倒塌對應構件不能繼續抵御地震作用并退出工作。

將包含詳細試驗現象描述的9 組29 根框架柱破壞曲線繪于圖12 中，考慮試驗中位移幅值的增量基本相同，曲線斜率即為柱的破壞速率，加載幅值越大破壞指數越大，破壞速度也越快。

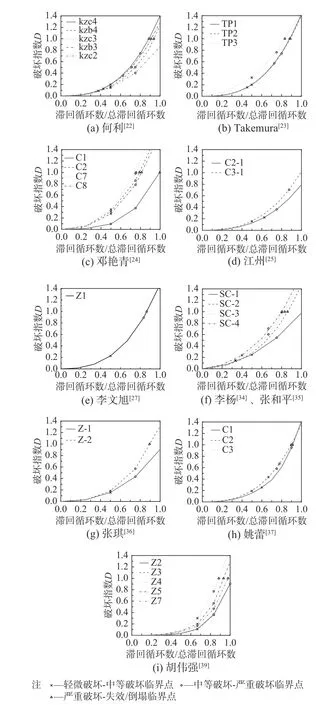
圖12 混凝土柱破壞曲線Fig. 12 Damage curves of columns

29 根框架柱的輕微-中等破壞臨界點、中等-嚴重破壞臨界點破壞指數見表6，平均值分別為0.21 和0.64。參考延性準則計算結果，建議失效或倒塌破壞標臨界值為1.0。

表6 混凝土柱破壞特征點Table 6 Damage feature point of RC columns

根據承載力退化值、延性準則計算結果，參考國內外學者給出的混凝土柱破壞標準和延性準則破壞指數統計結果，給出了鋼筋混凝土柱的延性準則評價標準，列于表7。

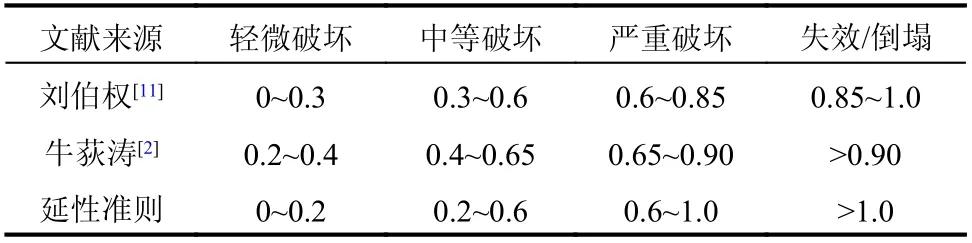
表7 延性準則破壞評價標準Table 7 Damage evaluating standards of ductility criterion

6 結論

本文對混凝土框架柱的變形能力與性能退化關系進行了研究，提出一種改進的混凝土柱延性破壞準則，結論如下：

(1)延性破壞準則考慮了變形能力強弱、軸壓比、配箍率對性能退化的影響規律，將反復加載與單調加載兩種加載方式組合到一個表達式中，能夠較好地定義混凝土柱破壞。

(2)完成了105 組混凝土柱反復加載數據計算，Dρv,0.85組對應破壞指數平均值為0.963，標準差為0.354；完成了9 組單調加載試驗數據計算，Dρv,0.85組破壞指數平均值為0.895，標準差為0.359。考慮配箍率影響和承載力退化幅值的Dρv,0.85組能夠更好地定義混凝土柱的破壞

(3)將混凝土柱性能退化劃分為4 個階段，給出了對應的破壞指數分布范圍，延性準則破壞評價標準與試驗破壞現象吻合較好，可用于柱的破壞評估和預測。