考慮車鉤垂向約束的機車軸重轉移計算方法研究

張志超，李 谷，儲高峰，祖宏林

(中國鐵道科學研究院集團有限公司機車車輛研究所，北京 100081)

機車牽引列車起動或運行時，作用于機車的輪周牽引力和車鉤力不在同一高度，會產生一個促使機車發生點頭運動的力矩，從而引起機車各軸軸重的重新分配。軸重轉移會影響機車黏著重量的利用和牽引力的發揮，減小機車軸重轉移是提高黏著利用率的重要措施[1-4]。目前為止，針對該問題已經開展了廣泛而深入的研究工作，得到了很多軸重轉移計算方法和公式[5-19]。這些計算方法大致可分為兩類：1)幾何關系推導法[1,5-13]，根據車體、構架、輪對的相對位置關系以及一系、二系變化關系，并結合力的平衡關系解析推導機車實際軸重轉移量；2)仿真計算分析法[14-18]，采用多體動力學分析軟件建立機車動力學分析模型，利用該模型計算機車牽引時的軸重轉移穩態值。幾何關系推導法往往針對特定車型進行公式推導和求解，表達式相對復雜，通用性較差，難以模擬車鉤高度、牽引點高度變化對軸重轉移的影響。仿真計算分析法雖然通過仿真分析能夠得到更為接近機車實際運行工況的軸重轉移特性，但是同樣存在通用性問題，不同類型機車需要重新建模，而且為了考慮電機對軸重轉移的影響需要建立詳細的電機系統模型。因此，為了實現高效快捷的機車軸重轉移計算以及牽引黏著特性設計，有必要建立具有通用性的機車軸重轉移計算方法。

另外，目前的機車軸重轉移計算分析只考慮了車鉤縱向牽引力的影響，并未考慮在縱向拉鉤力作用下連掛車鉤鉤頭接觸面對機車后端垂向運動的約束作用。這種簡化使得機車不受額外垂向作用力，因此車體基本沒有垂向位移，只會產生繞其質心的點頭轉動，如圖1(b)所示。此時雖然機車各軸間的軸重會發生轉移，但是各軸軸重總和保持不變。然而，機車實際牽引列車時，其后端連掛車鉤高達數百千牛的縱向拉鉤力會使得鉤頭接觸面產生垂向摩擦力，抑制車鉤及機車后部產生垂向位移，當該垂向位移被完全約束時，機車將產生如圖1(c)所示的以后端車鉤連掛點為中心的點頭轉動。此時機車車體運動形態的變化勢必帶來各軸軸重轉移的變化，并且各軸軸重總和也不再保持不變。連掛車鉤垂向約束作用的影響在以往各種機車軸重轉移計算方法中均未曾予以考慮，因此十分有必要明確它對軸重轉移的具體影響程度和規律。

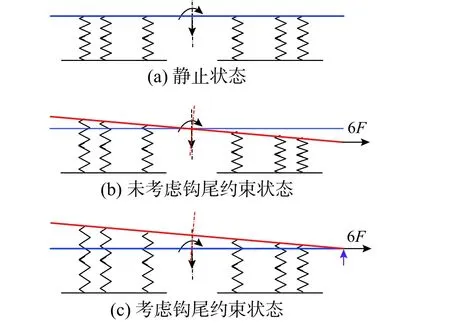
圖1 機車牽引時車體運動形態示意圖Fig. 1 Schematic diagram of locomotive carbody motion during traction

針對上述機車軸重轉移計算存在的兩個問題，本文將機車后端連掛車鉤的垂向約束作用等效為線性彈簧約束，通過等效約束剛度的大小來模擬后端車鉤垂向約束作用的強弱；并考慮牽引桿布置方式、牽引點高度變化的影響，通過機車受力平衡分析推導了機車軸重轉移計算公式，建立了具有通用格式的軸重轉移計算矩陣方程，為機車軸重轉移計算提供了具有統一性的新方法。在此基礎上，針對2(B0-B0)軸式機車分析了連掛車鉤垂向約束的影響規律，針對C0-C0 軸式六軸機車詳細分析了一系和二系彈簧剛度、牽引點高度等因素對軸重轉移的影響規律。

1 考慮車鉤垂向約束的機車軸重轉移計算方程

正如前文所述，連掛車鉤鉤頭垂向摩擦作用會對機車的軸重轉移產生影響，因此需要在分析模型中予以考慮。一般而言車鉤鉤頭的摩擦約束作用呈現非線性特性，并且車鉤本身相對車體還具有一定范圍的垂向自由轉動，難以在軸重轉移靜態計算中實現。為此，本文將其簡化等效為具有一定剛度的線性彈簧約束，通過改變等效約束剛度的大小來體現車鉤鉤頭垂向約束作用的強弱，如圖2 所示。

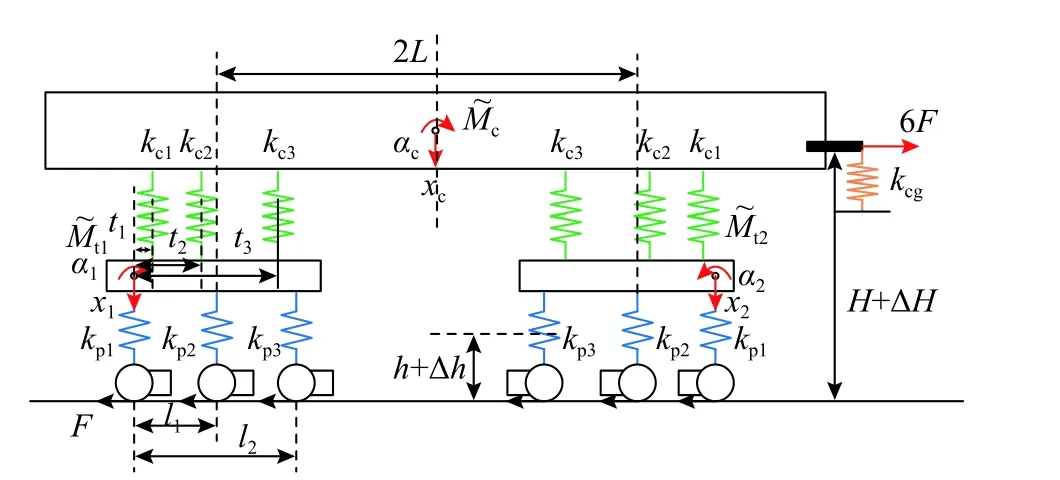
圖2 機車軸重轉移分析圖Fig. 2 Diagram of locomotive axle load transfer

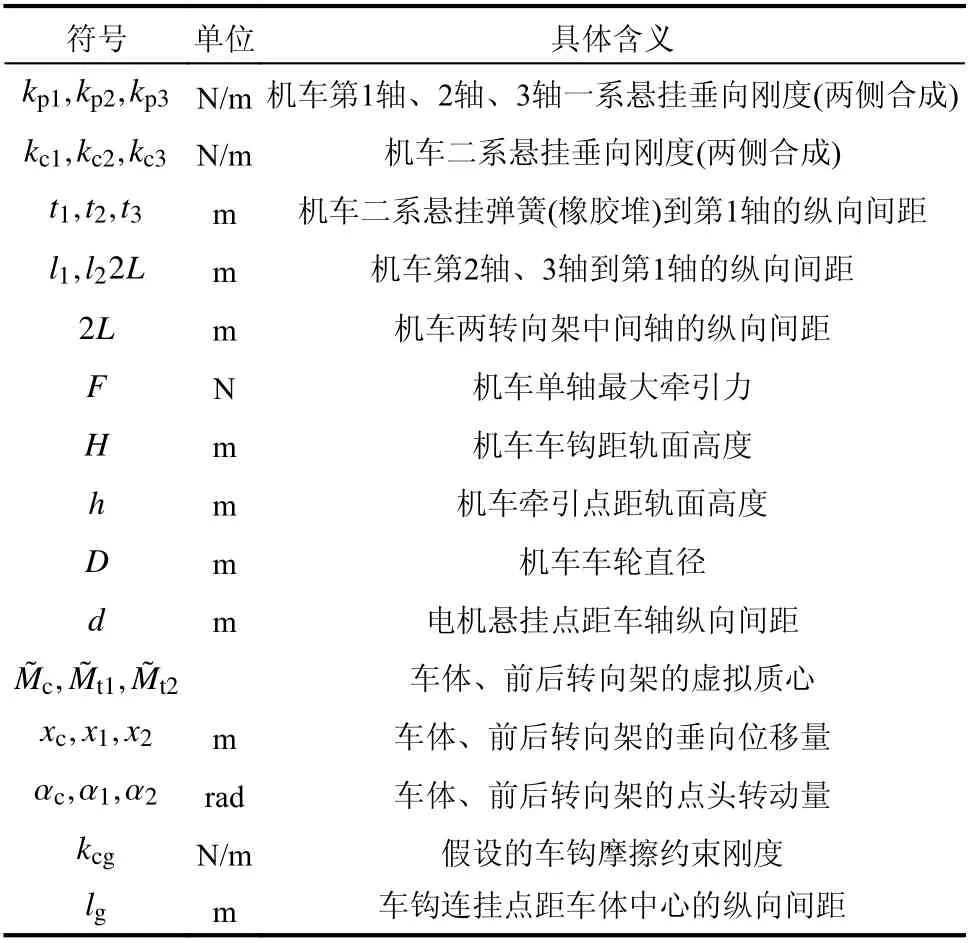
表1 各符號物理含義說明Table 1 Description of physical meanings of symbols

根據車體、前后轉向架的垂向力和力矩平衡關系，分別建立相應的平衡方程。車體垂向受力平衡方程：

前轉向架垂向力平衡方程：

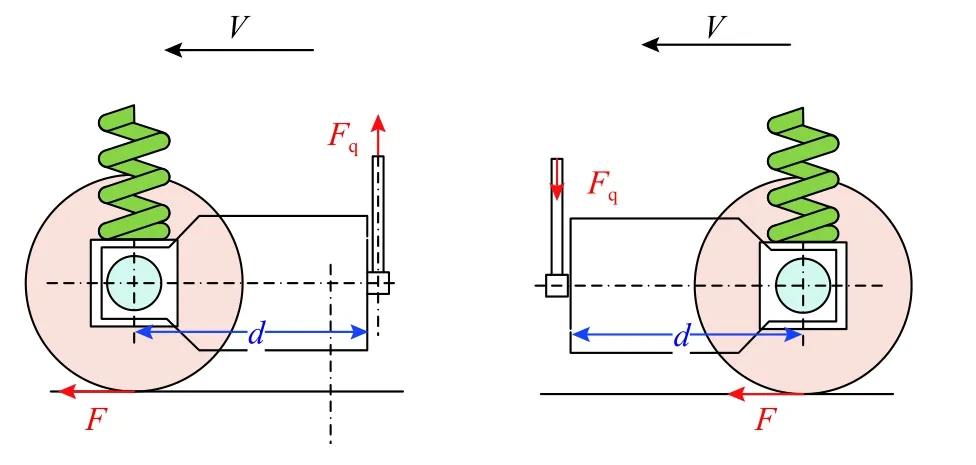
圖3 牽引電機布置位置示意圖Fig. 3 Diagram of traction motor arrangements

將式(1)～式(6)統一寫成矩陣形式，可得：

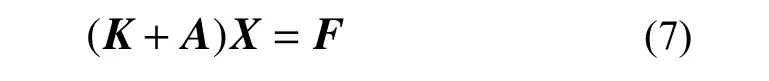
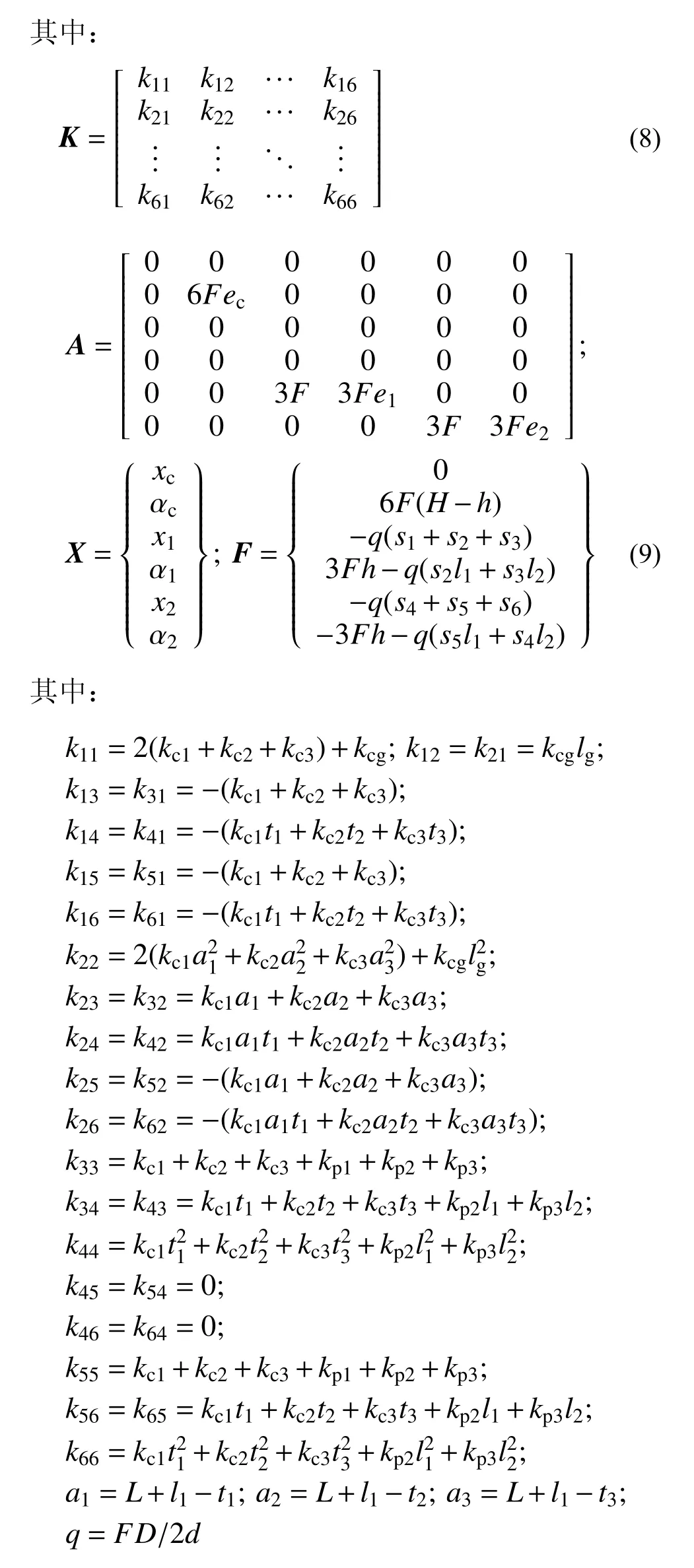
通過式(7)～式(9)可以發現，方程式中K即為機車垂向振動方程的剛度矩陣[20]，矩陣中的每一項kij表示由于第j個單位位移而引起的第i個作用力；A為考慮車鉤和牽引點高度變化時的系數矩陣，如果不考慮牽引點高度變化的影響可令Aij=0；X為車體和前后轉向架位移向量；F為外力向量，提供車鉤力和牽引電機作用力的作用信息，向量中各項可由受力分析方便得到。正因如此，可直接通過機車垂向振動模型受力分析來構建系統剛度矩陣和外力向量，這種方法比前述的幾何關系推導法簡單明了，且不易出錯，其通用性主要體現在以下幾個方面：

1)適用于C0-C0 軸式、2(B0-B0)軸式等多種結構形式機車。雖然以上軸重轉移求解矩陣是針對六軸機車推導建立的方程，對于單節四軸機車同樣適用，只需要在轉向架兩軸中間加一條虛擬軸，在二系懸掛中間加一對虛擬彈簧(橡膠堆)，并將虛擬軸和虛擬彈簧(橡膠堆)的剛度設為0。

2)適用于不同牽引桿類型的情況。能夠方便處理牽引桿為斜拉桿的機車，當二軸轉向架機車采用斜牽引桿時，只需在式(7)的右側附加另一外力向量：

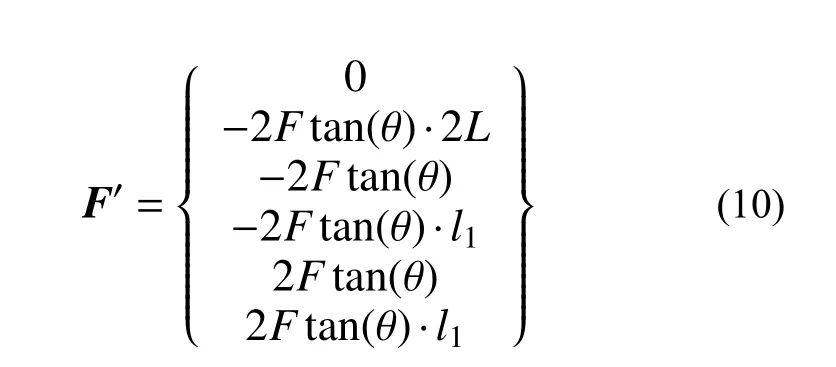
其中， θ為牽引拉桿與水平面的夾角。這里規定，當牽引桿位于車體中部時 θ為正值，位于車體兩端時 θ為負值。

3)上述方程推導針對牽引電機軸懸式機車，對于牽引電機架懸式機車，只需要修改方程式(7)中的電機相關系數即可。

通過求解方程式(7)可以得到機車牽引列車時的各部分垂向位移和點頭角位移，進而方便地得到各軸軸重變化量：

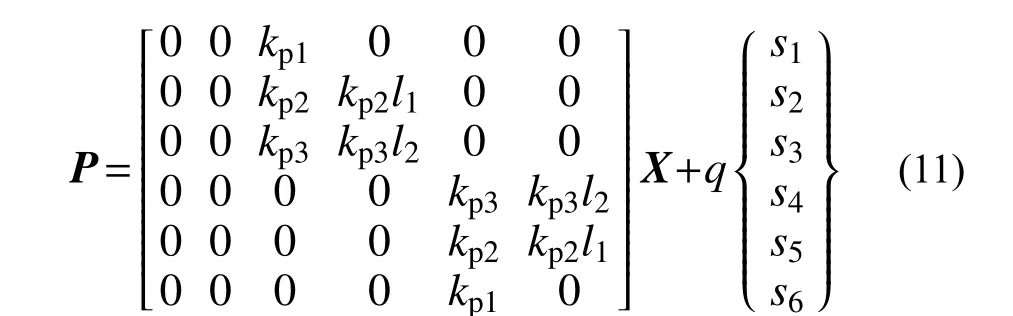
由式(11)計算得到各軸軸重轉移量后便可求解各軸的黏著系數利用率，進而可以方便快捷地分析機車的理想牽引高度等。

2 后端連掛車鉤垂向約束影響分析

本文計算模型中采用具有一定剛度的線性彈簧約束來等效模擬后端連掛車鉤的垂向約束作用，通過改變等效約束剛度的大小來體現車鉤鉤頭垂向約束作用的大小。假設該等效約束剛度從0 kN/m 到1×1015kN/m 逐漸增大，分別計算不同等效約束剛度下的機車軸重轉移情況。

采用某HX 系列重載電力機車計算參數，軸式為2(B0-B0)，牽引電機裝置采用軸懸式對稱布置。表2 列出了不同等效約束剛度下的機車軸重變化和前鉤鉤頭垂向位移。圖4～圖6 分別給出機車運動形態、機車各軸黏著利用率以及前端車鉤抬升量隨等效約束剛度的變化曲線圖。

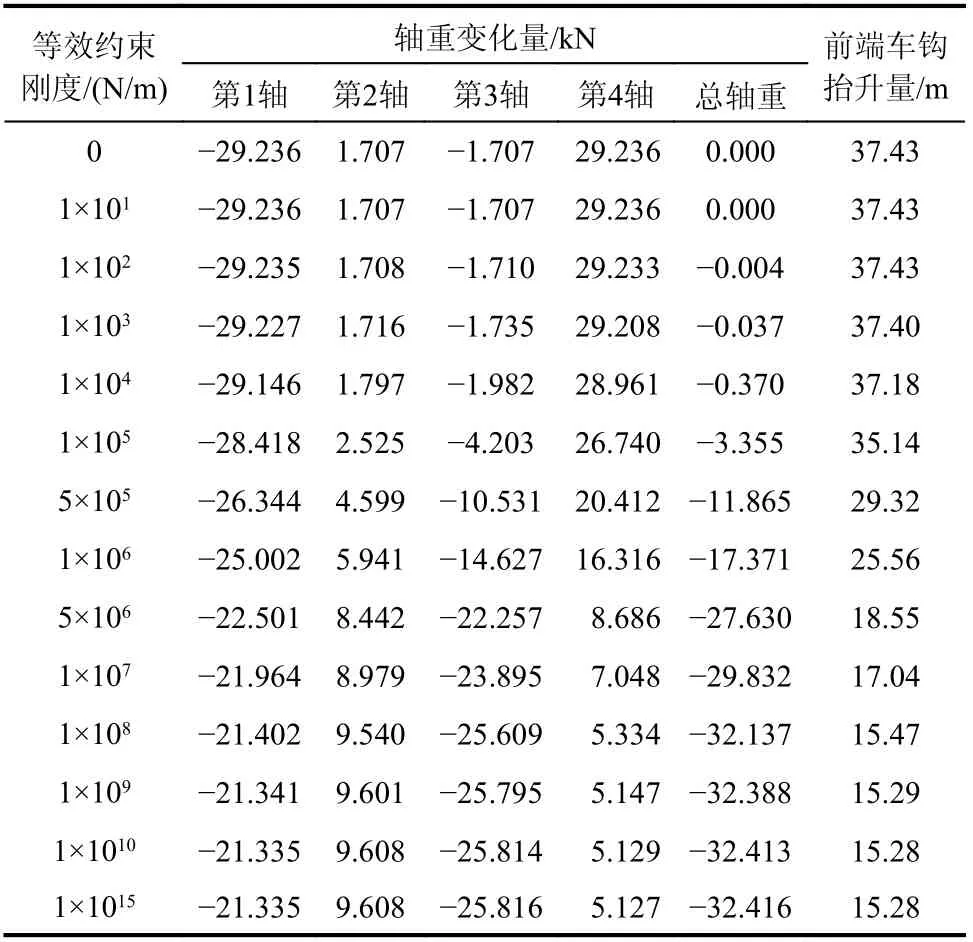
表2 不同車鉤等效約束剛度下機車軸重轉移情況Table 2 Locomotive axle load transfer under different coupler equivalent restraint stiffness

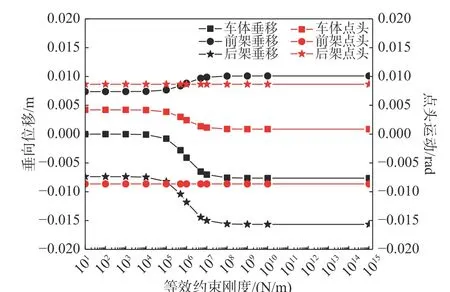
圖4 各部分運動變化量隨等效約束剛度變化曲線圖Fig. 4 Variation of locomotive carbody motions with coupler equivalent restraint stiffness

表2 中后端車鉤等效約束剛度為0 即為不考慮后端車鉤垂向摩擦約束作用的情況。由表2、圖4 可見，隨著等效約束剛度的增大，機車車體和轉向架運動形態會發生變化，車體垂向位移和點頭角位移逐漸減小，前、后轉向架垂向位移在原有基礎上逐漸增大，而它們的點頭角位移基本保持不變，這說明隨著后端車鉤鉤頭約束作用的增大，前、后轉向架運動的增大一定程度上彌補了車體運動的減小。

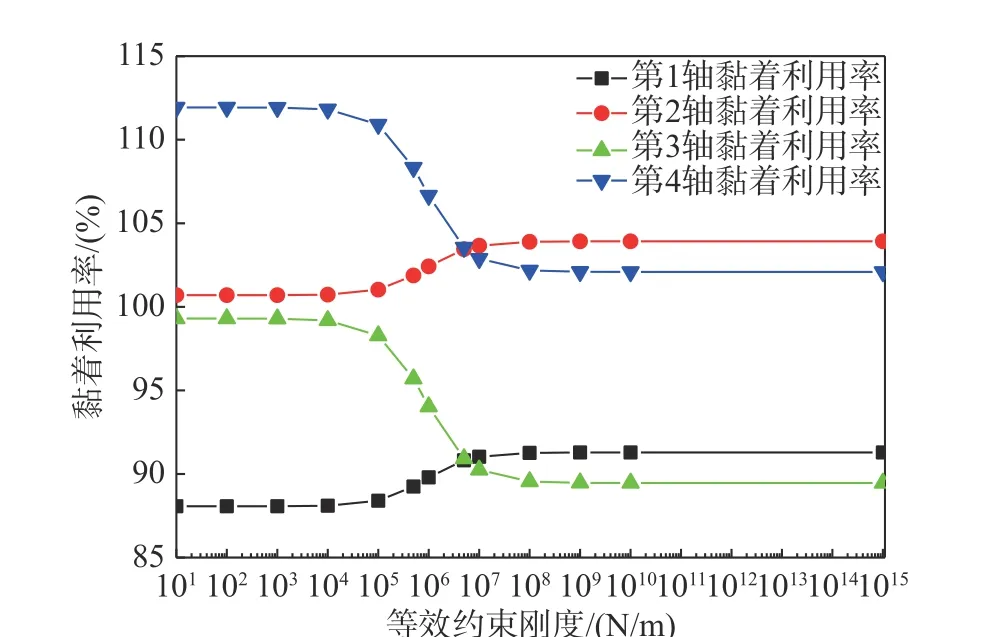
圖5 機車各軸黏著利用率隨等效約束剛度變化曲線圖Fig. 5 Variation of locomotive adhesion utilization ratios with coupler equivalent restraint stiffness

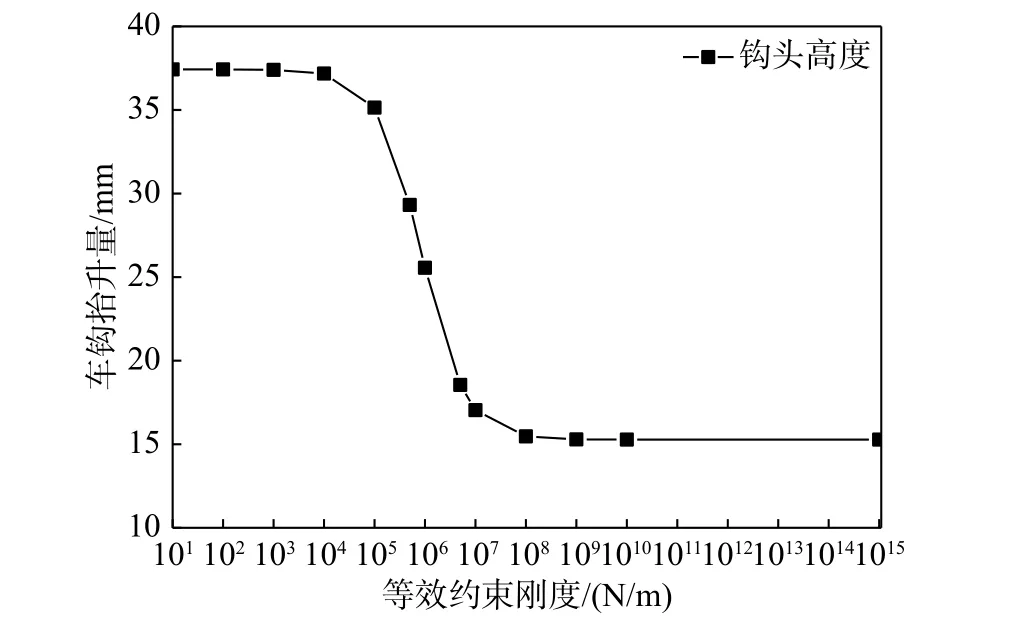
圖6 機車車鉤抬升量隨等效約束剛度變化曲線圖Fig. 6 Variation of coupler lifting with coupler equivalent restraint stiffness

當不考慮后端車鉤垂向約束(等效約束剛度為0)時，第1 軸、3 軸軸重處于減載狀態，第1 軸減載量達到29.236 kN；隨著等效約束剛度的增大，機車各軸軸重有明顯變化，第1 軸、3 軸雖然仍處于減載狀態，但是隨著后端車鉤垂向約束的增大，第1 軸減載逐漸減弱，而第3 軸減載量逐漸增大并超過第1 軸。相應地，機車各軸黏著利用率具有與軸重相同的變化規律，而根據機車黏著利用率等于各軸最小黏著利用率的原則，從圖4可以看出，在等效約束剛度小于5×106N/m 時，機車黏著利用率取第1 軸黏著利用率，且逐漸減小；而在等效約束剛度大于5×106N/m 后，便取第3 軸黏著利用率，且逐漸增大。另外，機車各軸總軸重隨著后端車鉤垂向約束的增大會出現逐漸增大的減載量，當等效約束剛度1×1015N/m 時，即后端車鉤完全約束狀態時，整個機車約減載3.2%。

最后分析前端車鉤抬升量隨后端車鉤垂向約束作用的變化規律。用于計算分析的重載機車專門進行了機車滿功率牽引起動時的車鉤抬升量測定試驗，具體方法為：重載列車停放于平直道，后部貨車大列施加空氣制動，前部機車施加牽引力，在前端鉤頭下部設置一塊調整為水平狀態的平板，在鉤頭位置布置垂向激光測距儀對準平板測量車鉤抬升量。當機車施加滿級牽引力760 kN時，前端車鉤抬升量測定值為20 mm，介于等效約束剛度為0 N/m 和1×1015N/m 之間，說明機車實際牽引時，后端車鉤確實在拉鉤力作用下對車體產生了垂向約束作用，但是該垂向約束并未達到完全剛性約束狀態，充分印證了本文的分析結論。從表2 中可知，當等效約束剛度取5×106N/m時，車鉤抬升量18.55 mm，接近實際測定值，因此在實際軸重轉移計算時，可以將等效約束剛度取值控制在5×106N/m 左右。此時根據表2 計算可得，該機車黏著利用率由不考慮車鉤垂向約束作用的88%提高至等效約束剛度取值5×106N/m 時的91%，提高了3%。

3 六軸機車軸重轉移影響因素分析

本節采用所建立的通用計算方法對某C0-C0軸式電力機車的軸重轉移情況進行計算，分析機車一系和二系懸掛垂向剛度、牽引點高度等因素對其軸重轉移的影響。機車軸重25 t，每軸起動牽引力為95 kN，車鉤距離軌面高度0.88 m，轉向架第1 軸、3 軸距離第2 軸的縱向距離分別為2.25 m、2.00 m，定距為12.32 m，牽引方式采用水平牽引桿，電機吊掛方式為軸懸式，電機吊桿到車軸的縱向距離為1.171 m，每軸一系懸掛垂向合成剛度為3400 kN/m，二系懸掛采用橡膠堆，每個縱斷面橡膠堆垂向合成剛度為12 000 kN/m，二系橡膠堆到轉向架第1 軸的縱向距離分別為1.1825 m、1.5175 m、3.35 m。

首先分析機車一系垂向剛度對軸重轉移的影響，假設一系垂向剛度在2200 kN/m～4600 kN/m每隔400 kN/m 取值，圖7 給出了機車各軸軸重變化量隨一系垂向剛度的變化曲線圖，圖8 給出了相應的黏著系數利用率隨一系垂向剛度的變化規律圖。可以看出，隨著一系垂向剛度的增大，機車第1 軸減載量逐漸增大，第2 軸減載量逐漸減小，第3 軸由減載逐漸變為增載，機車黏著系數利用率逐漸減小。

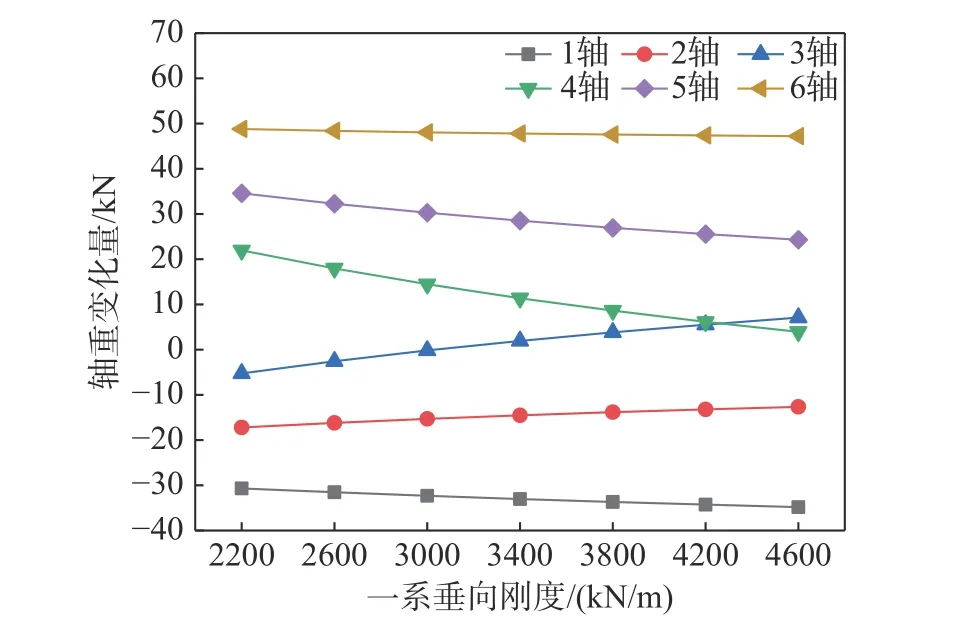
圖7 各軸軸重變化量隨一系垂向剛度變化曲線圖Fig. 7 Variation of locomotive axle load transfer with primary suspension vertical stiffness

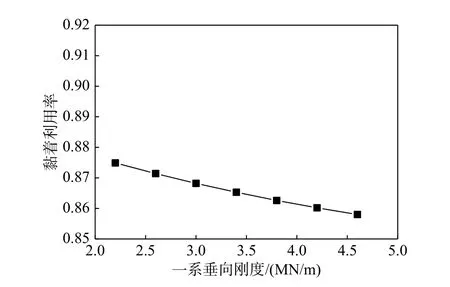
圖8 機車黏著系數利用率隨一系垂向剛度變化規律圖Fig. 8 Variation of locomotive adhesion utilization ratios with primary suspension vertical stiffness

假設二系垂向剛度在9000 kN/m～15 000 kN/m范圍內每隔1000 kN/m 取值，分析二系垂向剛度變化對機車軸重轉移的影響。圖9 給出了機車各軸軸重變化量隨二系垂向剛度的變化曲線圖，圖10給出了相應的黏著系數利用率隨二系垂向剛度的變化規律圖。可以看出，隨著二系垂向剛度的增大，機車第1 軸減載量逐漸減小，第2 軸減載量逐漸增大，第3 軸增載量逐漸減小，后轉向架三個軸與前轉向架正好相反，且機車黏著系數利用率逐漸增大。二系垂向剛度增大會使得二系垂向位移減小，轉向架轉角相應減小，從而減弱機車軸重轉移。假設機車牽引點高度從-75 mm～725 mm 按照間隔100 mm 遞增，分析牽引點高度變化對機車軸重轉移的影響。圖11 給出了機車各軸軸重變化量隨牽引點高度的變化曲線圖，圖12 給出了相應的黏著系數利用率變化規律圖。可以看出，當牽引點高度為負值或者很小時，第3 軸軸重減載大于第1 軸，且減載量隨牽引點高度增大逐漸減小；隨后當前牽引點高度逐漸增大時，第1 軸軸重減載逐漸增大，第2 軸軸重減載量逐漸減小，機車黏著系數利用率隨之明顯減小。可見牽引點高度對軸重轉移具有明顯影響，其影響程度要大于一系和二系懸掛垂向剛度。

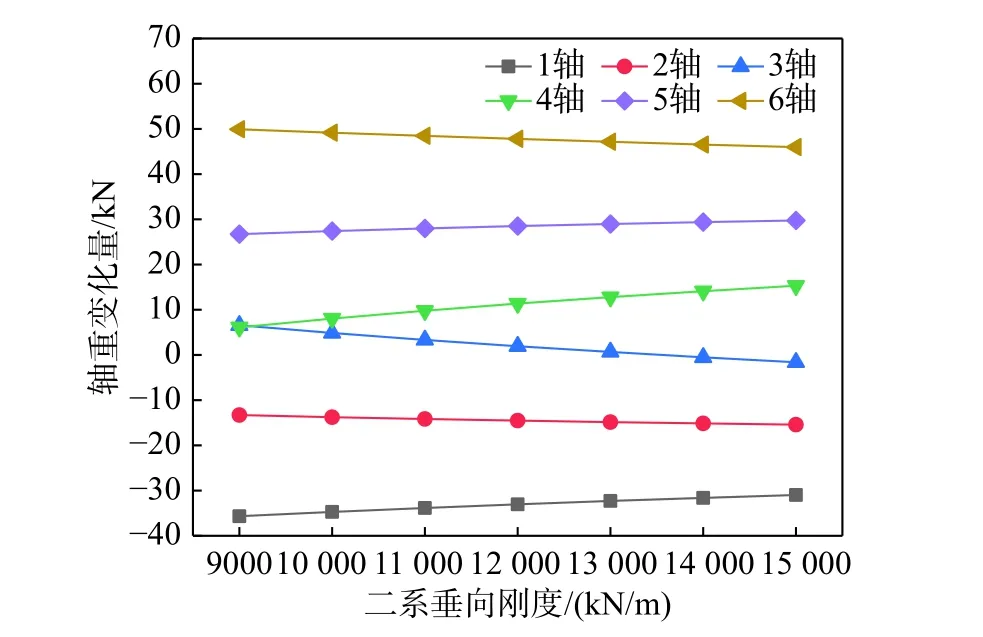
圖9 各軸軸重變化量隨二系垂向剛度變化曲線圖Fig. 9 Variation of locomotive axle load transfer with secondary suspension vertical stiffness

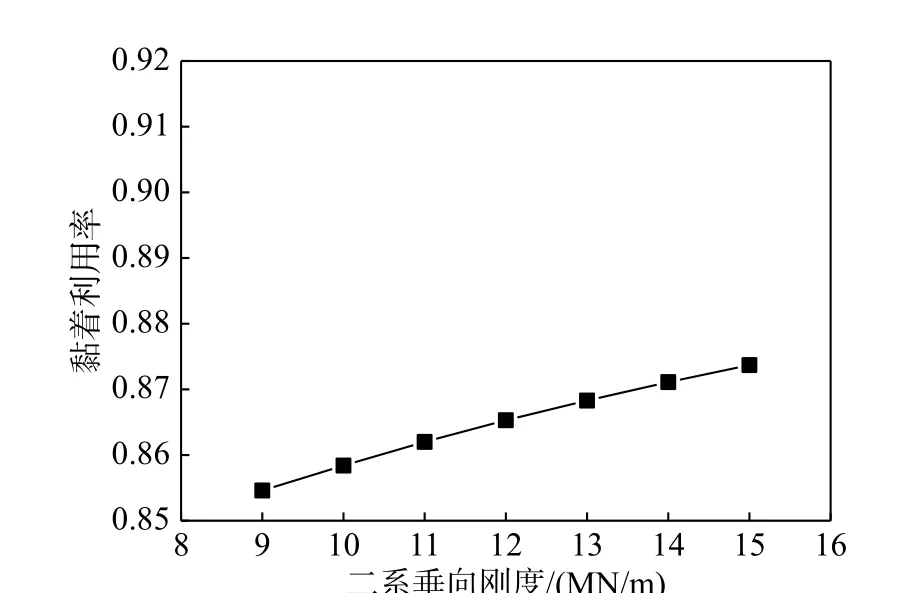
圖10 機車黏著系數利用率隨二系垂向剛度變化規律圖Fig. 10 Variation of locomotive adhesion utilization ratios with secondary suspension vertical stiffness

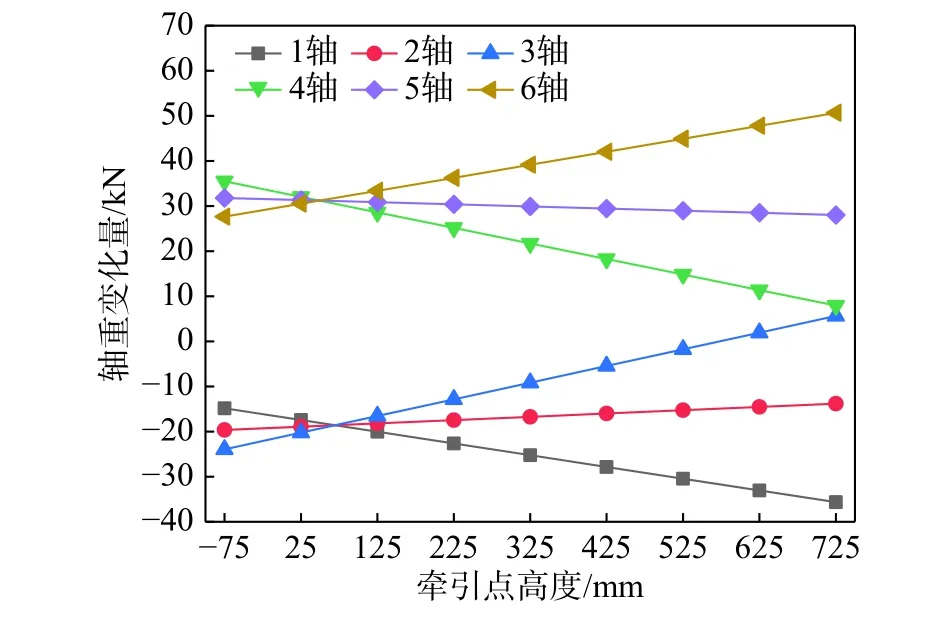
圖11 各軸軸重變化量隨牽引點高度變化曲線圖Fig. 11 Variation of locomotive axle load transfer with traction point height

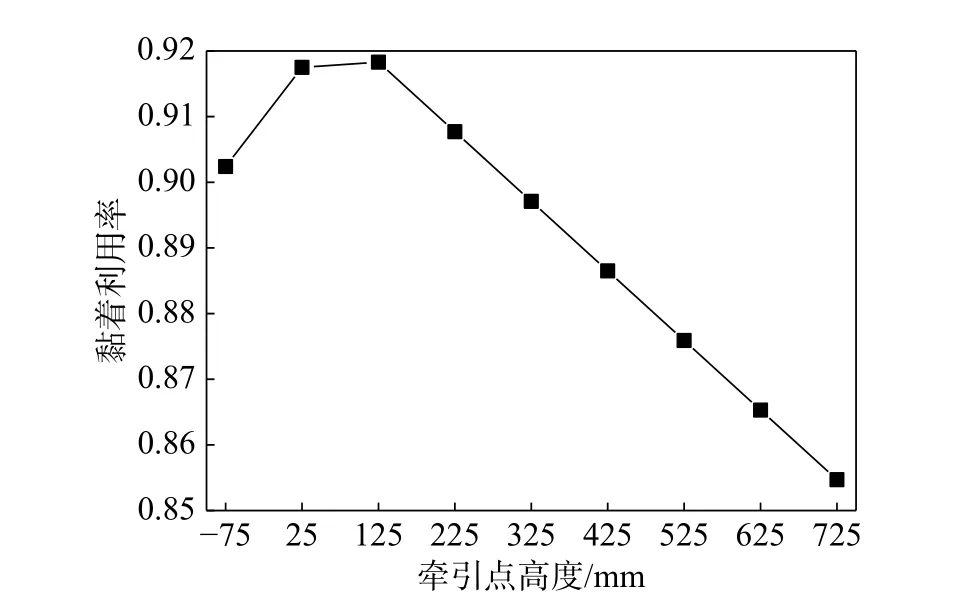
圖12 機車黏著系數利用率隨牽引點高度變化規律圖Fig. 12 Variation of locomotive adhesion utilization ratios with traction point height

4 結論及展望

針對機車軸重轉移計算相關問題，本文建立了考慮車鉤垂向約束作用的機車軸重轉移通用計算方法，結合試驗數據確定了車鉤等效約束剛度的取值范圍，并采用所編制的計算程序分析了后端車鉤垂向約束、結構懸掛參數等對機車軸重轉移的影響規律。研究結論主要包括以下幾點：

(1)機車牽引時后端連掛車鉤鉤頭接觸面在拉鉤力作用下產生的垂向約束作用會對機車軸重轉移產生明顯影響，結合某HX 系列2(B0-B0)軸式機車車鉤抬升量試驗結果確定該車等效約束剛度合理的取值約為二系橡膠堆到轉向架第1 軸的縱向距離為5×106N/m，其黏著利用率較不考慮車鉤垂向約束時提高了3%。

(2)所建立的基于剛度矩陣的機車軸重轉移計算方法能夠綜合考慮牽引點高度變化、機車斜拉桿的影響作用，簡便、準確地對各種類型機車進行軸重轉移計算，具有較好的通用性。

(3)機車懸掛參數和牽引點高度均對其軸重轉移具有影響作用，并且牽引點高度影響最為顯著，牽引點高度增大會加劇軸重轉移。

目前機車軸重轉移主要通過計算分析得到，軸重轉移相關試驗研究很少見到。正因如此，機車軸重轉移的計算分析結果并未通過試驗數據進行驗證和修正，本文并未得到各軸軸重變化量測試數據，僅通過機車牽引工況的前端車鉤抬升量測定試驗對計算結果進行了側面校驗。為了校驗和改進機車軸重轉移計算方法，有必要開展機車軸重轉移試驗測試相關研究工作。