基于BFO-LSSVM模型的爆破料級配預測研究

余良松 趙倫 彭勇 惠紅強

摘要：為實現爆破級配曲線的準確預測，借助細菌覓食算法（BFO）及最小二乘支持向量機（LS-SVM）理論構建基于BFO算法的LS-SVM優化模型（BFO-LSSVM）。使用35組爆破數據作為訓練樣本對模型預測精度進行檢驗，選取孔排距、堵塞、孔深等因素作為輸入因子，爆破料級配作為預測模型輸出因子。結果表明，BFO-LSSVM預測模型的預測結果精度高于相同樣本容量下LS-SVM模型。以阿爾塔什水利樞紐工程料場開挖爆破數據為例，BFO-LSSVM模型預測結果平均誤差為1.47%，驗證了該預測模型的可行性及實用性。

關鍵詞：爆破級配;塊度預測;最小二乘支持向量機;細菌覓食算法

隨著我國經濟的不斷發展，基礎建設也隨之不斷擴大，越來越多的不同尺寸的石料被廣泛的運用于水利工程（堆石壩、防洪堤）、建筑等工程。鉆孔爆破是石料開采的主要手段之一，其中爆破塊度及其大小分布是評價石料開采爆破優劣的主要參數之一，爆破塊度過大會導致二次破碎成本增加以及增大運輸難度。另一方面，在堆石壩填筑時，爆破塊度的級配也會對壩體的密實度產生直接影響。

目前，國內外科研工作者針對爆破塊度分布進行了大量研究，提出了眾多計算理論及預測模型。如武仁杰和李海波等基于多元回歸分析方法建立了塊度預測模型，并通過對比實測爆破跨度統計數據，驗證了該預測模型的正確性;李瑞澤等利用三維激光掃描技術對爆破碎石顆粒形狀及表面積開展了詳細研究。Cunninghan綜合考慮爆破參數、巖體性質及炸藥單耗等因數條件下，利用Kuznetsov方程與R-R方程相結合的方法對X50展開了研究。吳新霞等結合實際工程背景，在Kuz-Ram模型基礎上研究并提出了適用于天生橋以及水電站筑壩級配料預測模型。

傳統預測方法由于輸入參數較少，且依賴于特定條件下爆破實測數據，因此建立的爆破塊度預測模型通用性較差。隨著計算機科學的發展，利用計算機處理能力分析預測爆破塊度也得到了廣泛運用，如遺傳算法、支持向量機法、神經網絡法等。王澤文等綜合考慮裝藥工藝、巖體性質及爆破參數等影響因素，建立了基于PSO-ELM的爆破塊度預測模型。史秀志等基于最小二乘支持向量機思想，構建了適用于小樣本條件下的預測模型。

綜上所述，綜合考慮巖體性質、炸藥類型、爆破參數等因素，實現巖體爆破后塊度的預測已成為巖體爆炸力學領域熱點問題之一，并取得了一定得進展。但現有基于經驗公式法建立的預測模型考慮因素較少，且人工神經網絡法預測結果受隱含層節點數影響較大，學習效果較差。

基于此，本文依托實測爆破數據，將細菌覓食算法（BFO）引入到最小二乘支持向量機（LSSVM）中，利用細菌覓食算法全局搜索能力強等特點優化最小二乘支持向量機參數，構造BFO-LSSVM爆破塊度預測模型，進而實現爆后級配曲線的準確預測。

1 最小二乘支持向量機算法

1.1 支持向量機

支持向量機（Support Vector Machine）是由Vapnik等提出來的一種二級分類模型。SVM具有模型精度較高，適應能力優良，并且有著優秀的魯棒性以及泛化能力等特點。在爆破塊度的結果預測中，因為影響塊度分布的因素眾多，利用SVM方法通過選擇映射函數（核函數）將塊度分布的結果與巖體性質、炸藥類型、爆破參數等多影響因素之間的非線性關系映射成為高維空間的線性關系，進而實現爆破塊度的準確預測。

1.2 最小二乘支持向量機

最小二乘支持向量機（Least Squares Support Vector Machine）是一種針對SVM的改進算法，通過將比較目標函數誤差的平方項結果作為算法的優化評判標準，并將計算過程中的約束條件變為等式約束達到降低求解難度、提高求解效率等目的。基本原理如下：

對于樣本，采用與支持向量機相同的算法理論，構造出最小二乘支持向量機的目標函數為：

2 BFO-LSSVM爆破塊度預測模型的建立

2.1細菌覓食優化算法（Bacteria Foraging Optimization）

細菌覓食優化算法是2002年由Passion基于大腸桿菌的覓食行為提出的一種智能優化算法，大量數據分析表明，該算法具有全局搜索能力強、魯棒性強等優點。該算法根據覓食的四個基本行為（趨向性、聚集性、復制性和遷徙性）求解工程問題。

（1）趨向性：大腸桿菌的覓食過程中有兩個動作：旋轉和游動。旋轉是為了找到一個新的方向運動，而游動則是繼續按照之前的方向運動。趨向性操作的本質就是對這兩個動作的模擬。

式中：表示細菌i在第j次趨化第k次復制第l次驅散后的位置。

（2）聚集：細菌覓食過程中，不同個體存在斥力與引力兩種作用力，其中斥力使細菌在一定區域內單獨覓食，引力則使細菌向特定區域聚集。其聚集的數學表達式為：

（3）復制：細菌進化過程服從優勝劣汰原則，其中覓食能力強的細菌進行復制。表達式為：

（4）遷徙：當細菌所處壞境發生突變時，算法給定一定概率模擬細菌遷徙過程，使細菌個體在概率死亡條件下產生一個新個體，該行為有利于算法跳出局部最優解。

2.2 基于BFO優化的LSSVM模型

采取基于BFO算法優化LS-SVM參數，運用經過優化后的LS-SVM來對爆破塊度的分布進行預測。首先讀取爆破塊度的數據，把數據分為訓練樣本和預測樣本，然后利用BFO算法計算出LS-SVM的最優參數，再將獲得的最優參數的值代入LS-SVM中對訓練樣本進行訓練，最后對預測樣本進行分析，計算出相對應的結果。

算法的流程圖如下所示：

2.3 不同預測模型對比分析

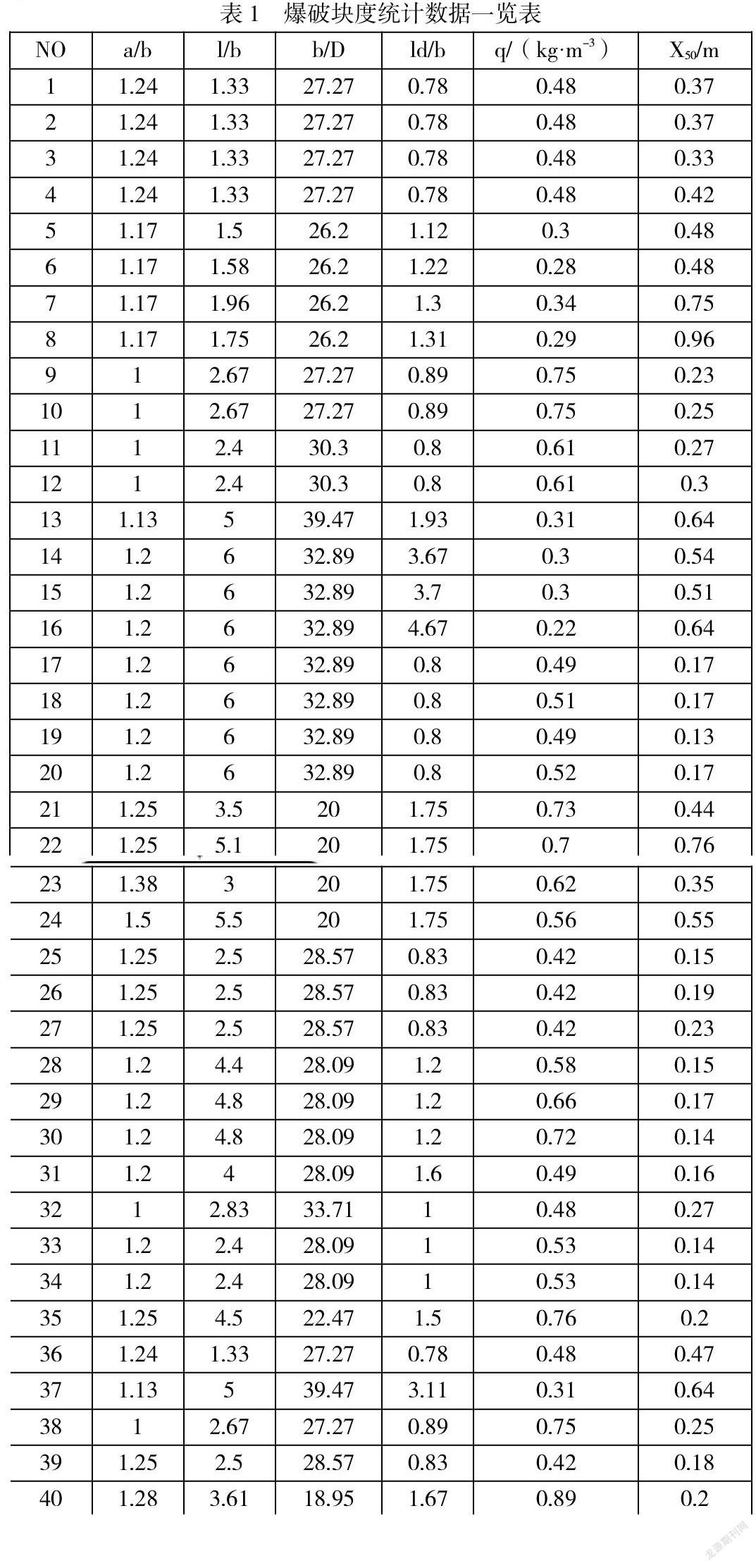
取40組文獻中的露天礦山爆破塊度統計數據，其中前35組數據為訓練樣本，后5組為模型預測精度驗證測試樣本，取相對誤差及平均絕對誤差作為計算指標，用來評估LS-SVM、BFO-LSSVM預測模型的預測精度。爆破塊度統計數據見表1。各模型預測結果見表2及圖1。

從表2可以看出，兩種不同預測方法的平均絕對相對誤差分別為16.72%和5.22%。由圖2可知，BFO-LSSVM模型的擬合度較高，除了第一組的預測值相對誤差稍大，另外四組預測結果相當好;反觀LS-SVM模型，預測的穩定性不高，存在個別預測樣本值誤差過大的問題。綜上可知，由BFO優化后的LSSVM模型比原模型有更高的預測精度，且數據擬合能力更強。

3 工程案例分析

3.1 工程概況

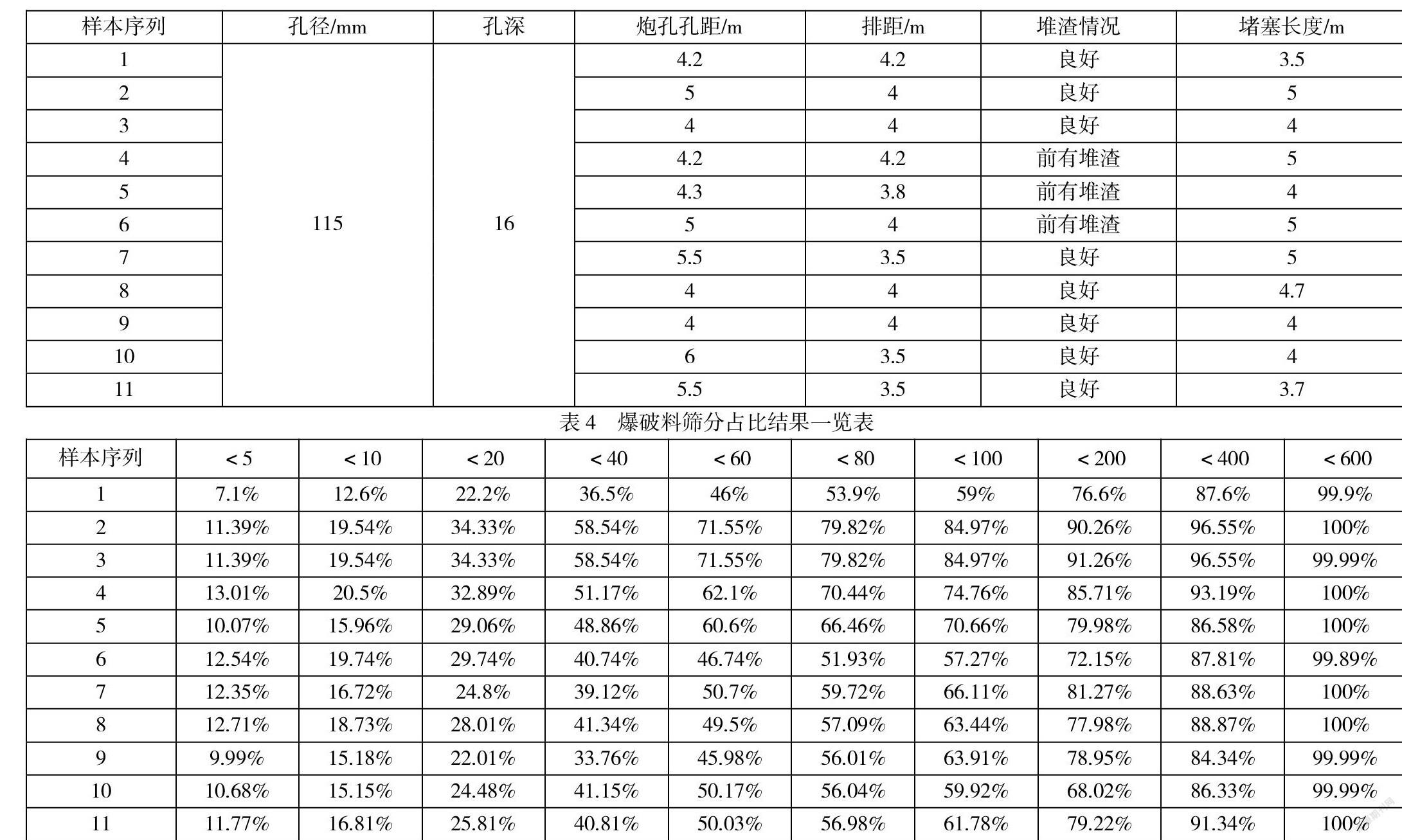
阿爾塔什水利樞紐工程位于喀什地區莎車縣和克孜勒蘇克爾克孜自治州阿克陶縣交界處，是葉爾羌河干流山區下游河段的控制性水利樞紐工程，是葉爾羌河干流梯級規劃中“兩庫十四級”的第十一個梯級，規劃水庫正常蓄水位1820米，最大壩高164.8米，水庫總庫容22.49億立方米。為滿足工程大壩澆筑過程中用料需求，現場需進行爆破試驗。通過爆破試驗對參數進行調整，以保證料場開挖所提供的石料級配滿足設計要求。根據現場交通及巖體出露狀態，選取P1料場開挖區11組實測爆破料篩分數據，爆破參數如表3所示，各次爆破料篩分結果見表4。選組前10組作為訓練樣本，剩余1組作為預測樣本。

3.2 預測結果分析

通過爆破試驗，獲取石料開挖爆破料粒徑篩分結果，結合現場各次爆破試驗相應爆破設計參數，通過建立的BFO-LSSVM預測模型，進行爆破料塊度級配預測，并與實測值分析比較。

（1）根據前10組訓練樣本爆破料篩分結果，結合對應爆破試驗參數，用BFO-LSSVM進行訓練，確定BFO算法的參數值，如表所示。通過對訓練樣本數據的爆破料粒徑與爆破參數分析可知，爆破料粒徑大小與爆破孔網參數成正相關，即爆破料大小隨孔網參數增加而增大。

（2）根據所建立的BFO-LSSVM預測模型，基于前10組訓練樣本進行訓練的基礎上，對第11次爆破料級配進行預測，預測結果如表5所示。

從表5中可以看出，爆破料級配的預測結果依次為10.9、16.89、28.13、42.54、52.8、54.82、59.86、78.88、88.82、99.97。將預測結果與實際結果進行對比分析可以看出，BFO-LSSVM模型預測結果最大誤差僅為2.52%，平均誤差為1.47%，預測結果誤差控制的相當小，能滿足工程實際的需求。

結語

（1）基于最小二乘支持向量機構理論，構造了基于BFO-LSSVM的爆破塊度預測模型。通過LS-SVM模型和BFO-LSSVM模型的預測結果對比，結果表明，BFO算法可在一定程度上對LS-SVM模型的性能進行優化，使誤差從16.72%降低到5.22%，即BFO-LSSVM模型在爆破料級配的預測中具有比LS-SVM模型更高的預測精度。

（2）基于BFO-LSSVM塊度預測模型對阿爾塔什水利樞紐工程堆石料開采過成中收集的爆破料級配數據進行了級配曲線的預測，其預測平均誤差為1.47%，進一步證明了在確定的爆破參數和現場巖體條件下，爆破料級配預測的可行性，對壩料的控制開采具有重大的意義。

（3）基于小樣本對爆破料級配預測時，訓練樣本數據的準確性對模型預測結果的精度有較大的影響。同時BFO-LSSVM模型應用過程中沒有考慮結構面對爆破塊度的影響，使得文中模型的預測結果只適用于巖性相同或相近的料場。

參考文獻（References）

[1]梁向前，傅海峰. 面板堆石壩壩料爆破開采技術研究進展[J]. 水利規劃與設計，2007，5：71-73.

[2]Norazirah A，Fuad S，Hazizan M. The Effect of Size and Shape on Breakage Characteristic of Mineral[J]. Procedia Chemistry，2016，19：702-708.

[3]朱晟，寧志遠，鐘春欣，等. 考慮級配效應的堆石料顆粒破碎與變形特性研究[J]. 水利學報，2018，49（7）：849– 857.

[4]武仁杰，李海波，于崇，等. 基于統計分級判別的爆破塊度預測模型[J]. 巖石力學與工程學報，2018，37（1）：141-147.

[5]李瑞澤，盧文波，尹岳降，等. 白鶴灘旱谷地灰巖爆破碎石顆粒形狀及比表面積特征研究[J]. 巖石力學與工程學報，2019，38（X）：1-11.

[6]Cunningham C. 預估爆破破碎的KUZ-RAM模型[J]. 第一屆爆破破巖國際會議論文集，長沙巖石力學工程技術咨詢公司編譯，1985：251-257.

[7]吳新霞，彭朝輝，張正宇，等. Kuz-Ram模型在堆石壩級配料開采爆破中的應用[J]. 長江科學院院報，1998，4：40-42+46.

[8]祝文化，朱瑞賡，夏元友. 爆破塊度預測的神經網絡方法研究[J]. 武漢理工大學學報，2001，1：60-62.

[9]郝全明，楊振增. BP神經網絡在巖層爆破參數優化中的應用[J]. 煤炭技術，2014，33（12）：20-22.

[10]王澤文，左宇軍，趙明生，等. 基于PSO-ELM的爆破塊度預測研究[J]. 礦業研究與開發，2019，39（06）：136-139.

[11]史秀志，王洋，黃丹，等. 基于LS-SVR巖石爆破塊度預測[J]. 爆破，2016，33（3）：36-40.

作者簡介：余良松（1976年7月—），男，漢，浙江杭州人，碩士，高級工程師，研究方向：水利水電工程施工。