蟻群算法在0-1背包問題中的研究與實現

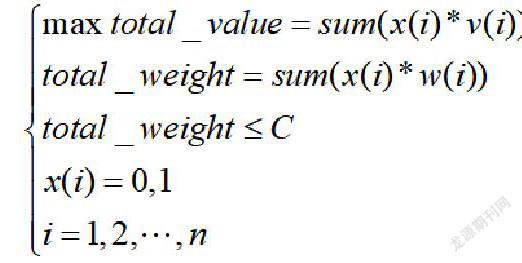
摘要：蟻群算法也稱為螞蟻算法，即模擬螞蟻從居住地出發去尋找食物源的過程，它在一定程度上可以看成是一種用來在圖中尋找最優路徑的算法。該算法已成功地應用于許多離散問題。隨著研究的深入與應用領域的逐步擴展，蟻群算法已經在智能領域顯示出了較為重要的地位，對于解決各種復雜優化問題都顯示出了它的優點。0-1背包問題是一個經典算法，在實際生活中應用較為廣泛，例如在材料切割、貨物裝箱、車間調度等問題中都有相關的應用。本文主要實現了蟻群算法解決0-1背包問題，首先研究了蟻群算法的基本原理及算法思想，然后在MATLAB下實現了蟻群算法求解0-1背包問題。實驗表明，算法運行結果正確，穩定性好。

關鍵詞：蟻群算法;0-1背包;信息素;揮發因子

中圖分類號：TP 391

引言

蟻群算法是一種群體智能理論的優化算法，蟻群算法的基本思想是根據螞蟻從蟻巢出發去尋找食物源的過程得出的。蟻群算法如今也多用于求解旅行商問題，隨著網絡科技的發展，網購等在人們的生活中所占比重越來越大，還有近幾年流行的‘UU跑腿’等，這些實際生活中的問題都會用到蟻群算法，該算法已經成功地應用到了許多離散問題中，在國際群體智能計算領域，蟻群算法已經成為一個熱門的研究方向。

背包問題最早是由 Dantzing在 20 世紀50 年代首次提出的，應用已經越來越廣泛。背包問題是指：對于n個物品和一個背包，當知道每個物品的重量和價值以及背包所能承受的最大重量時，從這些物品中選出若干件放入背包中，使得背包的重量小于背包所能承受的最大重量，并且背包的總價值能夠達到最大。背包的總價值等于裝入背包的物品價值之和，找出一種放入物品的方案能同時滿足上述兩個條件。

記背包的總重量為為total_weight，總價值為total_value，x（i）=1表示將第i個物品放入背包，x（i）=0表示未放入，根據0-1背包問題的算法原理，可將其數學模型表示為如下：

1? 蟻群算法的算法思想

蟻群算法是指螞蟻從蟻巢出發去尋找食物的過程中，當蟻巢到食物源的距離越短，則螞蟻從巢到食物源，然后再返回巢的時間越短。這相當于在相同的時間內，路徑越短螞蟻會分泌和積累越多的信息素，而隨后去尋找食物的螞蟻會根據前面螞蟻分泌的信息素來判斷哪條路徑最短，以便能夠快速準確的選擇哪條路徑。所以某條路徑上的信息素越多，螞蟻選擇這條路的可能性就越大。

2? 蟻群算法實現0-1背包的算法步驟

蟻群算法的算法步驟如下：

（1）初始化參數：設置蟻群參數，背包相關的參數，路徑信息素等參數;

（2）螞蟻移動：后續出發的螞蟻根據前面螞蟻留下的信息素含量和一定的概率來選擇要行走的路徑，在實現0-1背包問題中計算某個物品被選擇的概率;

（3）螞蟻要行走的路線信息更新：根據（2）中計算的概率，螞蟻將選擇某條路徑，同時將對應的物品添加到路徑中;

（4）判斷是否滿足條件：判斷將物品添加到背包后是否滿足條件，并更新背包的價值的重量;

（5）評價蟻群：計算一次循環結束后的最優值，將其與全局最優值比較，判斷是否需要更新全局最優值。

3? 算法實現

（1）初始化參數：定義物品的價值，重量以及背包能承受的最大重量;定義信息素揮發因子為r，全局最優解為Jie_best，全局最優值為value_best，定義最大迭代次數為count ;

（2）從i=1到count循環遍歷：定義一個零矩陣用以存儲m只螞蟻的路徑，j從1到n開始循環，根據信息素的重要因子（a）及吸引因子（b）計算每個物品被選擇的概率。

for j=1：n

d=d+t（j）^a*（value（j）/weight（j））^b;

end

for j=1：n

q（j）=t（j）^a*（value（j）/weight（j））^b/d;

end

（3）選擇物品放入背包：先隨機選取一個物品放入背包，并將其添加到當前對應螞蟻的路徑中，修改背包當前的容量。

x=floor（rand*9）+1;

D（k，x）=1;

W_now=weight（x）;

（4）更新路徑及背包信息：利用輪盤賭法，信息素揮發系數計算下一個物品被選擇的概率，如果滿足背包容量限制條件則將其加入背包中，并更新當前螞蟻的路徑信息和背包信息。

j=roulette_wheel（u，temp）;

u=u-temp（j）;

Temp（j）=0;

if（W_now+weight（j）<=W）

D（k，j）=1;

W_now=W_now+weight（j）;

（5）更新全局最優值：一次迭代完成后將本次迭代的最優值與全局最優值對比，根據對比結果重新定義全局最優值。

[p_best（i），J]=max（D*value’）;

if（value_best<p_best（i））

value_best=p_best（i）;

Jie_best=D（J，：）;

4? 運行結果

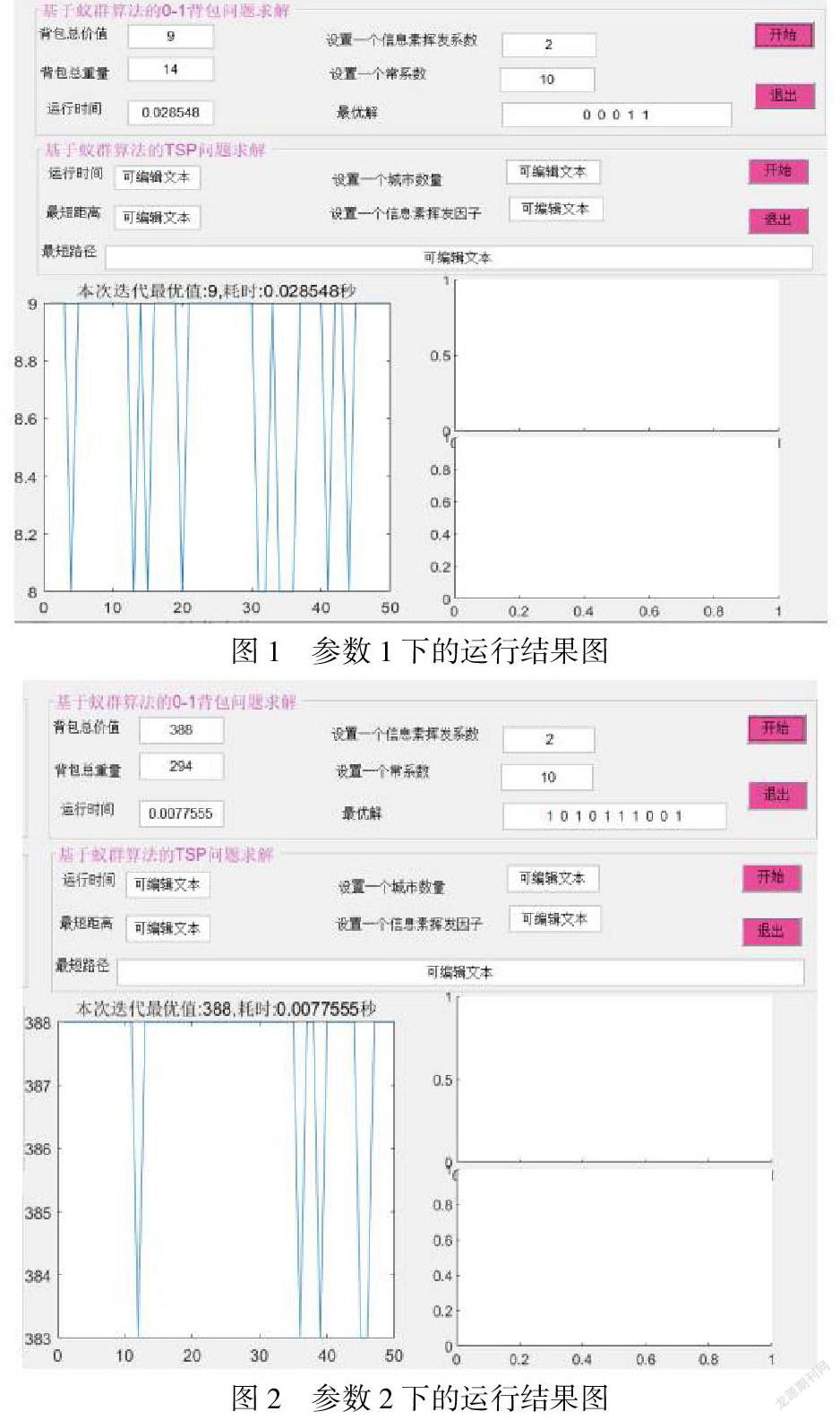
圖1是輸入5個物品時的運行結果，隨機輸入5個物品的價值和重量可由蟻群算法求出背包的最大價值，最大重量以及裝入背包的物品序號。由圖1可知，對于給定的物品價值和物品重量，背包的最大容量以及其他相關參數，圖2算法求得背包的最大價值，最大重量以及裝入背包的物品序號，在改變相關參數時背包的價值和重量，最優解不會改變，但是達到最有解的迭代次數會發生相應的變化。在一定的范圍內，當揮發系數增加時，達到最優解的迭代次數越大。這一結果在理論上也可以解釋，因為當信息素揮發系數越大時，后續螞蟻在尋找食物時選到最短路徑的概率就會越小，因此全局找到最短路徑的時間就越長，這一原理體現在0-1背包問題中就是選擇下一個物品裝入背包時，選到使背包最終價值最大的物品的時間會越長。

5? 結語

蟻群算法的研究現在已經達到了相對成熟的水平，已有不少學者進行了大量的研究，提出了很多研究結論和寶貴經驗，本文基于蟻群算法實現了0-1背包問題。針對蟻群算法，雖然它可以應用到貨物配送等問題中，但是在實際的配送中可能需要考慮更多的因素，例如當有物品需要特殊處理或優先配送時需要對蟻群算法進行一定的改進，體現在蟻群算法中就是優先處理有特殊需求的城市頂點，后面將對這一點進行進一步的研究。

參考文獻：

[1]M. Dorigo，V. Maniezzo，A. Colorni，“Ant system optimization by a colony of cooperating agents，” IEEE Transactions on System，Man，and Cybernetics-Part B，1996，26（1）. 8- 41.

[2]M. Dorigo，L.M. Gambardella. “Ant colony system：a cooperative learning approach to the traveling salesman problem，” IEEE Transactions on Evolutionary Computing，1997，1（1）. 53- 56.

[3]胡小兵. 蟻群優化原理、理論及其應用研究[D]. 重慶大學，2004

[4]鄢莉. 0-1背包問題的算法決策分析[J]. 電腦知識與技術，2020，16（04）：259-260+264.

[5]田峰楠，王于. 求解0-1背包問題算法綜述[J]. 軟件導刊，2009，8（01）：59-61.

[6]宋志飛. 基于蟻群算法的TSP問題研究[D]. 江西理工大學，2013.

[7]弓英瑛. 蟻群算法的改進研究與應用[D]. 安徽理工大學，2014.

作者簡介：宇亞衛（1979-），女，陜西乾縣人，碩士，講師，主要從事圖形圖像處理方面的教學和研究工作。