Rayleigh-Geometric分布及其性質研究

姚惠 代勇 胡云學

DOI：10.16661/j.cnki.1672-3791.2108-5042-1377

摘? 要：隨著極值理論的深入研究，復合極值分布廣泛應用于氣象、交通、水文、金融、保險等領域。該文利用極值理論將Rayleigh分布和Geometric分布進行復合，提出了一種新的復合極值分布：兩參數的Rayleigh-Geometric分布。討論了該分布的分布函數、概率密度函數、參數特定取值時密度函數的圖像特征，討論了分布的分位數、眾數等數字特征，討論了分布的生存函數和危險率函數，最后用極大似然法研究了分布參數的點估計。

關鍵詞：Rayleigh-Geometric分布? ?復合極值分布? ?性質? ?極大似然估計

中圖分類號：O212.3? ? ? ? ? ? ? ? ? ? ? ? 文獻標識碼：A文章編號：1672-3791（2021）08（a）-0011-05

Study on Rayleigh-Geometric Distribution and Its Properties

YAO Hui? DAI Yong? HU Yunxue

（School of Mathematics and Statistics， Qiannan Normal University for Nationalities， Duyun， Guizhou Province， 558000 China）

Abstract： With the in-depth study of extreme value theory， the compound extreme value distribution is widely used in meteorology， transportation， hydrology， finance， insurance and other fields. In this paper， Rayleigh distribution and Geometric distribution are combined by using extreme value theory， and a new composite extreme value distribution is proposed， namely two-parameter Rayleigh-Geometric distribution， which is obtained by compounding a Rayleigh and a geometric distribution based on extreme value theory. This paper discusses the distribution properties， probability density function，the graph features of the density function with specific values of parameters， the digital characteristics of distribution， such as quantile， mode and so on， survival function and risk rate function of distribution. Finally utilizes the maximum likelihood estimation to discuss the point estimation of the parameters.

Key Words： Rayleigh-Geometric distribution; Compound extreme value distribution; Properties; Maximum likelihood estimation

隨著壽命分布的深入研究和廣泛應用，國外學者在經典壽命分布的基礎上提出了一些新型的復合分布，Adamidis（1998年）首次提出Exponential-Geometric分布[1]，之后陸續提出了Exponential-Poisson分布、Weibull-Geometric分布、Weibull-Poisson分布、Poisson-Lomax分布、廣義的Exponential-Geometric分布、廣義的Exponential-Poisson分布、互補的Exponential-Geometric分布等，這些文獻定義了新的混合壽命分布，研究其各種性質，得到其參數的極大似然估計，這些研究拓廣了壽命分布的類型。近年來，在極值理論逐步發展的基礎上，國內學者研究了各種復合極值分布及其性質：Poisson-Gumbel分布的參數估計[2]、二項-廣義Pareto分布模型[3]、Pareto- Geometric分布及其性質[4]、二項-Gumbel分布的參數估計[5]、Poisson-Lomax分布的Bayes估計[6]、指數-威布爾分布的貝葉斯估計[7]、兩參數指數商分布的統計分析[8]、三參數Student-t分布的參數估計[9]、四參數Birnbaum-Saunders分布密度函數的圖像特征[10]、泊松-指數混合分布的性質和參數估計[11]等。現在復合極值分布已經廣泛應用于氣象、交通、水文、地震、保險、金融等領域。Rayleigh分布是一種重要的壽命分布，常用在電力和可再生能源這兩個學科。該文通過復合Rayleigh分布和Geometric分布，得到兩參數的新型復合極值分布：Rayleigh-Geometric分布，研究其分布函數、概率密度函數及圖象特征、數字特征等相關性質，并研究分布參數的極大似然估計。

1? Rayleigh-Geometric分布（RG分布）XZ

1.1 分布的定義

帶有尺度參數β（β>0）的Rayleigh分布 Rayleigh（β）的概率密度函數為：

其分布函數為：

Weibull-Geometric分布（WG分布）當形狀參數α=2時的特例就稱為兩參數的Rayleigh-Geometric分布（RG分布）：

定義1? 密度函數為：

或等價地，分布函數為：

此分布稱為Rayleigh-Geometric分布（簡稱RG分布），記為RG（p，β），其中00為參數。

RG（p，β）有兩個參數p和β.對所有參數p和β，當x→∞時，f（x;p，β）→0。當p趨近于0時，RG（p，β）趨近于參數為β的Rayleigh分布Rayleigh（β）。

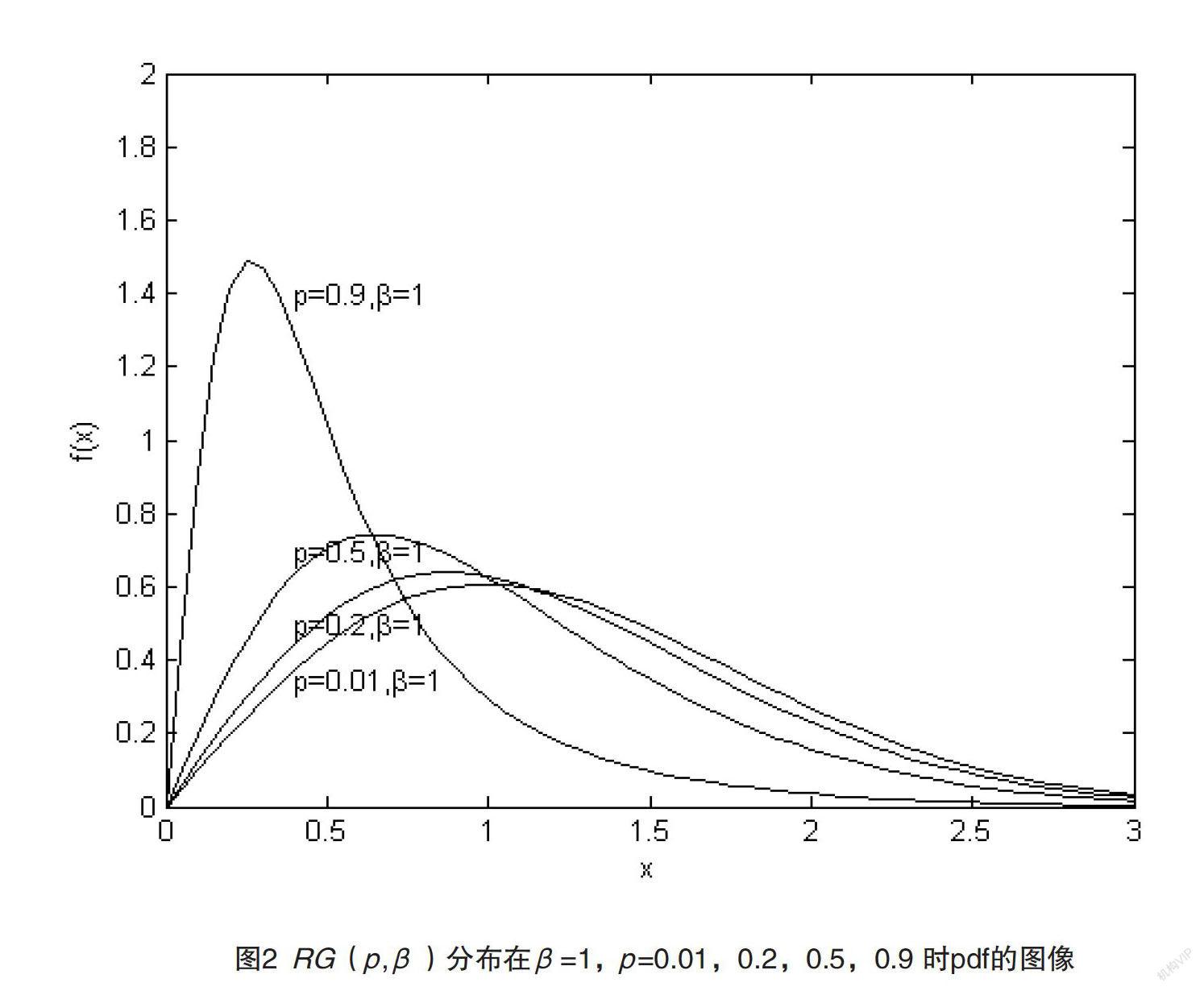
以下給出RG（p，β）的概率密度函數f（x;p，β）在參數的一些特定取值時的圖像，圖1是p=0.5，β=0.5，1，2，3時的概率密度曲線，圖2是β=1，p=0.01，0.2，0.5，0.9時的概率密度曲線。

1.2 分布的性質

定理1 （1）RG（p，β）的眾數在p趨近于0時為β。

（2）對0

證明：由RG（p，β）的定義1.1及分位數、眾數、中位數的定義可得，內容略。

記為歐拉多對數方程[12]。

定理2 （1）RG（p，β）的k階矩：

特別地，RG（p，β）的數學期望：

（2）RG（p，β）的方差：

證明：（1）由于：

當n=2時，有：

由上式及定義1中的密度函數公式（2），當x>1時，

故當k≥1時，有：

（2）RG（p，β）的方差：

證畢。

下面研究RG分布的生存函數和危險率函數，先回顧相關定義。設非負隨機變量X的分布函數為F（x），分布密度為f（x），則其生存函數為S（x）：=1-F（x;p，β），危險率函數為：

定理3RG（p，β）具有如下特性。

（1）生存函數為：

（2）危險率函數為：

并有：

證明：（1）由生存函數的定義及定義1中的分布函數（3），即得。

（2）由危險率函數的定義，定義1中的密度函數，公式（2）及定理3中生存函數的表達式，得：

2? 參數的極大似然估計

從定理2中的RG（p，β）k階矩可以看出，RG（p，β）分布的數學期望的公式結構比較復雜，因此參數的矩估計不易求出，以下用極大似然法來求參數的估計[13]。

從RG分布中抽取容量為n的簡單隨機樣本，記，其似然函數為：

對數似然函數為：

似然方程為：

似然方程的解即是參數p，β的極大似然估計。

參考文獻

[1] ADAMIDIS K，LOUKAS S.A Lifetime Distribution with Decreasing Failure Rate[J]. Statistics and Probability Letters，1998，39（1）：35-42.

[2] 劉晶，吳新榮，李素紅.Poisson-Gumbel復合極值分布的參數估計[J].統計與策，2007（9）：17-19.

[3] 張香云，程維虎.二項-廣義Pareto復合極值分布模型的統計推斷[J].應用數學學報，2012（3）：560-572.

[4] 姚惠，戴勇，謝林.Pareto-Geometric分布[J].數學雜志，2012，32（2）：339-351.

[5] 何曉申，田茂再.二項-Gumbel復合極值分布的參數估計[J].統計與決策，2017，479（11）：17-19.

[6] 張春雨，劉祿勤.定數截尾情形下Poisson-Lomax分布的Bayes估計[J].統計與決策，2018，502（10）：70-73.

[7] 張月.指數Weibull分布的貝葉斯估計與模擬[D].武漢：華中科技大學，2012.