插值法與擬合法在傳染病問題中的應用

楊瑩 閆澤飛 華瑛

DOI：10.16661/j.cnki.1672-3791.2107-5042-7919

摘? 要：該文是針對插值法與擬合法在傳染病問題上的應用分析。搜集連續60天的患病人數作為處理數據，通過使用插值法和擬合法進行模擬，求得累計患病人數與時間的關系。結果表明：（1）在精度上拉格朗日插值法與牛頓插值法的誤差相似。但是對于一些結構復雜的函數，牛頓插值法的優勢比起拉格朗日插值法更加明顯。（2）使用數據擬合法進行傳染病問題的應用分析，相較于插值法處理能得到更加精準的結果。

關鍵詞：拉格朗日插值法? ?牛頓插值法? ?差商? ?數據擬合法? ?最小二乘法

中圖分類號：O314? ? ? ? ? ? ? ? ? ? ? ? ? ?文獻標識碼：A文章編號：1672-3791（2021）08（a）-0183-04

Application of Interpolation Method and Fitting Method in Infectious Disease

YANG Ying? YAN Zefei? HUA Ying*

（College of Information Engineering， Xi'an University， Xi'an， Shaanxi Province， 710065 China）

Abstract： This paper analyzes the application of interpolation method and fitting method in the problem of infectious diseases. The number of patients in 60 consecutive days was collected as the processing data， and the relationship between the cumulative number of patients and time was obtained by using interpolation method and fitting method for simulation. The results show that： （1） The errors of Lagrange interpolation method and Newton interpolation method are similar in accuracy. However， for some functions with complex structure， the advantages of Newton interpolation method are more obvious than Lagrange interpolation method. （2） The application analysis of infectious disease problems using data fitting method can get more accurate results than interpolation method.

Key Words： Lagrange interpolation method; Newton interpolation method; Difference quotient; Data fitting method; Least square method

病毒威脅著人類的健康，所以能夠準確地模擬和預測其傳播情況尤為重要。基于此，我們運用插值法和擬合法分別對病毒的傳播情況進行模擬求解，計算與實際結果之間的誤差，并對誤差產生的原因進行分析。

1? 數據選取與研究方法

1.1 數據選取

依據某傳染病發展的情況[1]，選取連續60天（2020年1月30日至3月20日）的累計患病人數作為處理數據分別進行預測。

1.2 研究方法

1.2.1 插值法

（1）拉格朗日插值法。拉格朗日插值法[2]通過構造插值基函數求解多項式插值函數。基于此構造插值多項式：

（2）牛頓插值法。牛頓插值[3]引入了差商的概念，其插值多項式具有承襲性，函數在點t0，t1，...，tk處的k階差商：

依據差商構造差商表，進而表示牛頓插值多項式中的系數：

于是，可得到滿足插值條件的n次牛頓插值多項式：

1.2.2 數據擬合法

如果涉及到較多數據，使用插值法計算的誤差較大，因此使用數據擬合法[4]求解，依據曲線的函數關系式式，它在處誤差為：

基于最小二乘原理，將總誤差的平方和最小化，使其逼近或擬合已知數據，即：

2? 結果分析

2.1 插值法

2.1.1 拉格朗日插值法

根據數值表使用一次插值法和二次插值法分別求得t=45處的累計確診人數如表1所示，可以得出：二次插值法比一次插值法求得的值更準確，誤差更小。該文猜想是否插值的次數越高，誤差越小。

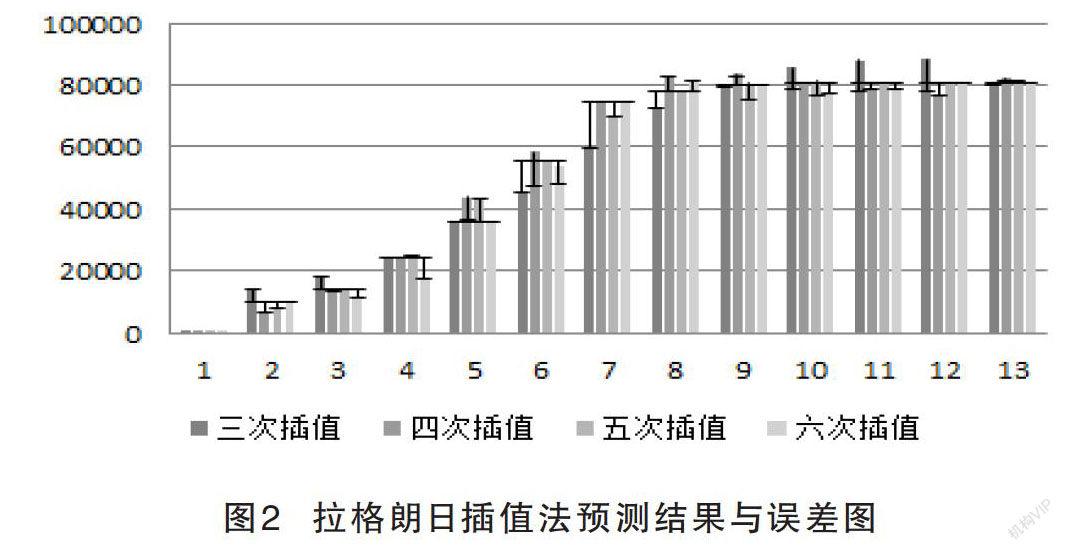
為驗證猜想，進行高次插值[5]，進而得到累計患病人數與時間的變化的函數圖像，再將不同次數預測結果的誤差用圖像描述，見圖1、圖2。通過圖1可以看出：插值次數越高，預測值與實際值的誤差越小，因此，該文猜測是正確的。

通過圖2可以得出以下結論：

（1）隨著插值多項式次數的升高，預測的結果與實際值相比誤差逐漸越小。

（2）傳染病擴散前期和后期誤差比中間要大，出現該現象的原因與病毒的潛伏期有關。

2.1.2 牛頓插值法

為對預測結果的誤差有一個準確的評價，使用牛頓插值法進行求解，繪出預測值與真實值對比圖像見圖3、圖4所示。

通過誤差分析圖可以得出以下結論：

（1）隨著插值多項式次數的升高，預測的結果與實際值相比誤差逐漸減小。

（2）使用三次、四次、五次插值法求得的結果在傳染病擴散后期誤差均比前期要大得多，而使用六次插值該處的誤差大的現象得到了改善。

2.2 擬合法

在插值法的討論過程中，使用拉格朗日插值法計算，會導致病毒擴散前期存在較大的誤差;使用牛頓插值法計算，則會導致病毒擴散后期出現較大的誤差。雖然隨著插值次數的升高，所求的累計患病人數與實際值誤差越小，但是依然存在缺陷。在此基礎下，使用數據擬合法[6]分別對傳染病擴散期間累計確診人數進行擬合求解，圖5為擬合結果。

通過圖像可以得出以下結論：

（1）隨著階數的增高，誤差逐漸減小，這一結論與插值法所求得的結論基本一致。

（2）擬合法求出的擬合值與真實值更加地接近，求得的結果相較于插值法更準確，誤差也明顯地減少。

3? 結語

在對傳染病問題的應用分析中，使用插值法進行求解，低次插值會導致誤差較大，如果要使結果更加準確，就需要進行高次插值求解，這就使得計算量大大增加，缺乏實用價值。而使用數據擬合法，可以避免這個問題，使得數據點在所擬合的曲線附近分布，該曲線能夠更加準確地反映累計確診人數的總體變化趨勢。因此，在科研和生產實踐中，采用數據擬合法對已知點進行擬合，是一種更加實用的方法。

參考文獻

[1] 百度.疫情實時大數據報告[EB/OL].[2021-03-20].https：//voice.baidu.com/act/newpneumonia/newpneumonia/？from=osari_pc_1#tab0.

[2] 郭小樂.基于matlab的常見插值法及其應用[J].赤峰學院學報：自然科學版，2017，33（7）：5-7.

[3] 周建杰，禹仁貴.基于MATLAB軟件的牛頓插值法理論研究[J].河南科技，2018（32）：10-12.

[4] 劉利敏，吳敏麗.基于Matlab的最小二乘曲線擬合[J].福建電腦，2019，35（8）：9-12.

[5] 王玉春，王昆，陽海鵬，等.幾種插值和擬合算法在潮汐插值上的應用分析[J].科技創新導報，2018，15（8）：114-115.

[6] 楊波，于振華，蔡遠利.COVID-19傳播與控制數學建模研究[J/OL].西安交通大學學報：1-10[2021-07-20].http：//kns.cnki.net/kcms/detail/61.1069.t.20210716.1127.008.html.