關(guān)于初中幾何試題的研制對(duì)策探究
郭國(guó)盛 王亞坤

摘 要:初中數(shù)學(xué)是數(shù)學(xué)學(xué)習(xí)的基礎(chǔ),特別初中幾何是初中數(shù)學(xué)的重要部分,對(duì)數(shù)學(xué)技能要求較高。文章對(duì)數(shù)學(xué)能力、技能、焦虛及初中幾何教學(xué)與探索進(jìn)行了論述。通過(guò)幾何教學(xué)的案例及2021年福建省中考幾何綜合試題的解題分析,進(jìn)行初中幾何試題研制及應(yīng)用研究。
關(guān)鍵詞:初中幾何;數(shù)學(xué)能力;數(shù)學(xué)技能;數(shù)學(xué)焦虛
作為初中數(shù)學(xué)老師的我們,已任教多年,談一談初中幾何教學(xué)之我見:
數(shù)學(xué)是一門古老而常新的工具學(xué)科,是研究數(shù)量、結(jié)構(gòu)、變化以及空間模型等概念。數(shù)學(xué)有七大能力,包括:抽象概括能力、空間想象能力、推理論證能力、運(yùn)算求解能力、數(shù)據(jù)處理能力、應(yīng)用意識(shí)、創(chuàng)新意識(shí),其中運(yùn)算能力、邏輯思維能力、空間想象能力是數(shù)學(xué)的三大基本能力。
初中數(shù)學(xué)是數(shù)學(xué)的基礎(chǔ),特別初中幾何是初中數(shù)學(xué)的重要部分,屬于平面幾何,對(duì)數(shù)學(xué)技能要求較高,其中解題過(guò)程經(jīng)常要做好幾條輔助線,遇到解決問(wèn)題困難會(huì)產(chǎn)生“數(shù)學(xué)焦虛”。
數(shù)學(xué)技能是指通過(guò)學(xué)習(xí)而形成的合法則的數(shù)學(xué)活動(dòng)方式,屬于動(dòng)作經(jīng)驗(yàn)。它所要解決的是完成活動(dòng)所要求的動(dòng)作會(huì)不會(huì)與熟不熟練的問(wèn)題,一般分為操作性技能(如使用運(yùn)算工具的技能、測(cè)量技能、作圖技能等)和心智技能(如審題技能、解析技能、運(yùn)算技能、檢驗(yàn)技能等)。
數(shù)學(xué)焦慮是指學(xué)習(xí)數(shù)學(xué)的過(guò)程中產(chǎn)生的一種憂慮等緊張狀態(tài),主要源于對(duì)數(shù)學(xué)的錯(cuò)誤認(rèn)知以及過(guò)去的消極經(jīng)驗(yàn)。實(shí)際教學(xué)中應(yīng)首先從矯正學(xué)生對(duì)數(shù)學(xué)的認(rèn)知偏差入手,并貫穿教材選編、教學(xué)活動(dòng)安排,教學(xué)成效評(píng)估等各方面。
作為數(shù)學(xué)教師具有專業(yè)知識(shí)后,還要學(xué)習(xí)了解最新的學(xué)科研究成果,懂得教育規(guī)律,研究學(xué)生的心理狀況。教學(xué)中還要做到語(yǔ)言幽默和正確運(yùn)用教育理論,關(guān)注教材知識(shí)點(diǎn)的變化與更新,及時(shí)學(xué)習(xí)和掌握新知,充實(shí)豐富本學(xué)科的專業(yè)知識(shí)。
其次,師者,所以傳道授業(yè)解惑也。顧名思義,在數(shù)學(xué)教學(xué)中首先培養(yǎng)學(xué)生對(duì)數(shù)學(xué)感興趣,與學(xué)生打成一片,通過(guò)現(xiàn)實(shí)生活實(shí)例來(lái)學(xué)習(xí)數(shù)學(xué)、研究初中幾何。授課中要循循善誘,給學(xué)生一定的思考時(shí)間,比如以案例一進(jìn)行授課。以北師大七年級(jí)下冊(cè)第四章第3節(jié)第1課時(shí)探索三角形全等條件(SSS)為例:
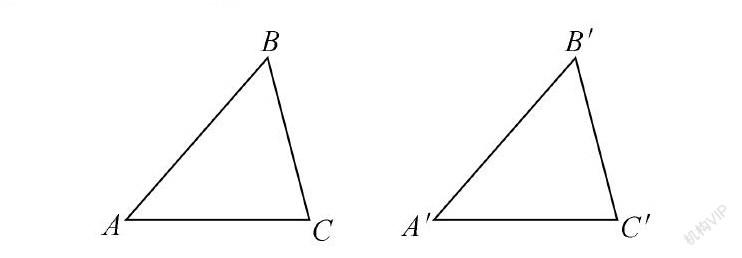
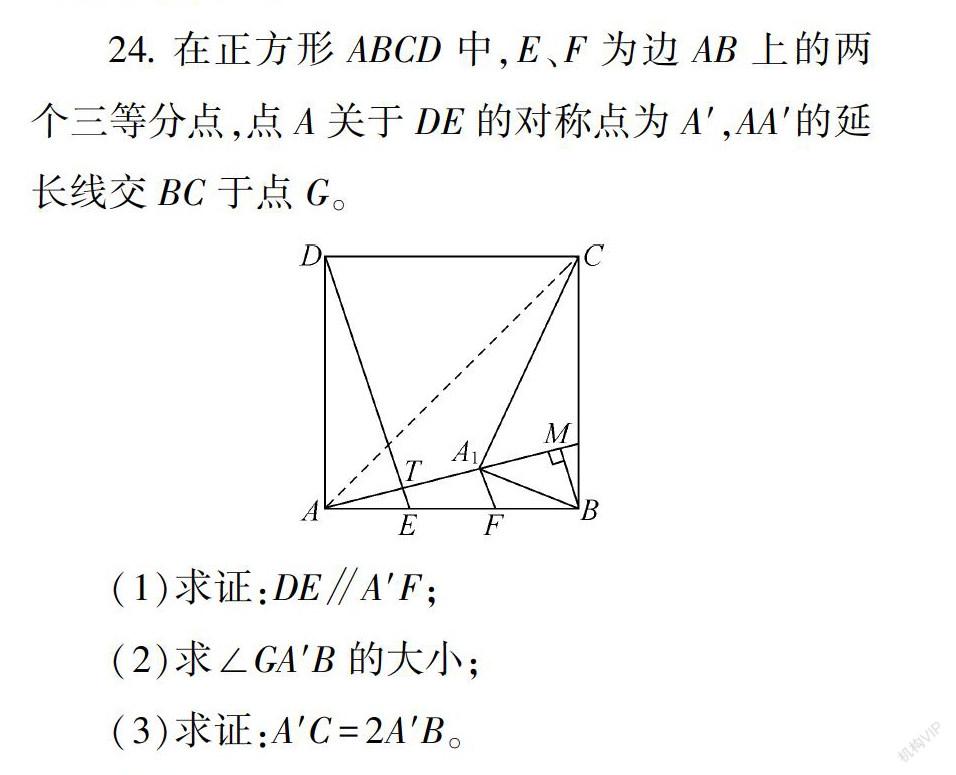
提出幾個(gè)問(wèn)題讓學(xué)生思考并解決。問(wèn)題1:什么是全等圖形?問(wèn)題2:全等三角形有什么性質(zhì)?問(wèn)題3:對(duì)兩個(gè)三角形來(lái)說(shuō),以下六個(gè)條件中至少要滿足幾個(gè)條件,才能確保△ABC≌△A′B′C′呢?
AB=A′B′;BC=B′C′;AC=A′C′;∠A=∠A′;∠B=∠B′;∠C=∠C′。(此處的問(wèn)題設(shè)置非常到位,目標(biāo)精準(zhǔn)明確,有的放矢。)
讓學(xué)生思考幾分鐘并解決問(wèn)題:?jiǎn)栴}1答案:能夠完全重合的兩個(gè)圖形,是全等圖形。問(wèn)題2答案:全等三角形對(duì)應(yīng)角相等,全等三角形對(duì)應(yīng)邊相等。
教師引導(dǎo)探究:?jiǎn)栴}4:?jiǎn)栔辽傩枰獛讉€(gè)條件,我們應(yīng)該從幾個(gè)條件開始探究呢?問(wèn)題5:探究哪個(gè)呢,怎么分類探究呢?問(wèn)題6:只滿足一個(gè)條件時(shí),能否保證兩個(gè)三角形全等?(讓學(xué)生黑板上畫圖演示,加深理解和記憶)問(wèn)題7:接下來(lái)該怎樣探究呢?問(wèn)題8:兩個(gè)條件怎么選取和分類呢?問(wèn)題9:只滿足兩個(gè)條件時(shí),能否保證兩個(gè)三角形全等呢?(讓學(xué)生黑板上畫圖演示,加深理解和記憶)
讓學(xué)生思考幾分鐘并解決問(wèn)題:?jiǎn)栴}4答案:一個(gè)。問(wèn)題5答案:一組角相等或一組邊相等。問(wèn)題6答案:一組角相等或一組邊相等。問(wèn)題7答案:探究只滿足兩個(gè)條件時(shí),能否保證兩個(gè)三角形全等?問(wèn)題8答案:一組角對(duì)應(yīng)相等,一組邊對(duì)應(yīng)相等;兩組角對(duì)應(yīng)相等;兩組邊對(duì)應(yīng)相等。問(wèn)題9答案:不能。
教師引導(dǎo)探究:?jiǎn)栴}10:接下來(lái)該怎樣探究呢?問(wèn)題11:三個(gè)條件怎么選取和分類呢?問(wèn)題12:三組角對(duì)應(yīng)相等兩三角形全等嗎?
讓學(xué)生思考幾分鐘并解決問(wèn)題:?jiǎn)栴}10答案:探究滿足三個(gè)條件時(shí),能否保證兩個(gè)三角形全等?問(wèn)題11答案:三組角對(duì)應(yīng)相等;三組邊對(duì)應(yīng)相等;兩組角對(duì)應(yīng)相等,一組邊對(duì)應(yīng)相等;兩組邊對(duì)應(yīng)相等,一組角對(duì)應(yīng)相等。問(wèn)題12答案:不能。教師:你能舉出反例嗎?學(xué)生:老師的大三角板和學(xué)生的小三角板。
教師引導(dǎo)探究:?jiǎn)栴}13:三組邊對(duì)應(yīng)相等,能否保證兩個(gè)三角形全等?(學(xué)生動(dòng)手實(shí)踐:將課前準(zhǔn)備的小紙條分折成三段長(zhǎng),并將其圍成三角形,并觀察與同桌之間的三角形存在什么樣的關(guān)系。)
最后教師引導(dǎo):1)你能把你的發(fā)現(xiàn)和同學(xué)們分享一下嗎?2)能夠把這一事實(shí)用文字語(yǔ)言準(zhǔn)確描述出來(lái)嗎?學(xué)生回答(教師幫助解決):學(xué)生1:會(huì)全等。學(xué)生2:三邊對(duì)應(yīng)相等的兩個(gè)三角形全等。可簡(jiǎn)寫為“邊邊邊”或“SSS”。
以上是幾何教學(xué)探索過(guò)程。這樣學(xué)生通過(guò)理解后,會(huì)牢固掌握知識(shí)。學(xué)生學(xué)習(xí)數(shù)學(xué)符號(hào)后,教師要求學(xué)生用數(shù)學(xué)符號(hào)表示初中幾何的定理且熟練掌握數(shù)學(xué)符號(hào)表示的內(nèi)容和寫好初中幾何的證明格式。
學(xué)生學(xué)好初中幾何知識(shí)后,要教會(huì)學(xué)生怎么運(yùn)用所學(xué)初中幾何知識(shí)去分析及解決問(wèn)題。以2021年福建省中考試卷第24題的幾何題為例分析如何解決初中幾何問(wèn)題。下面文章從不同的角度來(lái)解析問(wèn)題:
24. 在正方形ABCD中,E、F為邊AB上的兩個(gè)三等分點(diǎn),點(diǎn)A關(guān)于DE的對(duì)稱點(diǎn)為A′,AA′的延長(zhǎng)線交BC于點(diǎn)G。
(1)求證:DE∥A′F;
(2)求∠GA′B的大小;
(3)求證:A′C=2A′B。
方法一:
先分析:(1)根據(jù)已知條件中正方形ABCD可推出四個(gè)角都是直角,四條邊都相等,點(diǎn)A關(guān)于DE的對(duì)稱點(diǎn)為A′,則根據(jù)對(duì)稱的知識(shí)可得DE⊥AA′于點(diǎn)T,AT=A′T;E、F為AB的三等分點(diǎn),則可推出AE=EF=FB,由平行線等分線段性質(zhì)可推出DE∥A′F。
(2)要求∠GA′B的大小,看圖預(yù)測(cè)其角度大約為45度,題中又有好幾個(gè)直角,作BM⊥AG于M(先試下不行再用其他路徑,作輔助線要先用鉛筆畫下,若行不通再更改),若能證明A′M=BM,又由∠A′MB=90°,問(wèn)題就解決了,因?yàn)镈E∥A′F,可證DE∥A′F∥BM,由平行線等分線段性質(zhì)可得AT=TA′=A′M,由證明△DAT≌△ABM可得AT=BM=TA′=A′M,又由∠A′MB=90°可得△A′BM為等腰直角三角形,∠GA′B=45°,則就解決問(wèn)題了。
(3)要證明A′C=2A′B,要運(yùn)用(1)第題和第(2)題的結(jié)論當(dāng)成已知條件來(lái)輔助證明,因?yàn)椤螱A′B=45°,聯(lián)想到正方形的對(duì)角線平分對(duì)角且平分的兩個(gè)角都為45°,就做輔助線連接AC,可證:△TAE≌△MBG則可得∠TAE=∠MBG,則∠CAA′=45°-∠TAE,∠A′BA=∠ABG-∠MBG=90°-45°-∠MBG,則∠CAA′=∠ABA′,其中A′C與A′B分別是△CAA′和△ABA′的兩條邊,△CAA′與△ABA′形狀相似,若能證明△CAA′∽△ABA′且相似比為2,問(wèn)題就解決了。
由(2)的證明可知并設(shè)AT=AA′=A′M=BM=t,則由勾股定理可得,A′B=2t,AB=10t,AC=25t,則利用兩邊成比例且夾角相等的判定,ACAB=25t10t=2,AA′A′B=2t2t=2,又因?yàn)椤螩AA′=∠ABA′,則△CAA′∽△ABA′且相似比為2,∴CA′AA′=ACAB,CA′2t=25t10t,則CA′=22t。又∵A′B=2t,∴CA′=2A′B(解題過(guò)程不寫出來(lái)了)
“橫看成嶺側(cè)成峰,遠(yuǎn)近高地各不同。”分析的角度不同解法就不同,就有方法二(中考試卷的標(biāo)準(zhǔn)答案),解題分析:
第(2)題(如上圖)連接FG,先利用正方形的性質(zhì)證明△DAE≌△ABG,可得AE=BG,又FB=BG可得△FBG是等腰直角三角形,∠GFB=45°,取FG的中點(diǎn)O,連接OA′,OB,在Rt△A′FG和Rt△BFG中,由斜邊上的中線等于斜邊的一半可得OA′=OF=OG=12FG,OB=OF=OG=12FG,則OA′=OF=OG=OB,所以點(diǎn)A′,F(xiàn),B,G都在以FG為直徑的⊙O上,即四點(diǎn)同圓,再利用同弧所對(duì)的圓周角相等可得∠GA′B=∠GFB=45°。
第(3)題設(shè)AB=3b,則AD=BC=3b,AF=2b,AE=BF=b。
由(2)得BG=AE=b,利用三角函數(shù)可求∠BAG=∠A′AF且正切值為13,可得A′FAA′=13,設(shè)A′F=t,則AA′=3t,在Rt△A′AF中,由勾股定理,得AF=10t,則10t=2b,t=10b5,A′F=10b5,在Rt△ABG中,由勾股定理AG=10t。利用兩邊成比例且夾角相等的判定,A′FA′G=BFCG=12,∠A′FB=∠A′GC,可證△A′FB∽△A′GC則A′BA′C=BFCG=12,所以A′C=2A′B。(利用三角函數(shù)、勾股定理和證明△A′FB∽△A′GC相似來(lái)解決問(wèn)題。)
學(xué)生學(xué)習(xí)數(shù)學(xué)的目的是使自己掌握一項(xiàng)技能,為祖國(guó)的建設(shè)做貢獻(xiàn),應(yīng)該滿懷信心奮發(fā)拼搏,為祖國(guó)貢獻(xiàn)自己的力量。我們通過(guò)不斷學(xué)習(xí)、實(shí)踐、反思、總結(jié),形成具有獨(dú)特的教育教學(xué)風(fēng)格,有效提高自己的課堂教學(xué)效率,掌握最新教學(xué)理念和方法,在課堂實(shí)踐中努力提高駕馭課堂能力和親和力,與學(xué)生打成一片,提高反思能力。加強(qiáng)個(gè)人修養(yǎng),提高個(gè)人師德水平,做一個(gè)學(xué)生喜歡,家長(zhǎng)滿意、領(lǐng)導(dǎo)放心的好教師——“三尺講臺(tái),志樹十萬(wàn)英才”。
參考文獻(xiàn):
[1]林崇德,楊治良,黃希庭.心理學(xué)大辭典[M].上海:上海教育出版社,2003.
[2]宋宜樺.韓愈《師說(shuō)》的當(dāng)代教育啟示[J].品位·經(jīng)典,2021(17):9-11+28.
作者簡(jiǎn)介:
郭國(guó)盛,福建省漳州市,漳州臺(tái)商投資區(qū)華僑中學(xué);
王亞坤,福建省廈門市,廈門大學(xué)附屬實(shí)驗(yàn)中學(xué)。

