大數據背景下考慮刪失特點的繼保設備運行狀態評估

張雷，王光華，李金鑠，耿宏賢，戴志輝

(1.國網河北省電力有限公司保定供電分公司，河北 保定 071000；2.華北電力大學電氣與電子工程學院，河北 保定 071003)

0 引言

繼電保護是電力系統的第一道防線，有效利用繼電保護運行數據對繼保設備狀態進行評估，是保持電網安全穩定運行的有效途徑[1—2]。

針對繼保設備的狀態評估，國內外做了大量研究。從繼保設備的原理、硬件、配置等方面進行分析、建模、仿真試驗，然后對其可靠性進行分析，為設備運行狀態評估提供理論依據，也為運維人員提供了提高繼保設備可靠性的方法和策略參考[3—4]。例如文獻[5]詳細介紹了繼保設備可靠性研究現狀和發展趨勢，并指出設備可靠運行是保證電網穩定的重要因素。文獻[6]指出設備本身、信息系統和人為因素是保護系統風險的主要來源，并進一步分析了繼保設備故障風險對一次系統的影響。文獻[7]提出了一種基于變權重模糊綜合評價的繼保設備狀態評價方法，其指標更加完善，但需要足夠多的失效樣本，而繼保設備本身可靠性較高，失效樣本數量較少，因此難以滿足精度要求。對此，文獻[8]在三參數威布爾分布模型的基礎上結合灰色模型，在小樣本條件下對繼保設備進行壽命評估，取得了精度較高的計算結果。文獻[9]從擴充樣本的角度出發，使用蒙特卡洛法進行抽樣，提高了小樣本情況下評估結果的穩定性。文獻[10]考慮了繼保設備缺陷數據的隨機截尾特征，基于兩參數威布爾分布，采用極大似然估計(maximum likelihood estimation，MLE)實現參數估計，但未考慮區間刪失數據的影響。整體上，目前繼保設備運行狀態評估方法很少計及刪失數據的特點，且對包含刪失數據的保護運行“大數據”未充分挖掘，造成了信息損失、可靠性評估結果偏頗和分析模型假設過多的問題。圍繞電力大數據的分析與利用，國內外學者已進行了大量研究[11—12]。但在大數據背景下，對繼保設備的失效數據進行挖掘、分析，從而為判別繼保設備狀態、評估其運行水平提供可行途徑的相關研究，還較少見到。研究基于大數據的繼保設備可靠性分析與運行狀態評估方法具有重要意義。

文中結合繼保設備運行數據特點，首先基于期望-最大化(expectation-maximization，EM)算法對失效模型的參數進行估計，并計算得到設備的可靠性指標；其次，對比各失效期內不同估計方法得到的模型參數精度，驗證了方法處理刪失數據的有效性；最后，通過算例驗證了利用文中方法規劃設備檢修周期的可行性。

1 大數據背景下失效數據特點分析

長期實踐經驗表明，設備失效率與累計運行時間之間的函數關系可用浴盆曲線表示。設備的全壽命周期由早期失效期、偶然失效期與老化失效期組成[13]。對于繼保設備，出廠前會經過充分的測試以排除隱患，現場安裝后，運維人員也會對設備進行嚴密的調試。因此，可認為繼保設備投運后其運行狀態便處于偶然失效期。繼保設備的失效數據一般是在其投入運行之后收集的現場數據。

受觀測條件與監測手段的限制，現場收集到的失效數據可能包含4種類型。

(1)精確數據。繼保設備的自檢功能日益完善，自檢周期非常短，因此自檢發現缺陷的時間即可認為是缺陷發生的準確時間。此外，在周期較短的巡視過程中的缺陷發現時間也可認定是缺陷發生時間。這類失效數據稱為精確數據，如圖1中編號為1、2的失效數據，線段的左端點表示設備的投運時間，右端點表示缺陷發生時間。

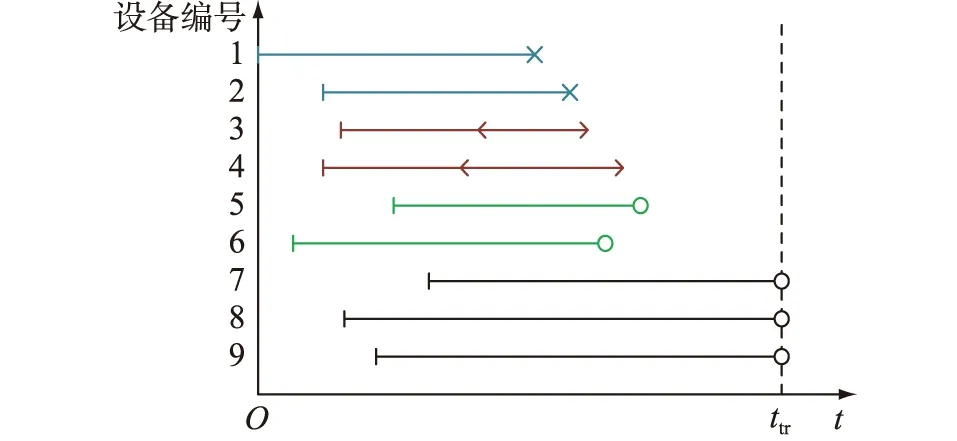
圖1 原始失效數據Fig.1 Raw failure data

(2)區間刪失數據。部分隱蔽性較強的缺陷無法自檢查出，無法確定具體發生時間，如專業巡視時發現的“復歸按鈕脫落”“備用線圈斷線”等缺陷，只可推斷出發生在本次巡視前、最近一次巡視之后。文中稱此類無法確定缺陷發生的確切時間，只能推斷時間區間的失效數據為區間刪失數據。如圖1中編號為3、4的失效數據，線段的左端點表示設備的投運時間，尖括號之間的線段表示缺陷發生時間所在的區間。

(3)右刪失數據。在實際工作情況下收集繼保設備的失效數據，往往伴隨著各種偶然事件。在觀察結束之前，有可能會出現樣本設備中途退出運行的情形。設備在退出運行之前始終保持正常工作，只能得到設備保持正常工作的時長，此類數據稱為右刪失數據。如圖1中編號為5、6的失效數據，線段的左端點表示設備的投運時間，右端點表示設備退出運行的時間。

(4)隨機截尾數據。繼保設備的可靠性水平較高，因此直到觀察結束，大部分設備仍能保持正常工作。此類直至觀察結束仍未出現失效的樣本數據稱為截尾數據[10]，如圖1中編號為7、8、9的失效數據，線段的左端點表示設備的投運時間，右端點表示觀察結束的時間，即截尾時間ttr。

因各繼保設備的投運時間不同，所以當到達ttr時，各繼保設備的運行時間也不盡相同。如果把各樣本設備的投運時刻移動到同一計時起點，這些設備的失效數據將表現出隨機截尾的特點，見圖2。

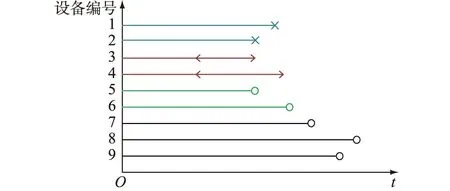
圖2 計時起點對齊后的失效數據Fig.2 Failure data after starting time is aligned

針對繼保設備失效數據的上述特點，常用的最小二乘法等算法已無法滿足設備失效模型參數估計的需求。文中結合EM算法，利用帶有刪失特性的失效數據，估計繼保設備失效模型的參數。

2 繼保設備失效分布模型

失效分布模型能反映設備所處運行階段及設備的運行狀態。采用指數分布模型和威布爾分布模型，通過計算分布模型的參數，估計設備的可靠度R、故障率λ、平均無故障時間tMTBF等指標。其中，指數分布反映偶然失效期的失效特征，常用于擬合具有恒定失效率的設備壽命分布，運行的繼保設備多處于該失效期。威布爾分布則可通過不同的形狀和尺度參數反映早期失效期(失效率遞減)、偶然失效期和損耗失效期(失效率呈加速趨勢，如繼保設備的老化期)特征，具備較強的靈活性。

2.1 指數分布

指數分布模型[14]的可靠性指標如下。

可靠度函數：

R(t)=e-λt

(1)

式中：t為設備失效時間。

故障概率密度函數：

(2)

失效率：

λ(t)=λ

(3)

平均無故障時間：

tMTBF=1/λ

(4)

2.2 威布爾分布

威布爾分布模型[15—17]可分成三參數和兩參數2種形式。兩參數模型的函數表達式如下。

可靠度函數：

R(t)=e-(t/η)k

(5)

式中：η>0為尺度參數；k>0為形狀參數。

故障概率密度函數：

(6)

失效率：

λ(t)=(k/η)(t/η)k-1

(7)

平均無故障時間：

tMTBF=ηΓ(1+1/k)

(8)

式中：Γ(·)為伽馬函數。

3 繼保設備運行狀態評估

3.1 EM算法

EM算法的基本思想是：當失效數據樣本中存在刪失數據時，若已知分布模型的參數，則可以結合已知樣本數據估計刪失數據的數學期望。反之，若已知刪失數據的值，則可利用MLE估計分布模型的參數[18]。

EM算法流程簡述如下。(1)輸入包括刪失數據的樣本數據；(2)對分布模型的參數賦初值，并設定可接受的最大參數估計誤差；(3)執行E步：將上次迭代得到的參數估計結果代入分布模型，估計刪失數據的概率分布，并計算刪失數據服從此概率分布下對數似然函數的數學期望；(4)執行M步：對參數尋優，使上述期望達到最大，將尋優結果作為本次參數估計的結果并計算估計誤差；(5)若參數估計誤差小于可接受的最大誤差，計算結束，否則返回步驟(3)。

3.2 基于EM算法的指數分布(EM-exp)模型參數估計

指數分布的故障概率密度函數如式(2)所示，其對數似然函數的數學期望為：

(9)

式中：n為樣本總數；ti為第i個樣本的真實失效時間；z為發生數據刪失的樣本集；θ，θ′分別為不同分布模型中本次和上次迭代得到的參數；對指數分布，λ′，λ分別為上次和本次估計的故障率參數；Q(·)為似然函數的數學期望；E(·)為ti在服從上次估計的故障率參數下對數似然函數的數學期望。

當Q(θ|θ′)取得極大值時，有：

(10)

根據EM算法的收斂性質，當迭代次數ω→+∞時，λ收斂于定值，即：

λ=λ′ω→+∞

(11)

迭代次數足夠多時，將式(10)中的各數學期望項展開，并將式(11)代入式(10)，得：

(12)

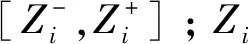
采用數值方法求解上述方程即可得到指數分布模型的參數估計值。

3.3 基于EM算法的威布爾分布(EM-wbl)模型參數估計

威布爾分布的故障概率密度函數如式(6)所示。為簡化計算，令μ=1/ηk，則式(6)可改寫為：

(13)

威布爾分布模型對數似然函數的數學期望為：

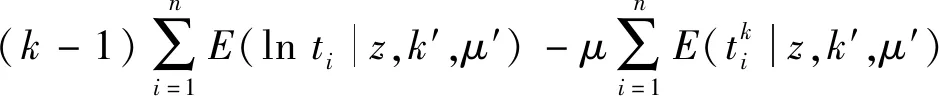
(14)

式中：k′,μ′分別為上次迭代所得威布爾分布的形狀參數和尺度參數估計結果；k,μ為本次迭代估計的參數。

當Q(θ|θ′)取得極大值時，有：

(15)

(16)

當迭代次數ω→+∞時，參數k,μ將收斂于定值，即：

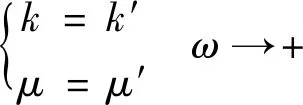
(17)

迭代次數足夠多時，將式(15)、式(16)中的各數學期望項展開，并將式(17)代入式(15)、式(16)，得：

(18)

(19)

求解上述隱函數方程組，即可求得威布爾分布參數k,μ的數值解。

傳統MLE在處理刪失數據時只計及了隨機截尾數據，不能處理區間刪失數據，會影響繼保設備運行狀態評估的準確性。而基于EM算法的失效分布模型，在考慮區間刪失數據的基礎上，可通過對刪失數據的還原處理，得到理想的參數估計值并據此計算設備的可靠度、故障率、平均無故障時間等指標，從而實現繼保設備運行狀態的評估。

4 算例分析

為檢驗模型的正確性，利用計算機生成帶有刪失特性的失效數據進行分析。首先，使用蒙特卡羅法生成服從指數分布和威布爾分布的精確失效數據[19—21]，并以此為基礎生成帶有刪失特性的樣本集。為模擬區間刪失數據，隨機選取部分樣本進行刪失處理。在失效數據的左右兩側分別擴充出刪失區間，兩側的刪失區間長度服從參數為ζ2,σ2的正態分布，且相互獨立。

為模擬右刪失數據，在非區間刪失樣本中隨機選取部分樣本數據，令其刪失時間tc服從(t0,ttr)上的均勻分布，若刪失發生在失效之后，則重新分配小于失效時間的tc。其中，t0為投運時間。

為模擬失效數據的隨機截尾特征，令計時起點為t0=0，各樣本設備的投運時間服從參數為ζ1,σ1的正態分布。若設備的投運時間在計時起點之前，則重新分配大于t0的投運時間。失效時間大于ttr的樣本數據即為截尾數據。

4.1 偶然失效區

繼保設備工作于偶然失效期時，其失效率基本保持不變。使用計算機生成服從指數分布的失效數據，樣本容量為100。生成失效數據時所用參數如表1所示。

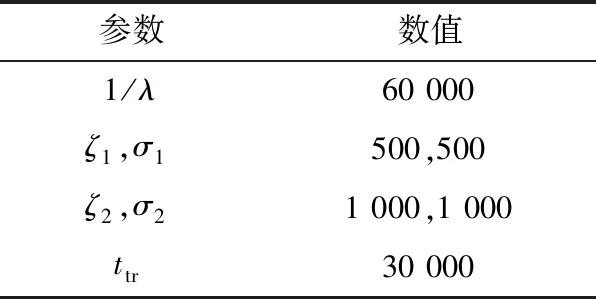
表1 參數表(偶然失效期)Table 1 Parameters table (random failure)

分別使用EM-exp模型、EM-wbl模型和傳統基于MLE的指數分布模型(MLE-exp)進行參數估計。由于MLE-exp方法不能處理區間刪失數據，所以在使用此類數據時，選取缺陷發現時間，即刪失區間的右端點作為設備的失效時間。參數估計結果如表2所示，表中p1為使用計算機生成數據時，精確數據在所有非截尾數據中所占比例；p2為區間刪失數據所占比例；p3為右刪失數據所占比例；tcal為計算耗時。

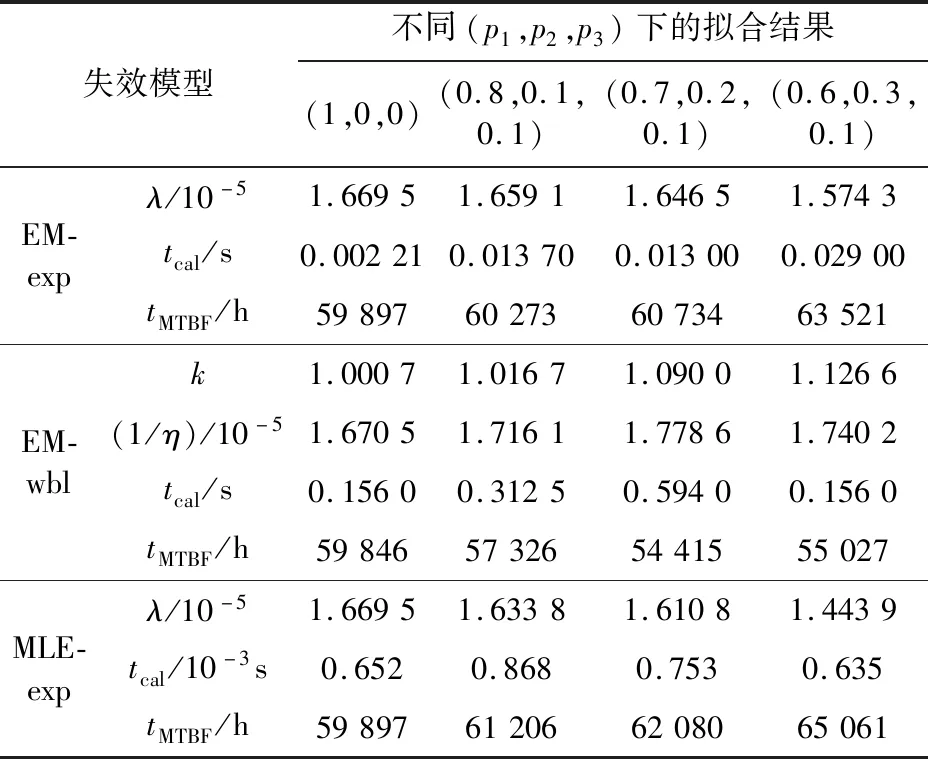
表2 偶然失效區參數擬合結果Table 2 Parameter titting results of random failures

由表2可得：

(1)刪失數據所占比例較小時，與EM-exp模型相比，MLE-exp模型的參數估計耗時最少，且2種模型得到的λ的估計值與真值之間的差距較小。因此，對于失效數據為精確數據的繼保設備，宜采用MLE-exp模型進行參數估計。

(2)隨著刪失數據增多，3種模型得到的參數估計值與真值之間的差距不斷增大，此時EM-exp模型準確性最好。因此，對于失效數據中含刪失數據的繼保設備，宜采用EM-exp模型進行參數估計。

(3)對處于偶然失效期的設備，EM-wbl模型的參數估計結果精度較差。因此，對于具有恒定失效率或定期維護的繼保設備，宜采用EM-exp模型進行參數估計。

4.2 損耗失效區

使用計算機生成服從威布爾分布的失效數據，樣本容量為100。生成數據時所用參數，如表3所示。

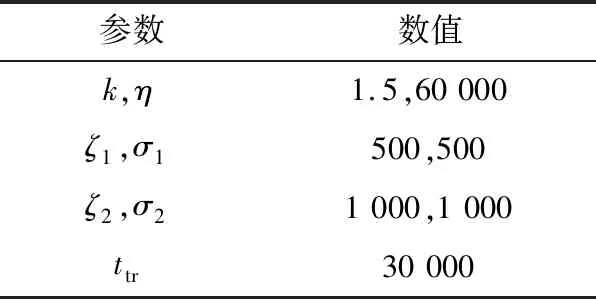
表3 參數表(損耗失效區)Table 3 Parameters table (wearout failure)

指數分布模型不適用于失效率隨時間不斷變化的情形，所以本節只討論威布爾分布模型的參數估計精度。分別使用EM-wbl模型和傳統的基于MLE的威布爾分布模型(MLE-wbl)進行參數估計，估計結果如表4所示。

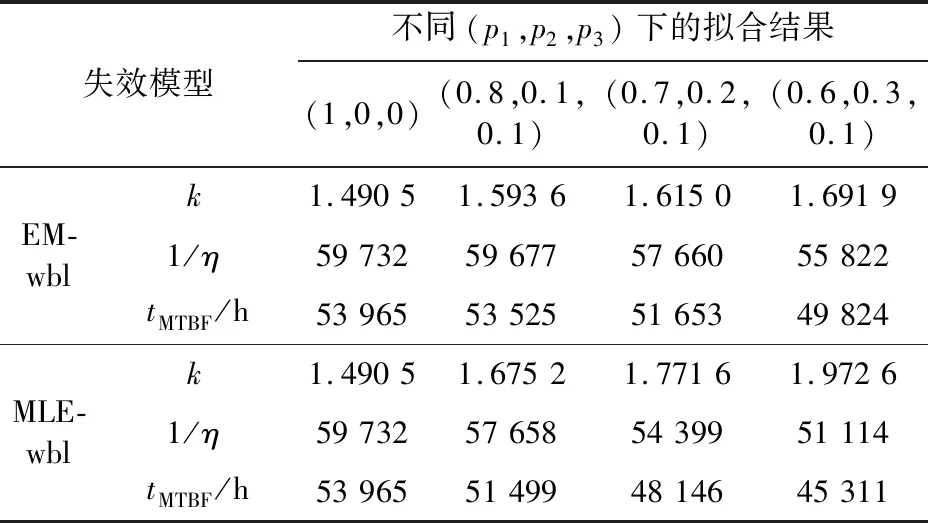
表4 損耗失效區參數擬合結果Table 4 Parameter fitting results of wearout failures

由表4可知，當樣本數據全為精確數據時，2種方法計算得到的參數k,η以及tMTBF的值均相同。隨著刪失數據所占比例不斷上升，2種方法的估計誤差均有所增加，但EM-wbl模型的估計結果更接近準確值，準確度更高。

5 實例分析

5.1 數據預處理

選取某市同一型號的繼保設備50臺，記設備投運時間為t0，停止觀察的時間為截尾時間ttr[22—23]。對于直到觀察結束仍未發生缺陷的設備，其累計運行時長tacc為：

tacc=ttr-t0

(20)

對于沒有發生故障，但在觀察期間退出運行的設備，記其停運時間為tc，其累計運行時長為：

tacc=tc-t0

(21)

對于發生缺陷的設備，若缺陷發現方式為自檢，則發現缺陷的時間即為缺陷發生時間tf，設備的失效時間記為：

t=tf-t0

(22)

若發現缺陷的方式為巡視過程，則設備的失效時間區間(t-,t+)的計算方法為：

(23)

式中：T為設備歷次巡視時間，取其中距缺陷發現時間最近的一次巡視時間作為設備失效區間的左端點，缺陷發現時間為失效區間的右端點。

整理后的部分失效數據如表5所示，觀察期間，50臺設備中共有9臺發生失效，6臺設備的失效時間為精確數據，3臺設備的失效時間為區間刪失數據，無設備在正常運行情況下中途退出運行。

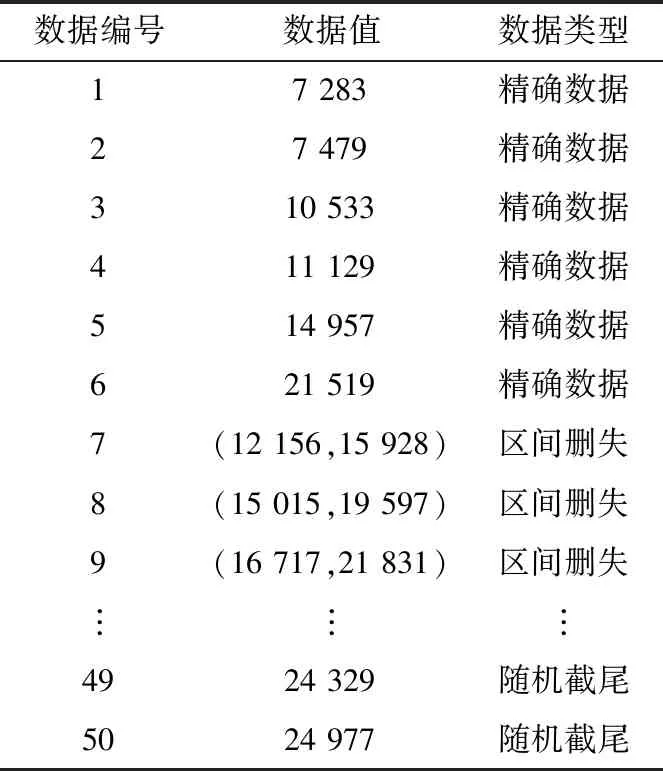
表5 繼保設備失效數據Table 5 Failure data of relay protection equipment

5.2 計算分析

將經預處理的失效數據代入EM-wbl模型中，得到的參數估計值為：

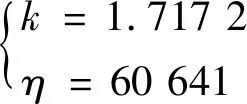
(24)

將參數值代入失效模型中，可得出此型號繼保設備的可靠性指標如下。

可靠度：

R(t)=e-(t/60 641)1.717 2

(25)

故障概率密度：

f(t)=1.050 6×10-8t0.717 2e-(t/60 641)1.717 2

(26)

失效率：

λ(t)=1.050 6×10-8t0.717 2

(27)

平均無故障時間：

tMTBF=54 071

(28)

可靠度、故障概率密度、失效率隨時間變化的曲線如圖3—圖5所示。

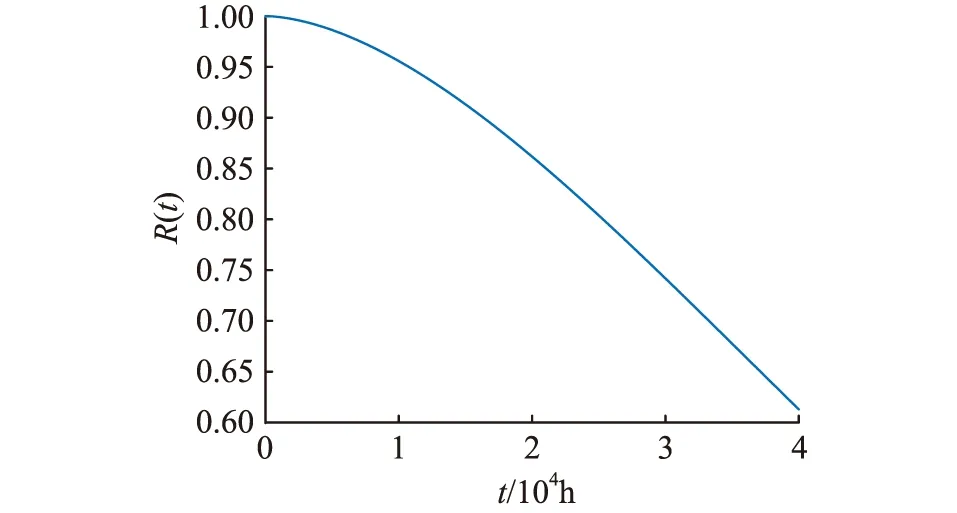
圖3 可靠度曲線Fig.3 Reliability function curve

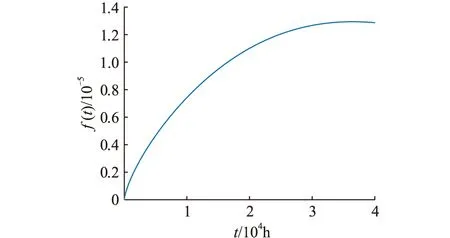
圖4 故障概率密度曲線Fig.4 Fault probability density curve

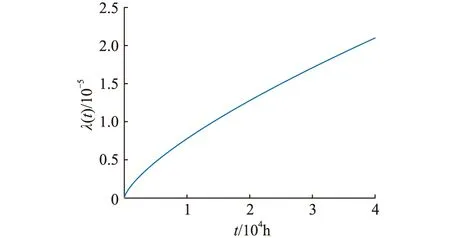
圖5 失效率曲線Fig.5 Failure rate curve

如圖3所示，當R(t)=0.98時，得到繼保設備運行時間為6 250 h，實際運行情況中設備首次失效時間為7 283 h，即通過EM算法得到的參數估計值可以很好的擬合設備可靠度曲線。形狀參數k>1，由圖4、圖5可知，故障概率密度及失效率隨運行時間的增加逐漸增大，反映了繼保設備處于損耗期的特征。平均無故障時間tMTBF可用于檢修周期制定，通常情況下狀態檢修周期Tm=0.1tMTBF，即建議狀態檢修周期為5 407 h。

綜上可知，當存在刪失數據時，采用EM-wbl得到的參數估計值可更精確地擬合設備實際的失效情況，再根據繼保設備可靠度、失效率、故障概率密度等指標隨時間變化的曲線預判其壽命分布，達到評價繼保設備運行水平，預測設備運行年限的目的。

此外，上述分析的失效數據來自同類型設備，因此得出的結論適用于該類型設備。但所提模型對不同型號設備具有普適性。

6 結語

首先分析了繼保設備失效數據的特點，總結了現場收集到的失效數據類型：精確數據、區間刪失數據、右刪失數據和隨機截尾數據。然后在失效數據樣本包含刪失數據的情況下，對比分析了偶然失效期和老化失效期內不同估計方法得到的模型參數精度。證明在偶然失效期內，EM-exp模型得到的參數估計精度更高；在老化失效期內，EM-wbl模型能以更高的精度擬合繼保設備的失效特性曲線。

最后通過對某型號設備數據處理，結合失效分布模型，分析了該繼保設備可靠度、失效率、故障概率密度等可靠性指標的時變特征。利用設備可靠度曲線，可提前判斷設備可靠度，降低到閥值所需的時間，并及時發出告警提醒工作人員加強巡視。利用失效率曲線，可得設備的故障風險隨時間變化的規律，用于安排檢修計劃。利用故障概率密度曲線，可計算設備的平均無故障時間，為合理安排服役年限提供參考。下一步將針對不同類型刪失數據，對比研究不同算法的參數估計精度。